Obliczanie proporcji w matematyce jest kluczowym narzędziem, które pozwala na zrozumienie relacji między różnymi wartościami. Dzięki proporcjom możemy analizować i porównywać dane, co jest niezwykle przydatne w wielu dziedzinach, od matematyki po codzienne życie. Proporcje pomagają w rozwiązywaniu problemów, takich jak obliczanie długości boków podobnych figur w geometrii czy dostosowywanie ilości składników w przepisach kulinarnych.
W tym artykule przedstawimy proste metody obliczania proporcji oraz praktyczne przykłady ich zastosowania. Dowiesz się, jak korzystać z wzorów do obliczania brakujących wartości oraz jak unikać typowych błędów przy rozwiązywaniu zadań z proporcją. Niezależnie od tego, czy jesteś uczniem, studentem, czy po prostu chcesz poprawić swoje umiejętności matematyczne, ten artykuł dostarczy Ci niezbędnych informacji.Najważniejsze informacje:
- Proporcja to równość dwóch ilorazów, co pozwala na porównywanie wartości.
- Wzory do obliczania proporcji umożliwiają wyznaczanie brakujących wartości w zestawach danych.
- Metoda krzyżowego mnożenia jest skutecznym narzędziem do rozwiązywania zadań z proporcją.
- Proporcje mają zastosowanie w matematyce, geometrii, gotowaniu, zarządzaniu budżetem i wielu innych dziedzinach.
- Unikanie typowych błędów przy obliczeniach proporcji jest kluczowe dla uzyskania poprawnych wyników.
Jak obliczać proporcje w matematyce: podstawowe metody i zasady
Obliczanie proporcji w matematyce to kluczowe narzędzie do analizy relacji między różnymi wartościami. Proporcja definiuje się jako równość dwóch ilorazów, co można zapisać jako $$a:b = c:d$$. W tym zapisie $$a$$ i $$d$$ to wyrazy skrajne, a $$b$$ i $$c$$ to wyrazy środkowe. Kluczową właściwością proporcji jest to, że iloczyn wyrazów skrajnych jest równy iloczynowi wyrazów środkowych, co można zapisać matematycznie jako $$a \times d = b \times c$$. Dzięki temu, obliczanie proporcji staje się prostsze, a zrozumienie relacji między wartościami bardziej przejrzyste.
Podstawowe zasady obliczania proporcji obejmują zarówno zrozumienie definicji, jak i umiejętność stosowania wzorów do obliczeń. Aby znaleźć brakującą wartość w proporcji, można zastosować wzory takie jak $$d = \frac{b \times c}{a}$$, gdy znane są wartości $$a$$, $$b$$ i $$c$$. Warto również wspomnieć o metodzie krzyżowego mnożenia, która jest powszechnie stosowana do rozwiązywania równań proporcjonalnych. Ta technika pozwala na szybkie i efektywne obliczenia, co czyni ją niezwykle użyteczną w praktycznych zastosowaniach matematycznych.
Zrozumienie pojęcia proporcji i jej zastosowania w matematyce
Proporcje mają ogromne znaczenie w matematyce, ponieważ umożliwiają porównywanie wartości oraz zrozumienie ich relacji. Dzięki nim możemy analizować dane i wyciągać wnioski w różnych dziedzinach, takich jak geometria, algebra czy statystyka. Proporcje są również kluczowe w naukach przyrodniczych, gdzie pomagają w zrozumieniu zjawisk naturalnych i ich wzajemnych powiązań.
W matematyce proporcje są stosowane nie tylko w teorii, ale także w praktyce. Na przykład, w geometrii służą do obliczania długości boków podobnych figur, a w algebrze ułatwiają rozwiązywanie równań. W codziennym życiu proporcje są niezwykle przydatne, na przykład w gotowaniu, gdzie pozwalają na dostosowanie ilości składników do wielkości porcji, czy w zarządzaniu budżetem, gdzie pomagają w obliczaniu wydatków i oszczędności.Wzory do obliczania proporcji: krok po kroku
Obliczanie proporcji w matematyce opiera się na kilku kluczowych wzorach, które umożliwiają wyznaczanie brakujących wartości. Najczęściej stosowane formuły to $$d = \frac{b \times c}{a}$$ oraz $$a = \frac{c \times d}{b}$$. Te wzory są niezwykle przydatne, gdy znamy trzy z czterech wartości w proporcji i chcemy obliczyć czwartą. Dzięki tym wzorom możemy szybko i efektywnie rozwiązywać zadania dotyczące proporcji, co jest szczególnie ważne w praktycznych zastosowaniach matematycznych.
Aby skutecznie obliczać proporcje, warto stosować się do poniższych kroków:
- Krok 1: Zidentyfikuj znane wartości w proporcji i zapisz je w odpowiednich miejscach (a, b, c, d).
- Krok 2: Wybierz odpowiedni wzór w zależności od tego, którą wartość chcesz obliczyć.
- Krok 3: Podstaw znane wartości do wzoru.
- Krok 4: Wykonaj obliczenia, stosując zasady arytmetyki.
- Krok 5: Sprawdź wyniki, aby upewnić się, że są logiczne i zgodne z danymi.
Obliczanie proporcji w geometrii: długości i podobieństwo figur
W geometrii, proporcje odgrywają kluczową rolę w zrozumieniu podobieństwa figur. Dwie figury są podobne, gdy mają tę samą formę, ale różnią się rozmiarem. Oznacza to, że odpowiadające sobie boki tych figur są w stałej proporcji. Na przykład, jeśli jeden trójkąt ma boki o długości 3 cm, 4 cm i 5 cm, a drugi trójkąt ma boki o długości 6 cm, 8 cm i 10 cm, to te figury są podobne, ponieważ długości ich boków są w tej samej proporcji 1:2. Dzięki tej właściwości możemy łatwo obliczać brakujące długości boków, znając tylko jedną z figur.
Do obliczania proporcji w kontekście podobieństwa figur, możemy zastosować następujące kroki. Po pierwsze, ustalamy proporcję między długościami odpowiadających sobie boków. Następnie, wykorzystując tę proporcję, możemy obliczyć brakujące długości. Na przykład, jeśli znamy długości jednego boku w większej figurze i odpowiadający mu bok w mniejszej figurze, możemy łatwo znaleźć brakujące długości pozostałych boków. Poniższa tabela ilustruje przykład podobieństwa figur z rzeczywistymi wymiarami:
| Figura | Bok 1 (cm) | Bok 2 (cm) | Bok 3 (cm) |
| Trójkąt A | 3 | 4 | 5 |
| Trójkąt B | 6 | 8 | 10 |
Proporcje w codziennym życiu: zastosowanie w gotowaniu i budżecie
Proporcje są niezwykle przydatne w codziennym życiu, zwłaszcza w takich dziedzinach jak gotowanie i zarządzanie budżetem. W kuchni, proporcje pozwalają na dostosowanie ilości składników w przepisach w zależności od liczby porcji. Na przykład, jeśli przepis na ciasto wymaga 200 g mąki na 4 porcje, a chcemy przygotować 8 porcji, wystarczy podwoić ilość mąki do 400 g. Dzięki temu, nie tylko uzyskamy odpowiednią ilość ciasta, ale także zachowamy właściwy smak i konsystencję.
W zarządzaniu budżetem, proporcje pomagają w obliczaniu wydatków i oszczędności. Na przykład, jeśli planujesz wydać 30% swojego budżetu na jedzenie, a Twój miesięczny budżet wynosi 3000 zł, wystarczy pomnożyć 3000 zł przez 0,30, aby uzyskać kwotę 900 zł, którą możesz przeznaczyć na zakupy spożywcze. Umożliwia to lepsze planowanie finansów i unikanie nieprzewidzianych wydatków.
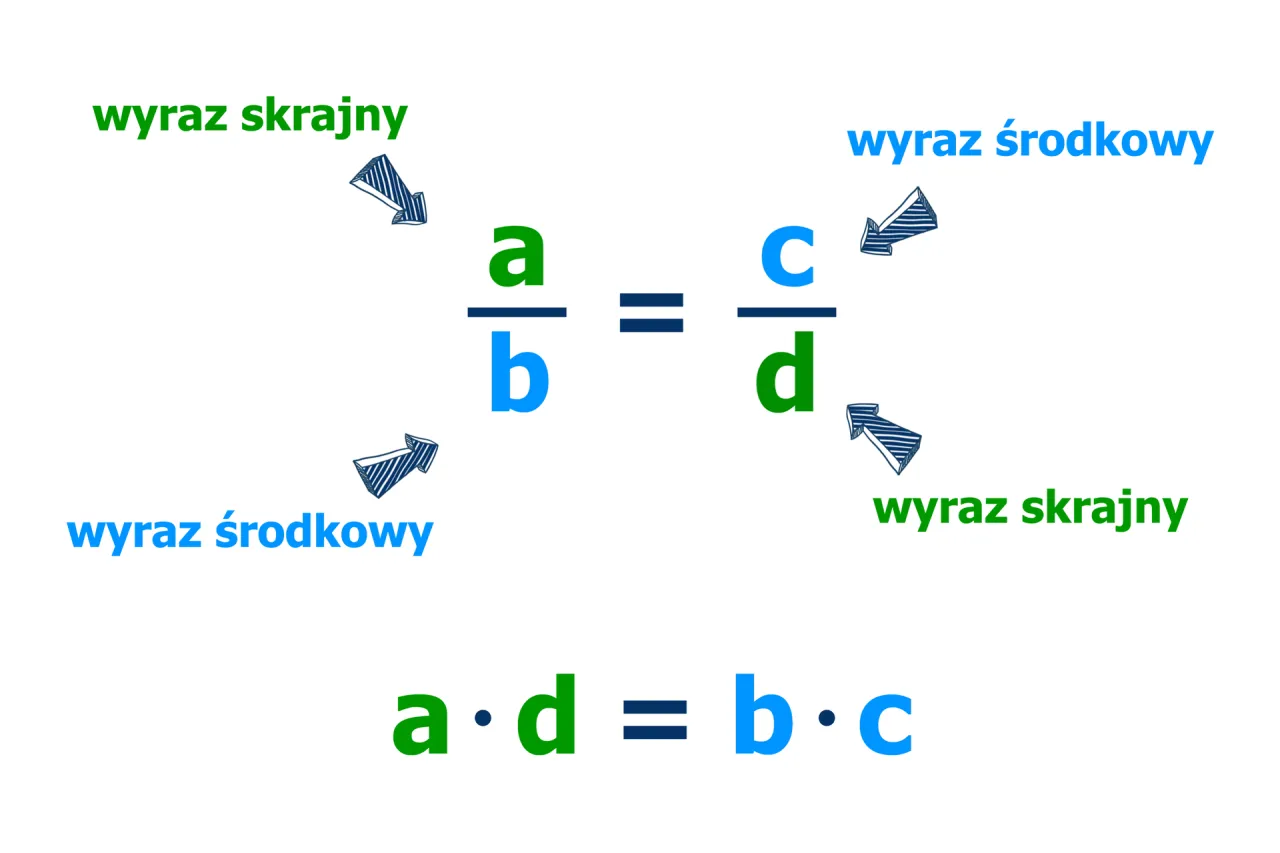
Rozwiązywanie zadań z proporcją: techniki i strategie
Rozwiązywanie zadań z proporcją wymaga znajomości różnych technik i strategii, które mogą ułatwić proces obliczeń. Jedną z najczęściej stosowanych metod jest krzyżowe mnożenie, które polega na pomnożeniu wyrazów skrajnych i środkowych w proporcji. Inną popularną techniką jest stosowanie wzorów, które pozwalają na szybkie wyznaczenie brakujących wartości. Ważne jest również, aby zrozumieć, jak przekształcać proporcje w równania, co może pomóc w ich rozwiązywaniu. Używanie diagramów lub rysunków może również pomóc w wizualizacji problemu, co ułatwia jego rozwiązanie.
Jednak podczas rozwiązywania zadań z proporcją można napotkać różne pułapki i błędy. Często zdarza się, że osoby rozwiązujące zadania mylą wartości skrajne z środkowymi, co prowadzi do błędnych wyników. Inny powszechny błąd to niepoprawne przekształcanie jednostek, co również może wpływać na końcowe obliczenia. Aby uniknąć tych problemów, warto zawsze dokładnie sprawdzić, jakie wartości są używane w obliczeniach oraz upewnić się, że wszystkie jednostki są zgodne. Dobrą praktyką jest również podwójne sprawdzenie wyników, aby upewnić się, że są one logiczne i zgodne z danymi wejściowymi.
Metoda krzyżowego mnożenia: jak ułatwia obliczenia
Metoda krzyżowego mnożenia to jedna z najprostszych i najbardziej efektywnych technik rozwiązywania zadań z proporcją. Polega ona na pomnożeniu wyrazów skrajnych oraz wyrazów środkowych w proporcji. Na przykład, w proporcji $$\frac{a}{b} = \frac{c}{d}$$, możemy obliczyć, że $$a \times d = b \times c$$. Dzięki temu, zamiast rozwiązywać równania z wieloma krokami, możemy szybko przejść do obliczeń, co znacznie przyspiesza proces. Metoda ta jest szczególnie przydatna w sytuacjach, gdy mamy do czynienia z dużymi liczbami lub złożonymi proporcjami.
Korzyści płynące z zastosowania metody krzyżowego mnożenia są liczne. Po pierwsze, jest to technika bardzo intuicyjna, która nie wymaga zaawansowanej wiedzy matematycznej. Po drugie, pozwala na szybkie i dokładne obliczenia, co jest niezwykle ważne w zadaniach czasowych, takich jak egzaminy. Dodatkowo, metoda ta pozwala na łatwe przekształcanie proporcji w równania, co może być przydatne w bardziej skomplikowanych problemach matematycznych. W rezultacie, krzyżowe mnożenie jest nie tylko skuteczne, ale także praktyczne w codziennym obliczaniu proporcji.
Typowe błędy w obliczaniu proporcji i jak ich unikać
Podczas obliczania proporcji w matematyce mogą wystąpić różne typowe błędy, które prowadzą do niepoprawnych wyników. Jednym z najczęstszych błędów jest mylenie wyrazów skrajnych z wyrazami środkowymi, co może skutkować błędnymi obliczeniami. Inny powszechny problem to nieprawidłowe przekształcanie jednostek, co może prowadzić do całkowitych nieporozumień w wynikach. Często zdarza się również, że osoby rozwiązujące zadania nie sprawdzają, czy proporcje są poprawnie ustawione przed przystąpieniem do obliczeń, co może prowadzić do pomyłek. Wreszcie, pomijanie kroków w obliczeniach lub ich nieodpowiednie wykonywanie może również prowadzić do błędów.
Aby uniknąć tych typowych błędów, warto stosować kilka prostych strategii. Po pierwsze, zawsze upewnij się, że rozumiesz, które wartości są skrajne, a które środkowe, zanim przystąpisz do obliczeń. Po drugie, zwracaj uwagę na jednostki miary i upewnij się, że są one zgodne w całym zadaniu. Dobrą praktyką jest również zapisywanie kroków obliczeń, co pozwala na łatwiejsze śledzenie i weryfikację wyników. Na koniec, zawsze warto podwójnie sprawdzić swoje obliczenia, aby upewnić się, że są one logiczne i zgodne z danymi wejściowymi. Dzięki tym wskazówkom można znacznie zredukować ryzyko popełnienia błędów w obliczaniu proporcji.
Jak wykorzystać proporcje w analizie danych i statystyce
Proporcje odgrywają kluczową rolę nie tylko w matematyce, ale również w analizie danych i statystyce. W kontekście analizy danych, umiejętność obliczania proporcji pozwala na identyfikację trendów i wzorców w dużych zbiorach danych. Na przykład, w badaniach rynkowych, proporcje mogą być używane do analizy preferencji klientów, gdzie można obliczyć, jaki odsetek klientów preferuje dany produkt w porównaniu do innych. Tego rodzaju analizy pomagają firmom w podejmowaniu lepszych decyzji strategicznych.
W przyszłości, z rosnącą ilością danych generowanych przez technologie, zastosowanie proporcji będzie jeszcze bardziej istotne. W uczeniu maszynowym i sztucznej inteligencji, proporcje mogą być wykorzystane do oceniania skuteczności algorytmów, a także do optymalizacji modeli predykcyjnych. W miarę jak analityka danych staje się coraz bardziej złożona, umiejętność efektywnego obliczania i interpretowania proporcji stanie się niezbędna dla specjalistów w tej dziedzinie. Warto zatem rozwijać te umiejętności, aby lepiej radzić sobie w dynamicznie zmieniającym się świecie danych.

