Logarytmy to niezwykle ważny temat w matematyce, który pozwala na zrozumienie relacji między potęgami a ich wykładnikami. Aby obliczyć logarytm, musimy znaleźć potęgę, do której należy podnieść podstawę logarytmu, aby uzyskać daną liczbę. Proces ten można zrealizować na kilka sposobów, zarówno ręcznie, jak i za pomocą kalkulatora. W tym artykule przedstawimy różne metody obliczania logarytmów oraz praktyczne przykłady, które pomogą w zrozumieniu tego zagadnienia.
Logarytmy mają zastosowanie w wielu dziedzinach, od nauk ścisłych po inżynierię i finanse. Zrozumienie ich działania jest kluczowe dla rozwiązywania złożonych problemów matematycznych oraz analizy danych. W kolejnych częściach artykułu omówimy, jak obliczać logarytmy, jakie są najczęstsze błędy oraz jak wizualizacje mogą wspierać naukę tego zagadnienia.Kluczowe wnioski:
- Logarytm $$\log_{a}b$$ oznacza wykładnik $$x$$, dla którego $$a^x = b$$.
- Obliczanie logarytmów można przeprowadzać ręcznie lub przy użyciu kalkulatorów.
- Logarytmy są istotne w różnych dziedzinach, takich jak nauka, inżynieria i finanse.
- Typowe błędy w obliczeniach logarytmicznych obejmują nieprawidłowe interpretacje podstawy i wartości logarytmowanej.
- Wizualizacje, takie jak wykresy, mogą znacznie ułatwić zrozumienie logarytmów i ich właściwości.
Definicja logarytmu i jego znaczenie w matematyce
Logarytmy są kluczowym pojęciem w matematyce, które pozwala na zrozumienie relacji między potęgami a ich wykładnikami. Wartością logarytmu $$\log_{a}b$$ jest wykładnik $$x$$, dla którego zachodzi równość $$a^x = b$$. Dzięki tej definicji, logarytmy umożliwiają przekształcanie złożonych równań potęgowych w prostsze formy, co jest niezwykle przydatne w różnych dziedzinach nauki i technologii.
W matematyce logarytmy odgrywają istotną rolę w analizie funkcji, rozwiązywaniu równań oraz w teorii liczb. Ich zastosowanie wykracza jednak poza samą matematykę. Logarytmy znajdują zastosowanie w naukach przyrodniczych, inżynierii, a także w finansach, gdzie pomagają w obliczaniu wzrostu inwestycji czy analizy danych. Zrozumienie logarytmów jest zatem niezbędne, aby móc efektywnie pracować z danymi i modelami matematycznymi.
Co to jest logarytm i jak go zdefiniować?
Logarytm to funkcja matematyczna, która odpowiada na pytanie, jaką potęgę należy podnieść do danej podstawy $$a$$, aby uzyskać liczbę $$b$$. Formalnie, logarytm można zdefiniować jako $$\log_{a}b = x$$, co jest równoważne stwierdzeniu, że $$a^x = b$$. Logarytmy posiadają kilka ważnych właściwości, takich jak: logarytm iloczynu, który jest równy sumie logarytmów składników, oraz logarytm ilorazu, który jest różnicą logarytmów. Te właściwości są niezwykle użyteczne w różnych obliczeniach matematycznych.
Dlaczego logarytmy są istotne w różnych dziedzinach?
Logarytmy mają szerokie zastosowanie w wielu dziedzinach, w tym w naukach ścisłych, inżynierii i finansach. W fizyce, na przykład, logarytmy są wykorzystywane do analizy zjawisk eksponencjalnych, takich jak rozpad radioaktywny. W inżynierii, logarytmy pomagają w obliczeniach związanych z sygnałami i systemami. W finansach, logarytmy są niezbędne do obliczania wartości przyszłej inwestycji oraz w analizie ryzyka. Zrozumienie logarytmów umożliwia specjalistom w tych dziedzinach lepsze modelowanie i przewidywanie zachowań systemów, co jest kluczowe dla podejmowania trafnych decyzji.
Proste metody obliczania logarytmów dla różnych podstaw
Obliczanie logarytmów może być proste, gdy korzystamy z odpowiednich narzędzi. Kalkulatory naukowe są niezwykle pomocne, ponieważ pozwalają na szybkie i dokładne obliczenia logarytmów dla różnych podstaw. Wystarczy wprowadzić wartość, dla której chcemy obliczyć logarytm, a następnie wybrać odpowiednią funkcję logarytmiczną. Większość kalkulatorów oferuje opcje dla logarytmu naturalnego oraz logarytmu dziesiętnego, co sprawia, że proces staje się intuicyjny.
Oprócz korzystania z kalkulatorów, istnieją również ręczne metody obliczania logarytmów, które można zastosować, szczególnie dla podstawy 10 i e. Aby obliczyć logarytm ręcznie, należy skorzystać z definicji logarytmu, co oznacza przekształcenie równania $$a^x = b$$. Można także wykorzystać znane wartości logarytmów dla podstawy 10 oraz e, aby znaleźć inne wartości, stosując odpowiednie wzory. Ręczne obliczenia wymagają jednak większej precyzji i zrozumienia właściwości logarytmów.Jak obliczać logarytmy przy użyciu kalkulatora?
Aby obliczyć logarytmy przy użyciu kalkulatora, należy postępować zgodnie z kilkoma prostymi krokami. Po pierwsze, wprowadź wartość, dla której chcesz znaleźć logarytm. Następnie wybierz odpowiednią funkcję logarytmiczną, na przykład logarytm naturalny (ln) lub logarytm dziesiętny (log). Po naciśnięciu przycisku oblicz, kalkulator wyświetli wynik. Pamiętaj, aby upewnić się, że używasz właściwej podstawy, ponieważ wyniki mogą się różnić w zależności od wybranej funkcji.
Ręczne metody obliczania logarytmów dla podstawy 10 i e
Ręczne obliczanie logarytmów dla podstawy 10 i e można zrealizować poprzez znajomość ich wartości. Na przykład, logarytm dziesiętny z 100 wynosi 2, ponieważ $$10^2 = 100$$. Podobnie, logarytm naturalny z e wynosi 1, ponieważ $$e^1 = e$$. Aby znaleźć inne wartości, można stosować właściwości logarytmów, takie jak logarytm iloczynu czy ilorazu, co pozwala na przekształcanie bardziej skomplikowanych równań do prostszych form. Ręczne metody wymagają praktyki, ale są bardzo efektywne w zrozumieniu podstaw logarytmów.
Czytaj więcej: Tożsamość w matematyce: Zrozumienie równości i jej zastosowań
Praktyczne przykłady obliczeń logarytmicznych w różnych sytuacjach
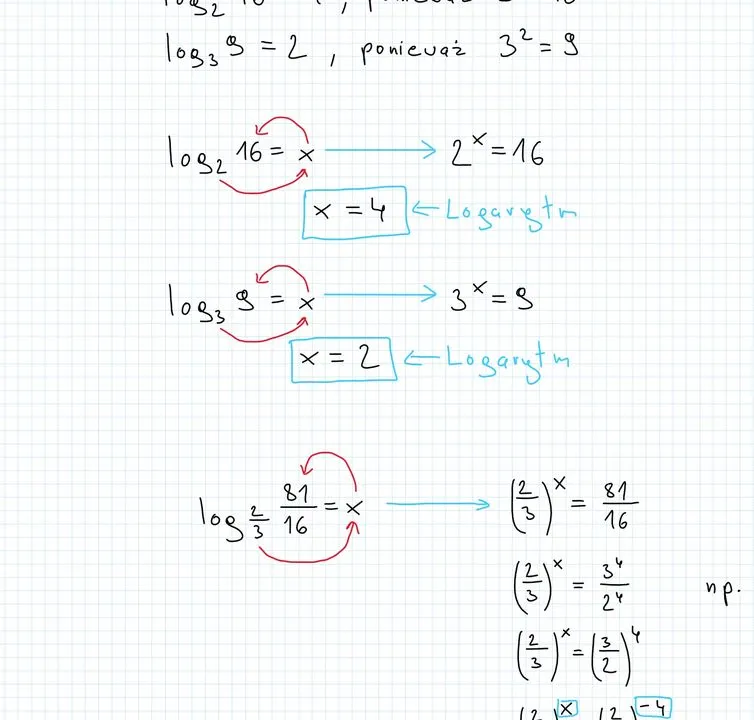
Obliczenia logarytmiczne są niezwykle praktyczne i występują w wielu codziennych sytuacjach. Na przykład, aby obliczyć $$\log_{2}8$$, możemy zauważyć, że $$2^3 = 8$$, więc $$\log_{2}8 = 3$$. Inny przykład to $$\log_{10}1000$$, gdzie $$10^3 = 1000$$, co daje wynik $$\log_{10}1000 = 3$$. Również $$\log_{3}27$$ można obliczyć, ponieważ $$3^3 = 27$$, co prowadzi nas do wyniku $$\log_{3}27 = 3$$. Te przykłady pokazują, jak łatwo można znaleźć wartości logarytmów dla różnych podstaw.
Logarytmy mają wiele zastosowań w rzeczywistych scenariuszach. Na przykład, w finansach logarytmy są używane do obliczania wzrostu inwestycji w czasie. Jeśli inwestycja wzrasta o 10% rocznie, można użyć logarytmu do obliczenia, jak długo zajmie podwojenie tej inwestycji. W naukach przyrodniczych logarytmy pomagają w analizie danych, takich jak stężenie substancji chemicznych w roztworach. Poniżej znajduje się tabela, która porównuje wyniki obliczeń logarytmicznych dla różnych wartości i podstaw.
| Podstawa | Wartość | Wynik logarytmu |
| 2 | 8 | 3 |
| 10 | 1000 | 3 |
| 3 | 27 | 3 |
| 2 | 16 | 4 |
| 10 | 100 | 2 |
Zastosowanie logarytmów w problemach rzeczywistych
Logarytmy znajdują szerokie zastosowanie w wielu dziedzinach życia codziennego oraz w nauce. W finansach, logarytmy są używane do obliczania wzrostu inwestycji oraz analizy oprocentowania. Na przykład, gdy inwestycja wzrasta w sposób wykładniczy, logarytmy pozwalają na określenie czasu potrzebnego do podwojenia wartości inwestycji. W naukach przyrodniczych, logarytmy są niezbędne w analizie danych dotyczących stężenia substancji chemicznych w roztworach, gdzie często wykorzystuje się skale logarytmiczne, takie jak skala pH.
W technologii logarytmy są wykorzystywane w algorytmach kompresji danych oraz w teorii informacji, gdzie pomagają w ocenie efektywności przesyłania informacji. W statystyce, logarytmy są używane do transformacji danych, co umożliwia lepsze modelowanie i analizę rozkładów. W każdym z tych przypadków, zrozumienie i umiejętność obliczania logarytmów są kluczowe dla skutecznego rozwiązywania problemów i podejmowania decyzji.
Najczęstsze błędy w obliczaniu logarytmów i jak ich unikać
Podczas obliczania logarytmów, wiele osób popełnia typowe błędy, które mogą prowadzić do mylnych wyników. Jednym z najczęstszych błędów jest nieprawidłowe określenie podstawy logarytmu. Użytkownicy często mylą podstawy, co skutkuje błędnymi obliczeniami. Innym powszechnym błędem jest ignorowanie zasady, że logarytm z 1 dla dowolnej podstawy (gdzie $$a > 0$$ i $$a \neq 1$$) zawsze wynosi 0. Ważne jest również, aby pamiętać, że logarytm z liczby równej podstawie wynosi 1, co również jest często pomijane.
Aby właściwie interpretować wyniki obliczeń logarytmicznych, warto zwrócić uwagę na kontekst, w jakim są one używane. Na przykład, w finansach, logarytmy mogą być używane do określenia czasu wzrostu inwestycji, ale ich interpretacja wymaga zrozumienia podstawowych zasad dotyczących oprocentowania. W naukach przyrodniczych, wyniki logarytmiczne mogą wskazywać na stężenie substancji, ale ich znaczenie zależy od kontekstu eksperymentu. Dlatego kluczowe jest, aby nie tylko obliczać logarytmy, ale także umieć je odpowiednio interpretować w danym kontekście.
Typowe nieporozumienia dotyczące logarytmów i ich obliczeń
Istnieje wiele typowych nieporozumień związanych z logarytmami, które mogą prowadzić do błędnych obliczeń. Jednym z nich jest przekonanie, że logarytm zawsze musi być większy od zera. W rzeczywistości, logarytmy mogą przyjmować wartości ujemne, szczególnie gdy obliczamy logarytmy dla ułamków. Innym powszechnym nieporozumieniem jest mylenie logarytmu naturalnego z logarytmem dziesiętnym; każdy z nich ma inną podstawę i zastosowanie. Zrozumienie tych różnic jest kluczowe dla poprawnego stosowania logarytmów w praktyce.
Jak poprawnie interpretować wyniki obliczeń logarytmicznych?
Aby właściwie interpretować wyniki obliczeń logarytmicznych, kluczowe jest zrozumienie kontekstu, w jakim są one używane. Na przykład, wynik logarytmu $$\log_{10}1000 = 3$$ oznacza, że liczba 1000 jest równoważna $$10^3$$, co wskazuje na potęgę, do której należy podnieść podstawę 10, aby uzyskać tę wartość. W finansach, logarytmy mogą być używane do obliczenia czasu potrzebnego na podwojenie inwestycji; w takim przypadku wynik logarytmu powinien być interpretowany jako liczba lat potrzebnych do osiągnięcia określonego wzrostu. Ważne jest również, aby pamiętać, że logarytmy mogą przyjmować wartości ujemne, co jest szczególnie istotne przy analizie ułamków.
Wizualizacje i diagramy wspierające naukę logarytmów
Wizualizacje i diagramy są niezwykle pomocne w nauce logarytmów, ponieważ umożliwiają zrozumienie ich właściwości w bardziej przystępny sposób. Różne typy wykresów, takie jak wykresy funkcji logarytmicznych, pomagają zobrazować, jak logarytmy zmieniają się w zależności od wartości argumentu. Dzięki wizualizacjom można łatwiej dostrzegać zależności między wartościami oraz zrozumieć, dlaczego logarytmy mają określone właściwości, takie jak monotoniczność czy asymptoty.
Przykłady użytecznych diagramów obejmują wykresy funkcji logarytmicznych dla różnych podstaw, takich jak $$\log_{10}x$$ czy $$\ln x$$. Wykresy te pokazują, jak wartości logarytmiczne zmieniają się w zależności od argumentu, co ułatwia zrozumienie, jak logarytmy działają w praktyce. Inne wizualizacje mogą obejmować skale logarytmiczne, które są często używane w naukach przyrodniczych, na przykład w pomiarach pH, gdzie wartości są przedstawiane w skali logarytmicznej.
Jak wykorzystać wykresy do zrozumienia logarytmów?
Wykresy są potężnym narzędziem do zrozumienia logarytmów, ponieważ pozwalają na wizualizację ich właściwości. Na przykład, wykres funkcji $$y = \log_{10}x$$ pokazuje, jak wartość logarytmu rośnie wraz ze wzrostem argumentu. Wartości logarytmiczne mają charakter rosnący, co oznacza, że im większa wartość $$x$$, tym większy wynik $$\log_{10}x$$. Dzięki wykresom można również dostrzegać asymptoty, które wskazują, że logarytm nigdy nie osiągnie wartości ujemnych dla dodatnich argumentów. Użycie wykresów ułatwia również zrozumienie, jak logarytmy mogą być stosowane w różnych kontekstach, takich jak analiza danych czy modelowanie zjawisk naturalnych.Przykłady wizualizacji obliczeń logarytmicznych w praktyce
W praktyce, wizualizacje mogą przybierać różne formy, aby pomóc w zrozumieniu logarytmów. Na przykład, wykresy porównawcze mogą pokazywać różnice między funkcjami logarytmicznymi o różnych podstawach, co ułatwia zrozumienie, jak zmieniają się wyniki w zależności od wybranej podstawy. Innym przykładem są diagramy przedstawiające skale logarytmiczne, które ilustrują, jak wartości zmieniają się w kontekście pomiarów, takich jak stężenie substancji chemicznych. Użycie takich wizualizacji pozwala na lepsze zrozumienie złożonych koncepcji logarytmicznych i ich zastosowania w praktyce.
Jak logarytmy wspierają analizę danych w erze big data
W dobie big data i zaawansowanej analizy danych, logarytmy odgrywają kluczową rolę w przetwarzaniu i interpretacji ogromnych zbiorów informacji. Dzięki logarytmicznym skalom, analitycy mogą efektywniej zarządzać danymi, które rozciągają się na wiele rzędów wielkości. Na przykład, w analizie danych dotyczących użytkowników w mediach społecznościowych, logarytmy mogą pomóc w identyfikacji wzorców zachowań oraz w przewidywaniu przyszłych trendów. Umożliwiają one przekształcenie złożonych danych w bardziej zrozumiałe formy, co jest niezbędne w podejmowaniu decyzji opartych na danych.
Co więcej, w kontekście uczenia maszynowego, logarytmy są wykorzystywane w algorytmach optymalizacji, gdzie pomagają w minimalizacji błędów predykcji. Wykorzystując logarytmy w funkcjach strat, można lepiej dostosować modele do złożonych danych, co prowadzi do bardziej precyzyjnych prognoz. W miarę jak technologia rozwija się, a zbiory danych stają się coraz większe, umiejętność stosowania logarytmów w analizie danych będzie kluczowa dla specjalistów w różnych dziedzinach, od finansów po medycynę.

