W artykule omówimy nie tylko definicje i podstawowe pojęcia związane z całkami, ale także ich zastosowania w różnych dziedzinach, takich jak geometria i fizyka. Zbadamy również metody obliczania całek, w tym techniki, które ułatwiają te procesy. Dzięki temu czytelnicy zdobędą solidną wiedzę na temat całek oraz ich praktycznego wykorzystania w matematyce.
Najważniejsze informacje:
- Całka nieoznaczona to zbiór wszystkich funkcji pierwotnych danej funkcji, z wynikiem zawierającym stałą całkowania.
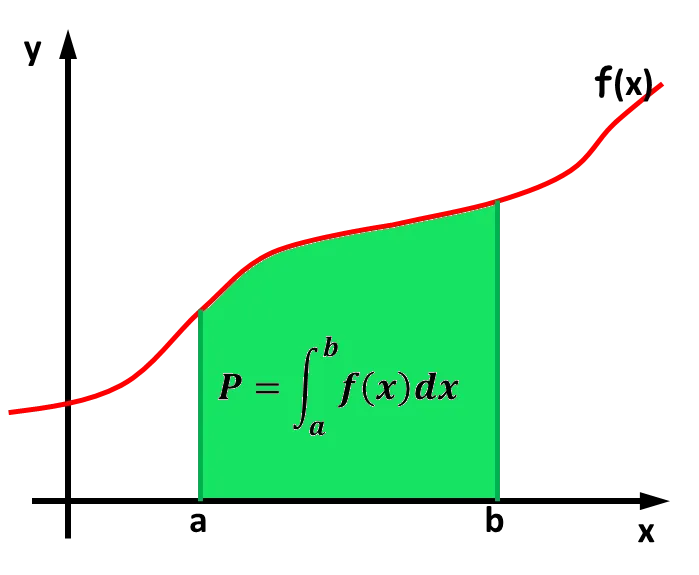
- Całka oznaczona pozwala na obliczenie pola powierzchni pod wykresem funkcji w określonym przedziale.
- Całki mają szerokie zastosowania w różnych dziedzinach, takich jak geometria i fizyka, gdzie służą do obliczania pól, objętości oraz pracy.
- Metody obliczania całek obejmują całkowanie przez podstawienie oraz całkowanie przez części, które są kluczowe dla uproszczenia obliczeń.
- Wyróżniamy różne rodzaje całek, takie jak całka Riemanna i Lebesgue’a, które różnią się podejściem do obliczeń.
Całka w matematyce: Definicje i podstawowe pojęcia
Całka w matematyce to jedno z podstawowych pojęć rachunku różniczkowego i całkowego, które pozwala na wyznaczanie funkcji pierwotnej. Całkowanie jest procesem odwrotnym do różniczkowania, co oznacza, że umożliwia obliczenie wartości całkowitej z wielu małych elementów. Istnieją dwa główne typy całek: całka nieoznaczona oraz całka oznaczona, które różnią się zarówno definicją, jak i zastosowaniem.
Całka nieoznaczona, oznaczana symbolem $$\int f(x) \, dx$$, jest zbiorem wszystkich funkcji pierwotnych funkcji $$f(x)$$. Wynik tej całki zawiera stałą całkowania $$C$$, ponieważ funkcje pierwotne różnią się między sobą o stałą wartość. Z kolei całka oznaczona, zapisywana jako $$\int_a^b f(x) \, dx$$, jest zdefiniowana na konkretnym przedziale $$[a, b]$$ i pozwala na obliczenie pola powierzchni między wykresem funkcji $$f(x)$$ a osią odciętych w tym przedziale. Wartości całki oznaczonej są szczególnie istotne w kontekście obliczeń związanych z geometrią i fizyką.
Całka nieoznaczona: Co to jest i jak ją zrozumieć?
Całka nieoznaczona jest fundamentalnym pojęciem w matematyce, które pozwala na znajdowanie funkcji pierwotnych. Oznacza to, że dla danej funkcji $$f(x)$$, całka nieoznaczona $$\int f(x) \, dx$$ daje nam zbiór wszystkich funkcji, których pochodna jest równa $$f(x)$$. W praktyce, obliczanie całek nieoznaczonych jest kluczowe w wielu dziedzinach matematyki, ponieważ pozwala na analizę zachowania funkcji w różnych kontekstach.
Na przykład, całka nieoznaczona z funkcji $$f(x) = 2x$$ wynosi $$\int 2x \, dx = x^2 + C$$, gdzie $$C$$ to stała całkowania. Oznacza to, że każda funkcja w postaci $$x^2 + C$$ jest funkcją pierwotną dla $$f(x) = 2x$$. Dzięki całkom nieoznaczonym możemy więc zrozumieć, jak zmieniają się wartości funkcji w zależności od jej argumentu.
Całka oznaczona: Definicja i jej znaczenie w matematyce
Całka oznaczona, oznaczana symbolem $$\int_a^b f(x) \, dx$$, jest kluczowym pojęciem w rachunku całkowym. Definiuje się ją na podstawie konkretnego przedziału $$[a, b]$$, w którym oblicza się pole powierzchni znajdujące się między wykresem funkcji $$f(x)$$ a osią odciętych. Wartości tej całki mogą być dodatnie lub ujemne, w zależności od tego, czy funkcja znajduje się powyżej, czy poniżej osi x. Całka oznaczona jest istotna w wielu dziedzinach matematyki, ponieważ pozwala na analizę obszarów i objętości, a także na rozwiązywanie równań różniczkowych.Na przykład, całka oznaczona z funkcji $$f(x) = 2x$$ na przedziale $$[1, 3]$$ oblicza się jako $$\int_1^3 2x \, dx$$. Po obliczeniach otrzymujemy $$[x^2]_1^3 = 3^2 - 1^2 = 9 - 1 = 8$$, co oznacza, że pole powierzchni pod wykresem funkcji $$f(x)$$ od $$x=1$$ do $$x=3$$ wynosi 8 jednostek kwadratowych. Taki sposób obliczania jest niezwykle przydatny w praktycznych zastosowaniach matematyki, takich jak obliczanie pól powierzchni w geometrii.
Zastosowania całek w różnych dziedzinach matematyki
Całki mają szerokie zastosowanie w różnych dziedzinach matematyki, w tym w geometrii i fizyce. W geometrii całki są stosowane do obliczania pól powierzchni oraz objętości różnych kształtów. Przykładowo, całki pozwalają na dokładne wyznaczenie pola powierzchni pod krzywą, co jest niezbędne w analizie kształtów nieregularnych. Dzięki całkom można także obliczać długości łuków oraz objętości brył, co jest kluczowe w projektowaniu i inżynierii.
W fizyce całki odgrywają równie ważną rolę. Używane są do obliczania pracy wykonanej przez siły, a także do wyznaczania momentów siły i środków masy. Na przykład, całka może być użyta do obliczenia pracy wykonaną przez siłę stałą działającą na obiekt na określonym odcinku. Przykładowo, praca wykonana przez siłę $$F$$ na przesunięciu $$d$$ można obliczyć jako $$W = \int F \, dx$$, co pozwala na precyzyjne określenie energii wymaganą do przemieszczenia obiektu w danym kierunku.
Całki w geometrii: Obliczanie pól i objętości
Całki odgrywają kluczową rolę w geometrii, umożliwiając obliczanie pól powierzchni oraz objętości różnych kształtów. Dzięki całkom można precyzyjnie określić, jaką przestrzeń zajmuje dany obiekt, co jest niezbędne w wielu dziedzinach, takich jak inżynieria, architektura czy grafika komputerowa. Na przykład, całki pozwalają na obliczenie pola powierzchni pod krzywą, co jest szczególnie przydatne w analizie kształtów nieregularnych. Wykorzystując całki, można także określić objętości brył, co jest istotne w procesie projektowania i modelowania.- Kwadrat: Pole = $$\int_0^a a \, dx = a^2$$
- Prostokąt: Pole = $$\int_0^a b \, dx = a \cdot b$$
- Trójkąt: Pole = $$\int_0^h \frac{b}{h} x \, dx = \frac{1}{2} b \cdot h$$
- Koło: Pole = $$\int_0^{2\pi} \int_0^r r \, dr \, d\theta = \pi r^2$$
- Walec: Objętość = $$\int_0^{2\pi} \int_0^h \int_0^r r \, dr \, dz \, d\theta = \pi r^2 h$$
Metody obliczania całek: Praktyczne podejścia i techniki
W obliczeniach całkowych istnieje wiele metod, które umożliwiają efektywne obliczanie całek. Jedną z popularnych technik jest całkowanie przez podstawienie, które polega na wprowadzeniu zmiennej pomocniczej, aby uprościć wyrażenie całki. Dzięki tej metodzie można przekształcić skomplikowaną całkę w prostszą formę, co znacznie ułatwia obliczenia. Drugą istotną metodą jest całkowanie przez części, które opiera się na regule iloczynu i pozwala na rozdzielenie całki na dwa łatwiejsze do obliczenia składniki. Obie te metody są niezwykle przydatne w różnych kontekstach matematycznych i inżynieryjnych.
Całkowanie przez podstawienie jest szczególnie użyteczne, gdy mamy do czynienia z funkcjami złożonymi. W tej metodzie zmieniamy zmienną na inną, co pozwala na uproszczenie całki. Na przykład, przy obliczaniu $$\int x \cdot \sqrt{x^2 + 1} \, dx$$, możemy zastosować podstawienie $$u = x^2 + 1$$, co prowadzi do prostszej całki. Z kolei całkowanie przez części wykorzystuje wzór $$\int u \, dv = uv - \int v \, du$$, co pozwala na przekształcenie całki w bardziej przystępną formę. Przykładem może być całka $$\int x e^x \, dx$$, którą można obliczyć, stosując tę metodę, co znacznie ułatwia rozwiązanie.
Całkowanie przez podstawienie: Jak uprościć obliczenia?
Całkowanie przez podstawienie to technika, która polega na wprowadzeniu nowej zmiennej, aby uprościć wyrażenie całki. Jest to szczególnie przydatne, gdy całka zawiera funkcje złożone lub wyrażenia, które są trudne do bezpośredniego obliczenia. W praktyce, wybieramy zmienną, która upraszcza całkę, a następnie przekształcamy całkę w nowej zmiennej. Na przykład, przy obliczaniu $$\int 2x \cdot \sqrt{x^2 + 1} \, dx$$, możemy zastosować podstawienie $$u = x^2 + 1$$, co prowadzi do uproszczenia całki do $$\int \sqrt{u} \, du$$, co jest znacznie łatwiejsze do obliczenia.
Całkowanie przez części: Kiedy i jak stosować tę metodę?
Całkowanie przez części to technika, która opiera się na regule iloczynu i jest używana do obliczania całek, które są trudne do rozwiązania w inny sposób. Metoda ta polega na przekształceniu całki w postaci $$\int u \, dv = uv - \int v \, du$$, gdzie $$u$$ i $$dv$$ są odpowiednio funkcjami, które wybieramy w celu uproszczenia całki. Jest to szczególnie przydatne, gdy mamy do czynienia z iloczynem funkcji, takich jak $$x \cdot e^x$$, gdzie jedna z funkcji jest łatwa do zróżnicowania, a druga do całkowania. Całkowanie przez części pozwala na rozdzielenie skomplikowanej całki na prostsze elementy, co ułatwia obliczenia.
Na przykład, aby obliczyć całkę $$\int x e^x \, dx$$, wybieramy $$u = x$$ (co daje $$du = dx$$) oraz $$dv = e^x \, dx$$ (co prowadzi do $$v = e^x$$). Stosując wzór całkowania przez części, otrzymujemy $$\int x e^x \, dx = x e^x - \int e^x \, dx$$. Po obliczeniu drugiej całki, uzyskujemy końcowy wynik $$x e^x - e^x + C$$, gdzie $$C$$ to stała całkowania. Ta metoda jest niezwykle użyteczna w wielu zastosowaniach matematycznych, szczególnie w analizie funkcji złożonych.
Nowoczesne zastosowania całek w analizie danych i AI
W dzisiejszych czasach całki znajdują zastosowanie nie tylko w klasycznej matematyce, ale również w nowoczesnych technologiach, takich jak analiza danych i sztuczna inteligencja. W kontekście analizy danych, całki są wykorzystywane do obliczania wartości oczekiwanych oraz do modelowania rozkładów prawdopodobieństwa. Dzięki temu możliwe jest lepsze zrozumienie danych oraz przewidywanie przyszłych trendów, co jest kluczowe w wielu branżach, od finansów po marketing.
W obszarze sztucznej inteligencji, całki odgrywają istotną rolę w procesach optymalizacji, takich jak uczenie maszynowe. Na przykład, podczas trenowania modeli, takich jak sieci neuronowe, wykorzystuje się całki do obliczania funkcji kosztu, co pozwala na minimalizację błędów i poprawę efektywności algorytmów. W miarę jak technologia rozwija się, możemy spodziewać się, że metody całkowe będą coraz częściej integrowane z nowoczesnymi rozwiązaniami, co otworzy nowe możliwości w analizie i przetwarzaniu danych.

