W matematyce zmienna zależna odgrywa kluczową rolę w zrozumieniu funkcji i ich zachowania. Jest to wartość, która zmienia się w odpowiedzi na zmiany innej zmiennej, zwanej zmienną niezależną. Zmienna zależna, zazwyczaj oznaczana jako "y", przyjmuje różne wartości w zależności od wartości zmiennej niezależnej, oznaczanej jako "x". Przykładowo, w równaniu $$y = 2x + 3$$, wartość $$y$$ zmienia się w zależności od wartości $$x$$. Dzięki temu możemy modelować różne zjawiska oraz analizować dane w różnych dziedzinach, takich jak ekonomia, fizyka czy biologia.
Wizualizacja zmiennych za pomocą wykresów ułatwia zrozumienie ich relacji. Zmienna zależna jest zazwyczaj umieszczana na osi y, a zmienna niezależna na osi x. W artykule przyjrzymy się bliżej definicji zmiennej zależnej, jej zastosowaniom w różnych funkcjach oraz sposobom wizualizacji, które pomagają w interpretacji danych.
Kluczowe informacje:
- Zmienna zależna zmienia się w odpowiedzi na zmiany zmiennej niezależnej.
- Wartość zmiennej zależnej jest często oznaczana jako "y", a zmiennej niezależnej jako "x".
- Przykłady funkcji z zmiennymi zależnymi obejmują funkcje liniowe, kwadratowe i wykładnicze.
- Wizualizacja zmiennych na wykresach pomaga zrozumieć ich relacje.
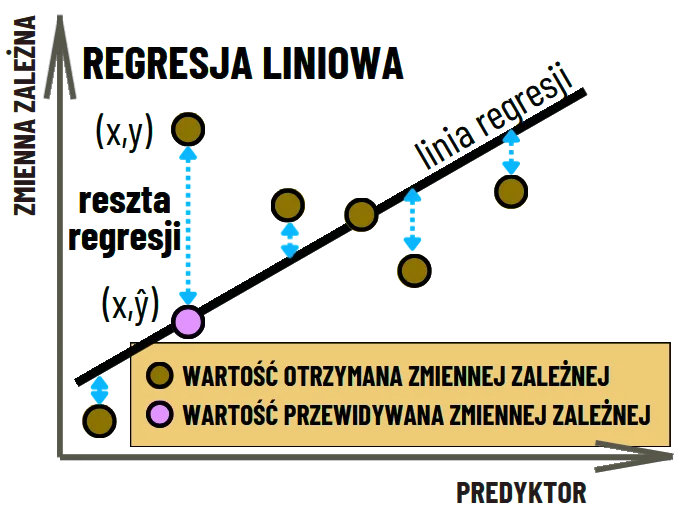
- W kontekście analizy regresji, zmienna zależna jest również nazywana zmienną objaśnianą.
Zdefiniowanie zmiennej zależnej i jej rola w matematyce
Zmiana wartości zmiennej zależnej jest kluczowym aspektem w matematyce, który pozwala na zrozumienie, jak różne czynniki wpływają na siebie. Zmienna zależna to wartość, która zmienia się w odpowiedzi na zmiany innej zmiennej, zwanej zmienną niezależną. Zazwyczaj oznaczana jest jako "y" i przyjmuje różne wartości w zależności od wartości zmiennej niezależnej, oznaczanej jako "x". Zrozumienie tej relacji jest niezbędne do analizy funkcji matematycznych oraz modelowania zjawisk w różnych dziedzinach, takich jak ekonomia czy fizyka.Rola zmiennej zależnej w równaniach matematycznych jest nie do przecenienia. Pozwala ona na określenie, jak jedna zmienna wpływa na drugą, co jest fundamentem dla wielu teorii i zastosowań w praktyce. Właściwe zrozumienie tego konceptu jest kluczowe dla każdego, kto pragnie zgłębić tajniki matematyki i jej zastosowań w rzeczywistości.
Zmienne zależne i niezależne: podstawowe różnice i definicje
W matematyce, zmienne zależne i zmienne niezależne to dwa podstawowe pojęcia, które są ze sobą ściśle powiązane. Zmienna niezależna to ta, którą można kontrolować lub zmieniać, podczas gdy zmienna zależna to ta, która reaguje na zmiany w zmiennej niezależnej. Na przykład, w równaniu funkcji liniowej, zmienna niezależna "x" może przyjmować różne wartości, co wpływa na wartość zmiennej zależnej "y".
Podstawowa różnica między tymi zmiennymi polega na tym, że zmienna niezależna jest przyczyną, a zmienna zależna skutkiem. W praktyce oznacza to, że zmiany w zmiennej niezależnej prowadzą do zmian w zmiennej zależnej. Zrozumienie tej relacji jest kluczowe dla analizy danych i modelowania matematycznego.
Jak zmienna zależna wpływa na funkcje matematyczne?
Zmienna zależna odgrywa kluczową rolę w określaniu zachowania funkcji matematycznych. Jej wartość zmienia się w odpowiedzi na zmiany wartości zmiennej niezależnej, co pozwala na analizę i przewidywanie wyników. W praktyce oznacza to, że dla każdej wartości zmiennej niezależnej, zmienna zależna przyjmuje określoną wartość, co jest fundamentalne dla zrozumienia funkcji. Dzięki tej interakcji, możemy modelować różne zjawiska i zrozumieć, jak różne czynniki wpływają na siebie w matematyce oraz w rzeczywistych zastosowaniach.
Przykłady zastosowania zmiennej zależnej w różnych funkcjach
W kontekście zmiennej zależnej w matematyce, funkcje liniowe są jednym z najprostszych przykładów, które ilustrują jej zastosowanie. W funkcji liniowej, takiej jak $$y = mx + b$$, zmienna zależna "y" zmienia się liniowo w odpowiedzi na zmiany w zmiennej niezależnej "x". Taki model jest powszechnie używany w ekonomii do analizy relacji między różnymi zmiennymi, na przykład w badaniach dotyczących popytu i podaży.
Inne przykłady obejmują funkcje kwadratowe i wykładnicze, gdzie zmienna zależna również odgrywa istotną rolę. W funkcji kwadratowej $$y = ax^2 + bx + c$$, zmienna zależna "y" zmienia się w sposób nieliniowy, co pozwala na modelowanie bardziej skomplikowanych zjawisk, takich jak ruch ciał w fizyce. Z kolei w funkcji wykładniczej $$y = a \cdot e^{bx}$$, zmienna zależna rośnie lub maleje w sposób wykładniczy, co znajduje zastosowanie w wielu dziedzinach, od biologii po finanse.
Analiza funkcji liniowej: zmienna zależna w praktyce
W kontekście zmiennej zależnej w matematyce, funkcje liniowe stanowią doskonały przykład, w jaki sposób zmienna zależna jest reprezentowana. W funkcji liniowej, takiej jak $$y = mx + b$$, zmienna zależna "y" zmienia się w zależności od wartości zmiennej niezależnej "x". To oznacza, że każda zmiana w "x" prowadzi do proporcjonalnej zmiany w "y", co czyni tę funkcję łatwą do analizy i interpretacji. Funkcje liniowe są często stosowane w różnych dziedzinach, takich jak ekonomia, gdzie można modelować relacje między ceną a popytem.
Przykłady zastosowania funkcji liniowych obejmują wiele codziennych sytuacji, takich jak obliczanie kosztów transportu w zależności od przebytej odległości. W takich przypadkach, zmienna zależna (koszt) jest bezpośrednio związana z zmienną niezależną (odległość). Poniższa tabela ilustruje kilka scenariuszy, które można modelować za pomocą funkcji liniowych.
| Scenariusz | Funkcja liniowa |
|---|---|
| Koszt transportu | $$y = 2x + 5$$ (gdzie $$y$$ to koszt, $$x$$ to odległość w km) |
| Wynagrodzenie za godzinę | $$y = 15x$$ (gdzie $$y$$ to wynagrodzenie, $$x$$ to liczba przepracowanych godzin) |
| Sprzedaż produktu | $$y = 10x + 50$$ (gdzie $$y$$ to całkowita sprzedaż, $$x$$ to liczba sprzedanych jednostek) |
Zmienna zależna w funkcjach kwadratowych i wykładniczych
W funkcjach kwadratowych i wykładniczych, zmienna zależna również odgrywa istotną rolę, ale w inny sposób niż w funkcjach liniowych. W funkcji kwadratowej, takiej jak $$y = ax^2 + bx + c$$, zmienna zależna "y" zmienia się w sposób nieliniowy, co pozwala na modelowanie bardziej złożonych zjawisk, takich jak trajektoria ruchu ciał. Na przykład, w fizyce, ruch pocisku można opisać za pomocą funkcji kwadratowej, gdzie zmienna zależna przedstawia wysokość pocisku w zależności od czasu.
Funkcje wykładnicze, takie jak $$y = a \cdot e^{bx}$$, są również niezwykle ważne, szczególnie w kontekście wzrostu populacji lub rozwoju technologii. W tych przypadkach, zmienna zależna "y" rośnie lub maleje w sposób wykładniczy, co znajduje zastosowanie w analizie wzrostu populacji w biologii lub w badaniach finansowych. Oto kilka przykładów, które ilustrują zastosowanie funkcji kwadratowych i wykładniczych:
- Ruch pocisku: $$y = -4.9t^2 + v_0t + h_0$$ (gdzie $$y$$ to wysokość, $$t$$ to czas, $$v_0$$ to prędkość początkowa, $$h_0$$ to wysokość początkowa).
- Wzrost populacji: $$y = P_0 e^{rt}$$ (gdzie $$y$$ to populacja, $$P_0$$ to początkowa populacja, $$r$$ to wskaźnik wzrostu, $$t$$ to czas).
- Rozwój technologii: $$y = A(1 - e^{-kt})$$ (gdzie $$y$$ to poziom adopcji technologii, $$A$$ to maksymalny poziom adopcji, $$k$$ to stała wzrostu).
Czytaj więcej: Co to jest NWW w matematyce? Zrozumienie i przykłady obliczeń
Wizualizacja zmiennej zależnej: grafy i ich interpretacja
Wizualizacja danych za pomocą grafów jest niezwykle istotna dla zrozumienia relacji między zmiennymi, w tym zmienną zależną i zmienną niezależną. Grafy pozwalają na łatwe dostrzeganie wzorców, trendów i anomalii w danych, co jest kluczowe w analizie matematycznej. Dzięki wykresom, można szybko ocenić, jak zmiana jednej zmiennej wpływa na drugą, co jest fundamentem wielu badań i analiz w naukach ścisłych. W kontekście matematyki, zrozumienie wykresów pozwala na lepsze modelowanie zjawisk oraz podejmowanie świadomych decyzji na podstawie danych.Jak czytać wykresy funkcji z zmiennymi zależnymi i niezależnymi?
Odczytywanie wykresów funkcji, które przedstawiają zmienne zależne i niezależne, wymaga uwagi i zrozumienia podstawowych zasad. Pierwszym krokiem jest zidentyfikowanie osi: zmienna niezależna zazwyczaj znajduje się na osi x, a zmienna zależna na osi y. Następnie, warto zwrócić uwagę na skalę wykresu, aby zrozumieć, jak duże są zmiany w danych. Warto również obserwować kształt wykresu, który może wskazywać na liniowość, krzywoliniowość lub inne relacje między zmiennymi. Analizując wykres, można zauważyć, czy istnieje bezpośrednia, odwrotna lub brak relacji między zmiennymi, co jest kluczowe dla interpretacji wyników.
Przykłady wizualizacji: wpływ zmiennej zależnej na kształt wykresu
Wizualizacja zmiennej zależnej ma kluczowe znaczenie w zrozumieniu, jak jej zmiany wpływają na kształt wykresu. Na przykład, w przypadku funkcji liniowej $$y = 2x + 3$$, zmiana wartości zmiennej zależnej "y" powoduje, że linia wykresu przesuwa się w górę lub w dół w zależności od wartości "x". Jeśli z kolei rozważymy funkcję kwadratową $$y = x^2$$, zmiana wartości "x" prowadzi do parabolicznego kształtu wykresu, gdzie zmienna zależna "y" rośnie znacznie szybciej w miarę zwiększania się "x". W funkcjach wykładniczych, takich jak $$y = 3^x$$, nawet niewielkie zmiany w "x" mogą prowadzić do dramatycznych wzrostów w "y", co tworzy stromy wykres.
Te różnice w kształcie wykresów pokazują, jak zmienna zależna wpływa na interpretację danych. W przypadku funkcji wykładniczej, wykres może wskazywać na szybki rozwój, na przykład w kontekście wzrostu populacji. Z kolei w funkcji kwadratowej, zmiany w zmiennej zależnej mogą być użyteczne w analizie trajektorii obiektów w ruchu. Poniższa tabela ilustruje, jak zmiany w zmiennej zależnej wpływają na różne typy wykresów.
| Typ funkcji | Wzór | Opis wpływu zmiennej zależnej |
|---|---|---|
| Funkcja liniowa | $$y = 2x + 3$$ | Prosta linia, zmiana "y" przesuwa wykres w górę/dół. |
| Funkcja kwadratowa | $$y = x^2$$ | Parabola, zmiana "y" rośnie szybciej dla większych "x". |
| Funkcja wykładnicza | $$y = 3^x$$ | Stromy wzrost, niewielkie zmiany "x" powodują duże zmiany "y". |
Zastosowanie zmiennej zależnej w kontekście rzeczywistym
W kontekście naturalnych nauk, zmienna zależna odgrywa kluczową rolę w badaniach biologicznych i fizycznych. Na przykład, w biologii zmienna zależna może reprezentować populację danego gatunku, która zmienia się w odpowiedzi na różne czynniki środowiskowe, takie jak dostępność pokarmu czy zmiany klimatyczne. W fizyce, zmienna zależna może odnosić się do wysokości obiektu w ruchu, co jest analizowane w kontekście grawitacji i sił działających na obiekt. Takie zrozumienie zmiennych zależnych pozwala naukowcom na modelowanie i przewidywanie zachowań systemów naturalnych.
W ekonomii, zmienne zależne są kluczowe w analizie rynków i podejmowaniu decyzji finansowych. Na przykład, w modelach popytu i podaży, cena danego produktu jest zmienną zależną, która zmienia się w odpowiedzi na zmiany w popycie. Wzrost popytu na produkt prowadzi do wzrostu jego ceny, co można zobrazować na wykresach. Analiza tych zmiennych pozwala przedsiębiorcom i analitykom na lepsze zrozumienie rynku oraz podejmowanie bardziej świadomych decyzji dotyczących inwestycji i strategii sprzedaży.
Praktyczne zastosowanie analizy zmiennych w prognozowaniu
W kontekście zmiennej zależnej, jej analiza może być niezwykle pomocna w prognozowaniu przyszłych trendów w różnych dziedzinach. Na przykład, w marketingu, firmy mogą wykorzystać dane o zmiennej zależnej, takiej jak sprzedaż, aby przewidzieć, jak zmiany w kampaniach reklamowych wpłyną na przyszłe przychody. Użycie modeli regresji, które uwzględniają zmienne zależne i niezależne, pozwala na dokładniejsze prognozowanie i lepsze dostosowanie strategii marketingowych do potrzeb rynku.
Co więcej, w kontekście nauk przyrodniczych, analiza zmiennych zależnych może wspierać badania nad zmianami klimatycznymi. Naukowcy mogą modelować, jak zmiany w temperaturze (zmienna niezależna) wpływają na populacje różnych gatunków (zmienna zależna). Tego rodzaju analizy nie tylko pomagają w zrozumieniu obecnych trendów, ale również w przewidywaniu przyszłych zmian, co jest kluczowe dla ochrony środowiska i zarządzania zasobami naturalnymi. W miarę jak technologia analizy danych staje się coraz bardziej zaawansowana, możliwości prognozowania oparte na zmiennych zależnych będą się tylko zwiększać, co przyniesie korzyści w wielu aspektach życia społecznego i gospodarczego.





