- Podnoszenie obu stron równania do kwadratu pozwala na usunięcie pierwiastka.
- Aby usunąć pierwiastek w mianowniku, można pomnożyć licznik i mianownik przez ten sam pierwiastek.
- W przypadku złożonych równań warto wykorzystać sprzężenie mianownika.
- Najczęstsze błędy obejmują niewłaściwe przekształcenia i brak sprawdzenia wyników.
- Weryfikacja poprawności rozwiązania jest kluczowa, aby upewnić się, że uzyskane wyniki są prawidłowe.
Jak skutecznie usunąć pierwiastek z równania - prosta metoda
Usuwanie pierwiastków z równań to kluczowy krok w procesie rozwiązywania problemów matematycznych. Uproszczenie równań poprzez eliminację pierwiastków przynosi wiele korzyści, takich jak zwiększenie przejrzystości i ułatwienie dalszych obliczeń. Kiedy pierwiastek jest obecny, może on wprowadzać zamieszanie i komplikować proces rozwiązywania. Dlatego warto znać metody, które pozwalają na jego usunięcie, co pozwala na skuteczniejsze przekształcanie równań.
W praktyce, usunięcie pierwiastka z równania nie tylko ułatwia jego rozwiązanie, ale także umożliwia zastosowanie prostszych metod analizy i obliczeń. W codziennym życiu matematyka jest obecna w wielu sytuacjach, od obliczeń finansowych po inżynierię. Zrozumienie, kiedy i jak można uprościć równania, jest nie tylko przydatne w szkole, ale także w codziennych zastosowaniach.
Kiedy warto pozbyć się pierwiastka z równania - korzyści z uproszczenia
Decyzja o usunięciu pierwiastka z równania powinna być podejmowana w kontekście jego wpływu na dalsze obliczenia. Uproszczenie równań pozwala na szybsze i bardziej efektywne rozwiązania. Na przykład, w przypadku równań z wieloma zmiennymi, usunięcie pierwiastków może pomóc w szybkim wyznaczeniu wartości niewiadomych. Dzięki temu można uniknąć błędów, które mogą pojawić się przy bardziej skomplikowanych obliczeniach.Jak podnieść obie strony równania do kwadratu - krok po kroku
Aby usunąć pierwiastek z równania, jednym z najprostszych sposobów jest podniesienie obu stron równania do kwadratu. Na przykład, jeśli mamy równanie $$Z = \sqrt{R^2 + X^2}$$, podnosimy obie strony do kwadratu, co daje $$Z^2 = R^2 + X^2$$. Następnie możemy przekształcić równanie, aby wyznaczyć R, odejmując $$X^2$$ od obu stron, co prowadzi do $$Z^2 - X^2 = R^2$$. Na końcu, pierwiastkując obie strony, otrzymujemy $$R = \sqrt{Z^2 - X^2}$$.
- Podnieś obie strony równania do kwadratu, aby usunąć pierwiastek.
- Przekształć równanie, aby wyizolować zmienną, której szukasz.
- Sprawdź poprawność rozwiązania, pierwiastkując uzyskaną wartość.
Jak usunąć pierwiastek w mianowniku - efektywne techniki
Eliminacja pierwiastków z mianownika ułamków jest kluczowym krokiem w uproszczeniu równań. Jedną z najskuteczniejszych metod jest mnożenie przez sprzężenie. Kiedy mamy do czynienia z ułamkiem, w którym pierwiastek znajduje się w mianowniku, możemy pomnożyć zarówno licznik, jak i mianownik przez ten sam pierwiastek. Na przykład, rozważmy ułamek $$\frac{6}{\sqrt{3}}$$. Mnożąc licznik i mianownik przez $$\sqrt{3}$$, otrzymujemy $$\frac{6\sqrt{3}}{3}$$, co po uproszczeniu daje $$2\sqrt{3}$$. Dzięki temu pozbywamy się pierwiastka z mianownika, co ułatwia dalsze obliczenia.
Inną techniką, którą warto znać, jest rationalizacja mianownika, szczególnie w przypadkach, gdy mamy złożone wyrażenia. Na przykład, w równaniu $$\frac{1}{\sqrt{a} + \sqrt{b}}$$, możemy pomnożyć licznik i mianownik przez sprzężenie mianownika, czyli $$\sqrt{a} - \sqrt{b}$$. To pozwala nam na uproszczenie wyrażenia i usunięcie pierwiastków z mianownika. Po wykonaniu tych operacji, mamy $$\frac{\sqrt{a} - \sqrt{b}}{a - b}$$, co znacznie ułatwia dalsze prace z równaniem.
Jak poradzić sobie z pierwiastkami w bardziej złożonych równaniach
W przypadku bardziej skomplikowanych równań, które zawierają wiele pierwiastków, warto zastosować różne strategie, aby uprościć obliczenia. Jedną z nich jest izolacja pierwiastka w równaniu. Na przykład, w równaniu $$\sqrt{x + 1} + \sqrt{x - 1} = 5$$, możemy najpierw przenieść jeden z pierwiastków na drugą stronę, co daje $$\sqrt{x + 1} = 5 - \sqrt{x - 1}$$. Następnie, podnosimy obie strony do kwadratu, co pozwala na dalsze uproszczenie równania.
Inną przydatną techniką jest przekształcanie równań w celu eliminacji pierwiastków. Na przykład, w równaniu $$\sqrt{2x + 3} = x - 1$$, możemy podnieść obie strony do kwadratu, co prowadzi do $$2x + 3 = (x - 1)^2$$. Następnie przekształcamy równanie, aby znaleźć wartość x, co pozwala na łatwiejsze rozwiązanie problemu.
| Metoda | Opis |
| Mnożenie przez sprzężenie | Usunięcie pierwiastka z mianownika przez mnożenie przez ten sam pierwiastek. |
| Rationalizacja mianownika | Mnożenie przez sprzężenie, aby uprościć złożone ułamki. |
| Izolacja pierwiastka | Przenoszenie pierwiastków na jedną stronę równania dla uproszczenia. |
Czytaj więcej: Znak nieskończoności w matematyce: co musisz wiedzieć o nim?
Najczęstsze błędy przy usuwaniu pierwiastków - jak ich uniknąć
Podczas pracy z równaniami zawierającymi pierwiastki, łatwo popełnić błędy, które mogą prowadzić do błędnych wyników. Najczęstsze błędy obejmują niewłaściwe podnoszenie obu stron do kwadratu, co może wprowadzić dodatkowe rozwiązania, które nie są zgodne z pierwotnym równaniem. Innym powszechnym błędem jest pomijanie sprawdzenia, czy wynik końcowy spełnia oryginalne równanie, co może prowadzić do fałszywych wniosków. Ważne jest, aby być ostrożnym przy przekształcaniu równań i zawsze upewnić się, że zachowujemy równoważność.
Innym częstym problemem jest niepoprawne traktowanie pierwiastków w mianowniku. Wiele osób zapomina, że przed usunięciem pierwiastka z mianownika należy najpierw pomnożyć przez jego sprzężenie. Unikanie tych błędów jest kluczowe dla uzyskania poprawnych wyników. Warto również zwrócić uwagę na to, aby nie pomijać kroków w obliczeniach, ponieważ każdy z nich ma znaczenie dla ostatecznego wyniku.
Jak sprawdzić poprawność rozwiązania po usunięciu pierwiastka - praktyczne wskazówki
Weryfikacja poprawności rozwiązania po usunięciu pierwiastka jest kluczowym krokiem, który pozwala upewnić się, że uzyskane wyniki są prawidłowe. Po zakończeniu obliczeń warto podstawić uzyskane wartości z powrotem do oryginalnego równania. Dzięki temu możemy sprawdzić, czy lewa strona równania jest równa prawej. Na przykład, jeśli rozwiązaliśmy równanie $$\sqrt{x} = 4$$ i otrzymaliśmy $$x = 16$$, powinniśmy sprawdzić, czy $$\sqrt{16} = 4$$, co jest prawdą.
Innym sposobem na weryfikację jest analiza rozwiązań w kontekście problemu. Czasami warto zastanowić się, czy uzyskana wartość ma sens w danym kontekście. Na przykład, w zadaniach dotyczących długości czy powierzchni, nie możemy uzyskać wartości ujemnych. Regularne sprawdzanie poprawności wyników pozwala uniknąć błędów i zwiększa pewność w obliczeniach.
Jak sprawdzić poprawność rozwiązania po usunięciu pierwiastka - praktyczne wskazówki
Weryfikacja poprawności rozwiązania po usunięciu pierwiastka jest niezwykle ważna, aby upewnić się, że uzyskane wyniki są zgodne z pierwotnym równaniem. Po zakończeniu obliczeń warto podstawić uzyskane wartości z powrotem do oryginalnego równania. Na przykład, jeśli rozwiązaliśmy równanie $$\sqrt{x} = 4$$ i otrzymaliśmy $$x = 16$$, powinniśmy sprawdzić, czy $$\sqrt{16} = 4$$, co jest prawdą. Taka metoda pozwala na potwierdzenie, że nasze obliczenia były prawidłowe i że nie popełniliśmy błędów w trakcie rozwiązywania.
Innym sposobem na weryfikację jest analiza uzyskanych rozwiązań w kontekście problemu. Czasami warto zastanowić się, czy uzyskana wartość ma sens w danym kontekście. Na przykład, w zadaniach dotyczących długości czy powierzchni, nie możemy uzyskać wartości ujemnych. Regularne sprawdzanie poprawności wyników pozwala uniknąć błędów i zwiększa pewność w obliczeniach. Pamiętaj, aby nie tylko sprawdzić wyniki, ale także zrozumieć ich znaczenie w kontekście problemu, który rozwiązujesz.
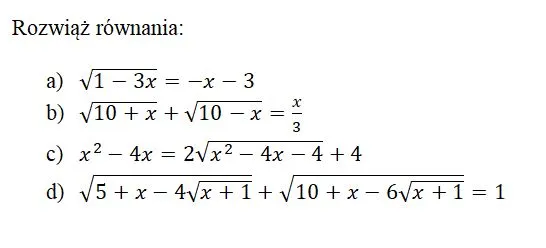
Jak pozbyć się pierwiastka z równania - proste metody i przykłady
Usuwanie pierwiastków z równań jest kluczowym krokiem w matematyce, który ułatwia rozwiązywanie problemów. W tym artykule przedstawimy różne metody, które pozwalają na eliminację pierwiastków w równaniach, co może znacząco uprościć proces obliczeń. Zaczniemy od omówienia korzyści płynących z uproszczenia równań, a następnie przejdziemy do konkretnych technik, takich jak podnoszenie obu stron równania do kwadratu oraz usuwanie pierwiastków z mianownika. Każda metoda będzie ilustrowana konkretnymi przykładami, co pomoże lepiej zrozumieć zastosowanie tych technik w praktyce.
Ważne jest, aby zrozumieć, że usunięcie pierwiastka z równania nie tylko ułatwia dalsze przekształcenia, ale także pozwala na szybsze i bardziej efektywne rozwiązanie problemu. Dzięki przedstawionym metodom, każdy będzie mógł z łatwością radzić sobie z równaniami, które na pierwszy rzut oka mogą wydawać się skomplikowane. Przykłady, które zaprezentujemy, będą praktycznymi ilustracjami zastosowania omawianych technik w rzeczywistych zadaniach matematycznych.
Przykład 1: Uproszczenie równania z pierwiastkiem
Rozważmy równanie $$Z = \sqrt{R^2 + X^2}$$. Aby usunąć pierwiastek, podnosimy obie strony do kwadratu, co daje $$Z^2 = R^2 + X^2$$. Następnie możemy przekształcić równanie, aby wyznaczyć R, odejmując $$X^2$$ od obu stron, co prowadzi do $$R^2 = Z^2 - X^2$$. Na koniec, pierwiastkując obie strony, otrzymujemy $$R = \sqrt{Z^2 - X^2}$$. Dzięki tej metodzie, pierwiastek został skutecznie usunięty, co pozwala na dalsze obliczenia.
Przykład 2: Eliminacja pierwiastka w mianowniku
Weźmy ułamek $$\frac{6}{\sqrt{3}}$$. Aby usunąć pierwiastek z mianownika, mnożymy zarówno licznik, jak i mianownik przez $$\sqrt{3}$$, co daje $$\frac{6\sqrt{3}}{3}$$. Po uproszczeniu otrzymujemy $$2\sqrt{3}$$. Ta technika jest niezwykle przydatna, gdy mamy do czynienia z ułamkami, w których pierwiastek znajduje się w mianowniku, ponieważ pozwala to na uproszczenie wyrażenia do bardziej przystępnej formy.
- Podnieś obie strony równania do kwadratu, aby usunąć pierwiastek.
- Mnożenie przez sprzężenie pozwala na eliminację pierwiastków w mianownikach.
- Sprawdzaj poprawność uzyskanych wyników, podstawiając je z powrotem do oryginalnego równania.
Jak zastosować usuwanie pierwiastków w praktycznych zadaniach życiowych
Usuwanie pierwiastków z równań nie ogranicza się tylko do zadań matematycznych w szkole. W codziennym życiu umiejętność ta może być niezwykle przydatna, szczególnie w dziedzinach takich jak inżynieria, architektura czy finanse. Na przykład, w inżynierii często trzeba obliczać siły działające na konstrukcje, gdzie równania mogą zawierać pierwiastki. Umiejętność ich eliminacji pozwala na szybsze i bardziej efektywne przeprowadzanie analiz strukturalnych, co jest kluczowe dla bezpieczeństwa budynków i innych obiektów.
Dodatkowo, w finansach, gdy obliczamy różne wskaźniki, takie jak rentowność inwestycji, często napotykamy na równania z pierwiastkami. Uproszczenie tych równań umożliwia szybsze podejmowanie decyzji inwestycyjnych. Warto zatem rozwijać umiejętności związane z eliminacją pierwiastków, aby móc je stosować w różnych kontekstach, co z pewnością przyniesie korzyści w wielu aspektach życia zawodowego i osobistego.





