Przykłady, które zostaną przedstawione, pokazują różne metody uproszczenia, takie jak redukcja wyrazów podobnych oraz zastosowanie właściwości działań matematycznych. Oprócz tego, omówimy powszechne błędy, które mogą wystąpić podczas tego procesu, oraz sposoby ich unikania. Dzięki tym informacjom, staniesz się bardziej pewny w pracy z wyrażeniami algebraicznymi.
Kluczowe informacje:
- Obwód kwadratu o boku długości $x+3$ można uprościć do postaci $4x + 12$.
- Uproszczenie wyrażeń algebraicznych polega na łączeniu wyrazów podobnych oraz stosowaniu właściwości działań matematycznych.
- Przykłady uproszczeń obejmują wyrażenia z nawiasami oraz operacje mnożenia i dzielenia.
- Najczęstsze błędy to niewłaściwe stosowanie właściwości matematycznych oraz przeoczenie znaków.
- Weryfikacja wyników po uproszczeniu jest kluczowa dla zapewnienia poprawności obliczeń.
Zrozumienie wyrażeń algebraicznych i ich uproszczenie
Wyrażenia algebraiczne to kombinacje liter (zmiennych), cyfr (stałych) oraz działań matematycznych, takich jak dodawanie, odejmowanie, mnożenie i dzielenie. Przykładem wyrażenia algebraicznego jest $2x + 3$, gdzie $x$ jest zmienną, a $2$ i $3$ to stałe. Wyrażenia te mogą mieć różne formy, w tym wielomiany, które zawierają potęgi zmiennych, jak $x^2 + 4x + 7$. Ważne jest, aby zrozumieć, że wyrażenia algebraiczne są podstawą bardziej złożonych równań i funkcji w matematyce.Uproszczenie wyrażeń algebraicznych jest kluczowe, ponieważ pozwala na łatwiejsze rozwiązywanie równań i przyspiesza proces obliczeń. Kiedy wyrażenia są uproszczone, stają się bardziej czytelne i zrozumiałe, co ułatwia ich analizę i wykorzystanie w praktycznych zastosowaniach. Na przykład, uproszczenie wyrażenia, które opisuje obwód kwadratu, pozwala na szybkie obliczenie jego wartości bez zbędnych komplikacji. Dlatego umiejętność uproszczenia wyrażeń algebraicznych jest niezbędna dla każdego, kto chce efektywnie pracować z matematyką.
Co to są wyrażenia algebraiczne i jak je definiujemy
Wyrażenia algebraiczne składają się z zmiennych, stałych i operatorów, które łączą te elementy w jedną całość. Zmienna to symbol, najczęściej litera, która reprezentuje liczbę, np. $x$ lub $y$. Stała to konkretna liczba, jak $2$ czy $5$. Operatorzy to działania, które wykonujemy na tych elementach, takie jak dodawanie (+), odejmowanie (-), mnożenie (×) i dzielenie (÷). Na przykład, w wyrażeniu $3x + 4$, $3$ jest współczynnikiem, który mnoży zmienną $x$, a $4$ jest stałą. Wyrażenia algebraiczne mogą być proste lub złożone, w zależności od liczby użytych zmiennych i operatorów.
Dlaczego uproszczenie wyrażeń algebraicznych jest ważne
Uproszczenie wyrażeń algebraicznych jest kluczowym krokiem w matematyce, który przynosi wiele korzyści. Po pierwsze, ułatwia obliczenia, co pozwala na szybsze i bardziej efektywne rozwiązywanie równań. Gdy wyrażenia są uproszczone, stają się bardziej przejrzyste, co ułatwia ich zrozumienie i interpretację. Na przykład, uproszczenie obwodu kwadratu do postaci $4x + 12$ pozwala na szybkie oszacowanie jego wartości, zamiast zajmowania się bardziej skomplikowanymi formami.
Po drugie, uproszczenie wyrażeń algebraicznych ma istotne znaczenie w rozwiązywaniu problemów w rzeczywistych sytuacjach. W praktyce, wiele zadań matematycznych wymaga przekształcania złożonych wyrażeń w prostsze formy, co ułatwia ich zastosowanie w różnych dziedzinach, takich jak inżynieria, ekonomia czy nauki przyrodnicze. Dzięki uproszczeniu, można skupić się na kluczowych aspektach problemu, eliminując zbędne komplikacje.
Metody uproszczenia wyrażeń algebraicznych krok po kroku
Uproszczenie wyrażeń algebraicznych można osiągnąć na różne sposoby. Kluczowe metody obejmują redukcję wyrazów podobnych, co polega na łączeniu składników o tych samych zmiennych, oraz zastosowanie właściwości działań matematycznych, takich jak właściwość rozdzielności. Te metody są fundamentalne dla każdego, kto chce zapisać wyrażenia algebraiczne w najprostszej postaci.
W praktyce, stosowanie tych metod wymaga zrozumienia, jak działają poszczególne operacje matematyczne. Na przykład, przy redukcji wyrazów podobnych, należy dokładnie zidentyfikować, które składniki można połączyć. Z kolei właściwości działań matematycznych, takie jak przemienność i łączność, mogą pomóc w reorganizacji wyrażeń w sposób, który ułatwia ich uproszczenie. Warto zatem poznać te techniki, aby skutecznie pracować z wyrażeniami algebraicznymi.
Uproszczenie przez redukcję wyrazów podobnych
Redukcja wyrazów podobnych to kluczowy proces w uproszczeniu wyrażeń algebraicznych. Polega on na łączeniu składników, które mają te same zmienne z identycznymi potęgami. Na przykład, w wyrażeniu $4x^2 + 3x - 2 + 5x^2$, możemy połączyć $4x^2$ i $5x^2$, uzyskując $9x^2$. Ważne jest, aby dokładnie zidentyfikować, które składniki można ze sobą zestawić, co znacząco upraszcza obliczenia.
- $3x + 2x = 5x$ - łączenie podobnych wyrazów z zmienną $x$.
- $7y^2 - 2y^2 = 5y^2$ - łączenie wyrazów z zmienną $y^2$.
- $6 - 4 + 2 = 4$ - łączenie stałych.
Użycie właściwości działań matematycznych w uproszczeniu
W matematyce istnieje kilka właściwości, które ułatwiają uproszczenie wyrażeń algebraicznych. Właściwość przemienności mówi, że kolejność składników nie ma znaczenia, np. $a + b = b + a$. Właściwość łączności pozwala na grupowanie składników, co oznacza, że $(a + b) + c = a + (b + c)$. Właściwość rozdzielności pozwala na rozdzielenie mnożenia od dodawania, co można zobaczyć w równaniu $a(b + c) = ab + ac$. Te właściwości są niezwykle przydatne w procesie uproszczenia, ponieważ umożliwiają reorganizację wyrażeń w sposób, który ułatwia ich obliczenie.
Przykłady uproszczenia różnych typów wyrażeń algebraicznych
Uproszczenie wyrażeń algebraicznych z nawiasami jest kluczowym krokiem w matematyce. Aby uprościć takie wyrażenia, należy najpierw usunąć nawiasy, stosując odpowiednie działania. Na przykład, w przypadku wyrażenia $3(x + 2) + 4$, najpierw mnożymy $3$ przez każdy składnik w nawiasie, co daje $3x + 6$. Następnie dodajemy $4$, co prowadzi do ostatecznego wyniku $3x + 10$. Proces ten pozwala na przekształcenie skomplikowanej formy w prostszą, co ułatwia dalsze obliczenia.
W przypadku wyrażeń z mnożeniem i dzieleniem, uproszczenie również odgrywa istotną rolę. Na przykład, w wyrażeniu $8x^2 \cdot 4x / 16$, najpierw mnożymy $8$ przez $4$, co daje $32x^2$. Następnie dzielimy przez $16$, co pozwala na uproszczenie do $2x^2$. Użycie tych operacji matematycznych nie tylko upraszcza wyrażenia, ale także czyni je bardziej zrozumiałymi i łatwiejszymi do analizy w kontekście rozwiązywania równań.
Uproszczenie wyrażeń z nawiasami i ich zastosowanie
Aby uprościć wyrażenia zawierające nawiasy, należy stosować kilka kroków. Pierwszym jest zidentyfikowanie nawiasów i ich zawartości. Następnie, przy użyciu właściwości rozdzielności, można pomnożyć składniki znajdujące się poza nawiasami przez te wewnątrz. Na przykład, w wyrażeniu $2(x + 3) - 4$, najpierw mnożymy $2$ przez $x$ i $3$, co daje $2x + 6$. Następnie odejmujemy $4$, co prowadzi do ostatecznego wyniku $2x + 2$. Dzięki tym krokom, wyrażenie z nawiasami staje się prostsze i bardziej przejrzyste.
Zastosowanie mnożenia i dzielenia w uproszczeniu
Mnożenie i dzielenie są kluczowymi operacjami w procesie uproszczenia wyrażeń algebraicznych. Aby uprościć wyrażenia, które zawierają te operacje, należy najpierw wykonać mnożenie lub dzielenie, zanim przejdziemy do innych działań. Na przykład, w wyrażeniu $12x \cdot 3 / 6$, najpierw mnożymy $12$ przez $3$, co daje $36x$, a następnie dzielimy przez $6$, co prowadzi do ostatecznego wyniku $6x$. Taki proces pozwala na uproszczenie wyrażenia do bardziej przystępnej formy, co jest szczególnie przydatne w obliczeniach praktycznych.
Warto również pamiętać, że uproszczenie wyrażeń z mnożeniem i dzieleniem może być stosowane w różnych kontekstach, takich jak obliczenia w fizyce czy ekonomii. Na przykład, jeśli mamy wyrażenie opisujące koszt produkcji, które zawiera mnożenie przez liczbę jednostek i dzielenie przez koszty stałe, uproszczenie pozwoli na łatwiejsze zrozumienie, jak zmiana liczby jednostek wpływa na całkowity koszt. Dlatego umiejętność efektywnego stosowania mnożenia i dzielenia w uproszczeniu wyrażeń algebraicznych jest niezbędna w wielu dziedzinach.
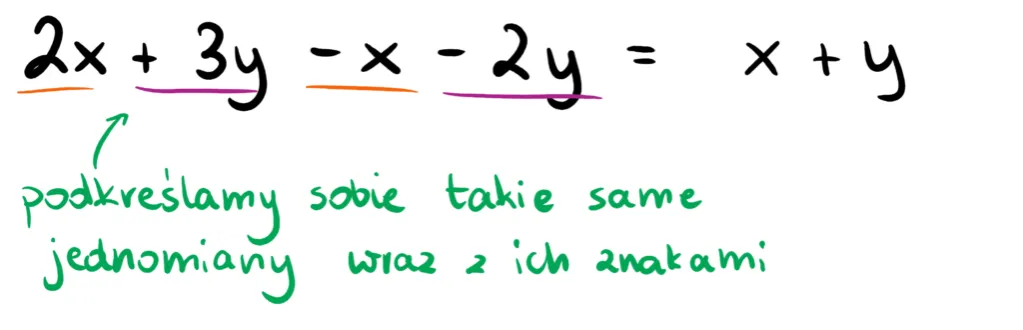
Częste błędy przy upraszczaniu wyrażeń algebraicznych
Podczas upraszczania wyrażeń algebraicznych występuje wiele powszechnych błędów, które mogą prowadzić do niepoprawnych wyników. Jednym z najczęstszych błędów jest niewłaściwe stosowanie nawiasów, co może prowadzić do błędnych wyników. Innym częstym problemem jest zapominanie o znakach, zwłaszcza przy odejmowaniu, co wpływa na końcowy wynik. Dodatkowo, łączenie wyrazów podobnych bez dokładnego sprawdzenia, które składniki można połączyć, również może prowadzić do błędów. Warto zatem być szczególnie uważnym na te pułapki podczas upraszczania.
Aby uniknąć błędów, warto stosować kilka praktycznych wskazówek. Po pierwsze, zawsze sprawdzaj, czy poprawnie używasz nawiasów i czy uwzględniasz wszystkie znaki. Po drugie, po zakończeniu uproszczenia, warto zweryfikować wyniki poprzez podstawienie wartości zmiennych do oryginalnego wyrażenia i porównanie z uproszczonym wynikiem. To pomoże upewnić się, że uproszczenie zostało przeprowadzone prawidłowo. Na koniec, regularne ćwiczenie i rozwiązywanie różnych typów wyrażeń algebraicznych pomoże w rozwijaniu umiejętności i unikania typowych błędów.
Praktyczne zastosowania wyrażeń algebraicznych w codziennym życiu
Wyrażenia algebraiczne znajdują zastosowanie nie tylko w szkołach i na uczelniach, ale również w codziennych sytuacjach, które wymagają obliczeń. Na przykład, w planowaniu budżetu domowego, możemy wykorzystać wyrażenia algebraiczne do obliczenia wydatków w zależności od zmieniających się cen. Jeśli cena jednego produktu wynosi $x$, a planujemy kupić ich $y$, możemy zapisać całkowity koszt jako $C = xy$. Dzięki temu, łatwiej jest zrozumieć, jak zmiana ceny wpływa na nasz budżet.
Dodatkowo, w kontekście analizy danych, wyrażenia algebraiczne są kluczowe w modelowaniu i prognozowaniu. Na przykład, w marketingu można stosować wyrażenia do przewidywania sprzedaży na podstawie różnych czynników, takich jak sezonowość czy kampanie reklamowe. Używając zmiennych, możemy stworzyć model, który pomoże w podejmowaniu lepszych decyzji biznesowych. W ten sposób, umiejętność pracy z wyrażeniami algebraicznymi nie tylko ułatwia rozwiązywanie problemów matematycznych, ale także otwiera drzwi do bardziej zaawansowanych zastosowań w różnych dziedzinach życia.

