Rozwiązywanie równań jest kluczowym elementem matematyki, który pozwala nam znaleźć wartości niewiadomych, spełniających określone warunki. Równanie to wyrażenie, które łączy dwa elementy za pomocą znaku równości, a jego celem jest określenie, jakie liczby pasują do tej struktury. W tym artykule przyjrzymy się skutecznym metodom rozwiązywania równań, zarówno liniowych, jak i kwadratowych, oraz omówimy różne techniki, które mogą ułatwić ten proces.
Rozpoczniemy od podstawowych definicji i zrozumienia, jak działają równania, a następnie przejdziemy do konkretnych przykładów i metod. Dzięki temu każdy, niezależnie od poziomu zaawansowania, będzie mógł skutecznie rozwiązywać różnorodne równania i zdobyć pewność w swoich umiejętnościach matematycznych.
Kluczowe wnioski:
- Równania składają się z wyrażeń połączonych znakiem równości, a ich rozwiązanie polega na odnalezieniu wartości niewiadomych.
- Równania liniowe można rozwiązywać poprzez uproszczenia i przekształcenia, co pozwala na łatwe znalezienie pierwiastków.
- Dla równań kwadratowych stosuje się metodę delty, która umożliwia określenie liczby rozwiązań oraz ich wartości.
- Uproszczenie równań jest kluczowe dla efektywnego rozwiązywania i obejmuje techniki takie jak łączenie podobnych wyrazów czy faktoryzacja.
- Zaawansowane metody, takie jak podstawianie lub eliminacja, są niezbędne w przypadku układów równań i bardziej złożonych problemów.
Jak rozwiązywać równania: podstawowe metody i techniki
Zrozumienie równań: co to jest i jak działają
Równanie to matematyczna struktura, która łączy dwa wyrażenia za pomocą znaku równości. W każdym równaniu występują niewiadome, które są oznaczane literami, oraz stałe, które są liczbami. Rozwiązać równanie oznacza znaleźć wszystkie jego pierwiastki, czyli liczby, które spełniają dane równanie, lub wykazać, że takie liczby nie istnieją. Na przykład, w równaniu $$2x + 3 = 7$$, pierwiastkiem jest liczba $$x = 2$$, ponieważ po podstawieniu tej wartości obie strony równania są równe.Ważne jest, aby zrozumieć, że proces rozwiązywania równań polega na przekształcaniu ich równoważnie. Oznacza to, że wykonujemy te same działania na obu stronach równania, aby uzyskać formę, w której niewiadoma znajduje się po jednej stronie, a liczby po drugiej. Taki sposób działania pozwala na uzyskanie wartości niewiadomej w sposób systematyczny i zrozumiały. Przykładowo, w równaniu $$3x + 1 = 10$$ najpierw odejmujemy 1 od obu stron, co daje $$3x = 9$$, a następnie dzielimy przez 3, uzyskując $$x = 3$$.
Równania liniowe: krok po kroku do rozwiązania
Rozwiązywanie równań liniowych to proces, który można podzielić na kilka prostych kroków. Zaczynamy od przekształcenia równania tak, aby wszystkie niewiadome znalazły się po jednej stronie, a liczby po drugiej. Najczęściej wykonuje się operacje takie jak dodawanie, odejmowanie, mnożenie lub dzielenie, aby uprościć równanie. Kluczowe jest, aby pamiętać o wykonywaniu tych samych działań na obu stronach równania, co pozwala zachować jego równoważność.
Przykład prostego równania liniowego to $$2x + 3 = 11$$. Aby znaleźć wartość niewiadomej $$x$$, najpierw odejmujemy 3 od obu stron, co daje $$2x = 8$$. Następnie dzielimy obie strony przez 2, uzyskując $$x = 4$$. Dzięki temu prostemu procesowi można efektywnie rozwiązywać wiele równań liniowych i znaleźć ich pierwiastki.
- 1. Przenieś wszystkie wyrazy z niewiadomą na jedną stronę równania.
- 2. Uprość równanie, wykonując odpowiednie operacje matematyczne.
- 3. Rozwiąż równanie, dzieląc lub mnożąc przez współczynnik przy niewiadomej.
Równania kwadratowe: zastosowanie metody delty w praktyce
Równania kwadratowe mają postać $$ax^2 + bx + c = 0$$, gdzie $$a$$, $$b$$ i $$c$$ są stałymi, a $$x$$ to niewiadoma. Aby znaleźć pierwiastki takiego równania, stosuje się metodę delty, która polega na obliczeniu wartości delty według wzoru $$\Delta = b^2 - 4ac$$. W zależności od wartości delty, możemy określić liczbę rozwiązań równania. Jeśli $$\Delta > 0$$, równanie ma dwa różne rozwiązania. Gdy $$\Delta = 0$$, istnieje jedno rozwiązanie, a w przypadku $$\Delta < 0$$, równanie nie ma rozwiązań w zbiorze liczb rzeczywistych.Rozważmy przykład równania kwadratowego $$2x^2 - 4x - 6 = 0$$. Najpierw obliczamy deltę: $$\Delta = (-4)^2 - 4 \cdot 2 \cdot (-6) = 16 + 48 = 64$$. Ponieważ $$\Delta > 0$$, równanie ma dwa rozwiązania. Stosując wzory na pierwiastki, mamy: $$x_1 = \frac{-(-4) - \sqrt{64}}{2 \cdot 2} = \frac{4 - 8}{4} = -1$$ oraz $$x_2 = \frac{-(-4) + \sqrt{64}}{2 \cdot 2} = \frac{4 + 8}{4} = 3$$. Zatem pierwiastkami równania są $$x_1 = -1$$ i $$x_2 = 3$$.
| Wartość delty (Δ) | Liczba rozwiązań |
| Δ > 0 | Dwa różne rozwiązania |
| Δ = 0 | Jedno rozwiązanie |
| Δ < 0 | Brak rozwiązań w zbiorze liczb rzeczywistych |
Uproszczenie równań: efektywne techniki i wskazówki
Uproszczenie równań jest kluczowym krokiem w procesie rozwiązywania równań liniowych i kwadratowych. Dzięki efektywnym technikom uproszczenia możemy znacząco ułatwić sobie pracę. Jedną z podstawowych metod jest łączenie podobnych wyrazów, co pozwala na zredukowanie liczby składników w równaniu. Na przykład, w równaniu $$2x + 3x - 5 = 10$$ możemy połączyć $$2x$$ i $$3x$$, co daje $$5x - 5 = 10$$. Inną przydatną techniką jest faktoryzacja, która polega na wyodrębnieniu wspólnego czynnika z wyrazów. Na przykład, w równaniu $$6x^2 + 9x = 0$$ możemy wyciągnąć wspólny czynnik $$3x$$, co prowadzi do $$3x(2x + 3) = 0$$.
Kolejną istotną metodą jest korzystanie z własności rozdzielności mnożenia względem dodawania, co pozwala na uproszczenie bardziej złożonych równań. Na przykład, w równaniu $$2(x + 3) + 4 = 10$$ możemy najpierw zastosować rozdzielność, uzyskując $$2x + 6 + 4 = 10$$, co po uproszczeniu daje $$2x + 10 = 10$$. Używając tych technik, możemy skutecznie uprościć równania, co z kolei ułatwia ich późniejsze rozwiązanie.
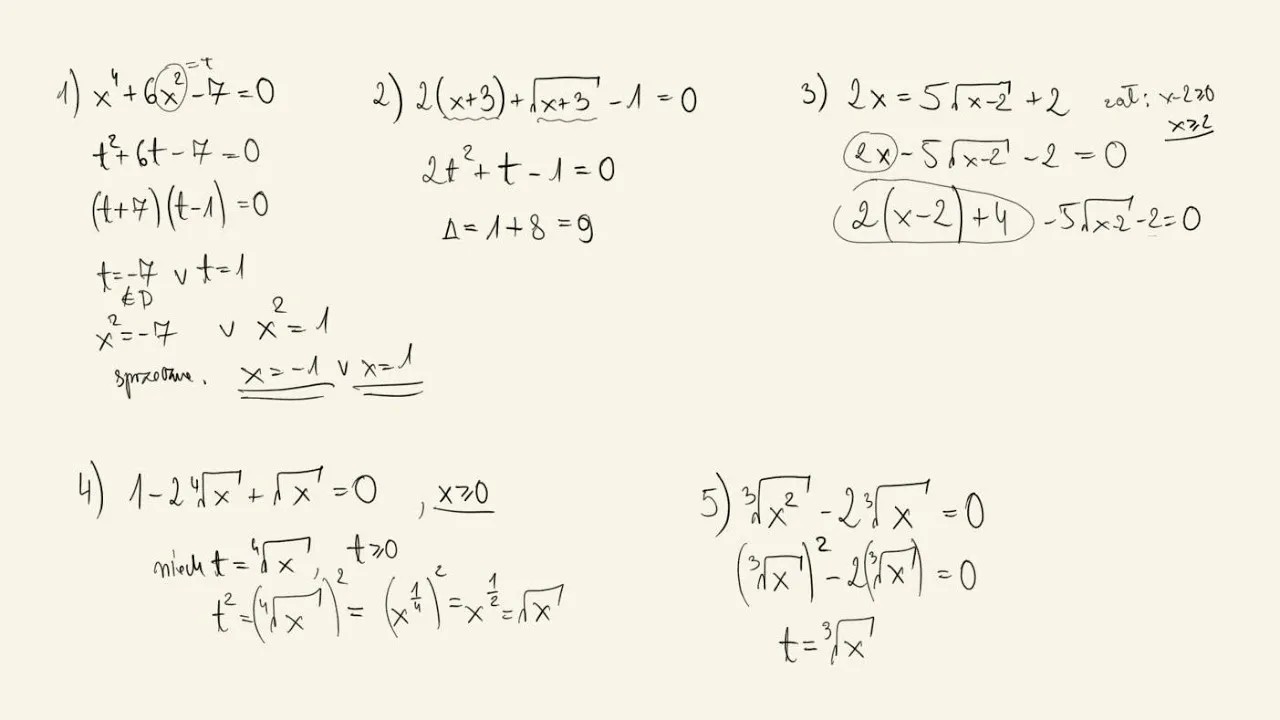
Metody specjalne: jak radzić sobie z trudniejszymi równaniami
Rozwiązywanie bardziej złożonych równań, takich jak układy równań, wymaga zastosowania specjalnych metod, w tym metody podstawiania i metody eliminacji. Metoda podstawiania polega na wyrażeniu jednej niewiadomej przez drugą i podstawieniu tego wyrażenia do drugiego równania. Z kolei metoda eliminacji polega na dodawaniu lub odejmowaniu równań, aby wyeliminować jedną z niewiadomych, co ułatwia znalezienie rozwiązania. Te techniki są szczególnie przydatne w przypadku układów dwóch lub więcej równań z dwiema lub więcej niewiadomymi.Na przykład, rozważmy układ równań: $$ \begin{cases} 2x + 3y = 6 \\ x - 4y = -2 \end{cases} $$ Najpierw możemy użyć metody podstawiania, aby wyrazić $$x$$ z drugiego równania: $$x = 4y - 2$$. Następnie podstawiamy to wyrażenie do pierwszego równania: $$2(4y - 2) + 3y = 6$$, co prowadzi do $$8y - 4 + 3y = 6$$. Uproszczając, otrzymujemy $$11y = 10$$, a zatem $$y = \frac{10}{11}$$. Wstawiając tę wartość z powrotem do równania dla $$x$$, uzyskujemy $$x = 4(\frac{10}{11}) - 2$$, co daje $$x = \frac{40}{11} - \frac{22}{11} = \frac{18}{11}$$. Tak więc rozwiązaniem układu równań jest $$x = \frac{18}{11}$$ oraz $$y = \frac{10}{11}$$.
- Układy równań liniowych: stosować metodę podstawiania lub eliminacji.
- Równania z wartością bezwzględną: rozwiązywać, rozdzielając na dwa przypadki.
- Równania kwadratowe: stosować metodę delty lub faktoryzację.
Nowoczesne narzędzia do rozwiązywania równań w praktyce
W dzisiejszych czasach, technologia odgrywa kluczową rolę w procesie rozwiązywania równań, a nowoczesne oprogramowanie matematyczne może znacznie ułatwić pracę. Programy takie jak Wolfram Alpha czy GeoGebra oferują zaawansowane funkcje, które umożliwiają użytkownikom nie tylko rozwiązywanie równań, ale także wizualizację ich graficznych reprezentacji. Dzięki tym narzędziom można szybko sprawdzić poprawność swoich rozwiązań, analizować różne przypadki oraz zrozumieć, jak zmiany parametrów wpływają na kształt wykresu.
Co więcej, uczenie maszynowe i sztuczna inteligencja stają się coraz bardziej popularne w kontekście rozwiązywania równań. Te technologie mogą analizować złożone układy równań i sugerować optymalne metody ich rozwiązania, co otwiera nowe możliwości w dziedzinach takich jak inżynieria, ekonomia czy nauki przyrodnicze. W przyszłości możemy spodziewać się jeszcze większej integracji tych narzędzi w codziennym nauczaniu matematyki, co może zrewolucjonizować sposób, w jaki uczniowie i studenci podchodzą do rozwiązywania równań.
