Znak przybliżenia w matematyce, oznaczany jako "≈", jest niezwykle ważnym symbolem, który wskazuje, że dwie wartości są bliskie sobie, ale nie są dokładnie takie same. Używany jest w sytuacjach, gdy precyzyjne wartości są trudne do osiągnięcia lub nie są konieczne. Przykłady jego zastosowania obejmują zaokrąglanie liczb oraz przybliżanie wartości niewymiernych, takich jak π (pi) czy √2. Dzięki temu symbolowi matematycy i naukowcy mogą uprościć obliczenia i komunikować wyniki w sposób zrozumiały.
W różnych dziedzinach, takich jak fizyka, inżynieria, statystyka i ekonomia, znak "≈" odgrywa kluczową rolę. Umożliwia on wyrażanie wyników pomiarów, które wiążą się z pewnym stopniem niepewności, a także raportowanie wyników analiz, gdzie dokładność nie zawsze jest najważniejsza. W niniejszym artykule przyjrzymy się bliżej znaczeniu znaku przybliżenia oraz jego zastosowaniom w praktyce.
Najważniejsze informacje:
- Znak "≈" oznacza, że dwie wartości są bliskie siebie, ale nie są identyczne.
- Jest używany w sytuacjach, gdy precyzyjne wartości są trudne do osiągnięcia.
- Symbol ten znajduje zastosowanie w matematyce, fizyce, inżynierii, statystyce i ekonomii.
- Ułatwia komunikację wyników obliczeń i pomiarów.
- Inne symbole przybliżenia, takie jak ≒, są stosowane w różnych kulturach.
Definicja znaku przybliżenia w matematyce i jego znaczenie
Znak przybliżenia w matematyce, oznaczany jako "≈", jest symbolem, który wskazuje, że dwie wartości są bliskie sobie, ale nie są identycznie takie same. To matematyczny symbol należący do zbioru znaków nierówności, składający się z dwóch falowanych linii. Używany jest w sytuacjach, gdy preczyzja jest trudna do osiągnięcia lub nie jest konieczna, co czyni go niezwykle przydatnym w wielu kontekstach matematycznych.
Znak "≈" odgrywa kluczową rolę w matematyce, szczególnie podczas zaokrąglania liczb czy przybliżania wartości niewymiernych, takich jak π (pi) czy √2. Dzięki temu symbolowi matematycy mogą wyrażać wartości, które zostały uproszczone dla łatwiejszej komunikacji. Umożliwia to lepsze zrozumienie i interpretację wyników, zwłaszcza w sytuacjach, gdzie dokładne liczby są mniej istotne.
Zrozumienie symbolu "≈" i jego zastosowanie w matematyce
Symbol "≈" jest używany w różnych kontekstach matematycznych, aby wyrazić przybliżone wartości w obliczeniach. W praktyce oznacza on, że wynik jest bliski rzeczywistej wartości, ale niekoniecznie identyczny. Na przykład, w obliczeniach związanych z pomiarami, gdzie występuje niepewność, znak ten pozwala na uproszczenie wyników bez utraty istotnych informacji. Użycie znaku "≈" jest szczególnie ważne w sytuacjach, gdy dokładność nie jest kluczowa, co pozwala na szybsze i bardziej zrozumiałe przedstawienie danych.
Różnice między przybliżeniem a dokładnymi wartościami
W matematyce istnieje istotna różnica między przybliżeniem a dokładnymi wartościami. Przybliżenie oznacza, że wartość jest bliska, ale nie identyczna, co jest szczególnie ważne w kontekście obliczeń, gdzie precyzja może być trudna do osiągnięcia. Z kolei dokładne wartości są tymi, które można w pełni określić, bez żadnych wątpliwości co do ich poprawności. Użycie znaku przybliżenia "≈" jest uzasadnione w sytuacjach, gdy wynik nie wymaga wysokiej precyzji, na przykład przy zaokrąglaniu liczb.
W praktyce, znak przybliżenia w matematyce jest stosowany, gdy dokładność nie jest kluczowa dla danego kontekstu. Na przykład, w codziennych obliczeniach, takich jak pomiar długości czy wagi, przybliżone wartości mogą być wystarczające. Zrozumienie, kiedy używać przybliżeń, a kiedy dążyć do dokładności, jest kluczowe dla efektywnego rozwiązywania problemów matematycznych i naukowych.
Praktyczne zastosowania znaku przybliżenia w naukach ścisłych
W naukach ścisłych, znak przybliżenia w matematyce odgrywa kluczową rolę w analizie danych i obliczeniach. Na przykład, w fizyce, wiele zjawisk naturalnych wymaga użycia przybliżeń, aby uprościć skomplikowane równania. Przykładem może być obliczanie wartości przyspieszenia ziemskiego, które często wyraża się jako 9,81 m/s², ale w praktycznych zastosowaniach można używać wartości 10 m/s² dla uproszczenia obliczeń. To pozwala na szybsze i łatwiejsze rozwiązywanie problemów bez utraty istotnych informacji.W inżynierii, przybliżenia są niezbędne w projektowaniu i analizie systemów. Na przykład, w budownictwie inżynierowie często posługują się przybliżonymi wartościami materiałów, aby określić wytrzymałość konstrukcji. Zastosowanie znaku "≈" w takich kontekstach pozwala na efektywne planowanie i podejmowanie decyzji, gdy dokładne pomiary są niemożliwe lub niepraktyczne. Przybliżenia w tych dziedzinach są kluczowe dla osiągnięcia funkcjonalności i bezpieczeństwa projektów.
Użycie symbolu "≈" w fizyce i inżynierii
W fizyce i inżynierii, znak przybliżenia "≈" jest niezwykle istotny, ponieważ pozwala na uproszczenie skomplikowanych obliczeń. Pomiar wielu wartości, takich jak prędkość, przyspieszenie czy siła, często wiąże się z pewnym stopniem niepewności. Na przykład, przy obliczaniu przyspieszenia ziemskiego, które wynosi około 9,81 m/s², inżynierowie mogą używać wartości przybliżonej 10 m/s², co ułatwia dalsze obliczenia. Podobnie, w przypadku prędkości światła, która wynosi 299 792 458 m/s, można ją zaokrąglić do 3 × 10^8 m/s dla uproszczenia w równaniach.
| Fizyczna stała | Przybliżona wartość |
|---|---|
| Przyspieszenie ziemskie (g) | ≈ 10 m/s² |
| Prędkość światła (c) | ≈ 3 × 10^8 m/s |
| Stała Plancka (h) | ≈ 6.63 × 10^-34 J·s |
| Ładunek elementarny (e) | ≈ 1.60 × 10^-19 C |
Rola przybliżeń w statystyce i analizie danych
W statystyce i analizie danych, przybliżenia odgrywają kluczową rolę w interpretacji wyników. Statystycy często posługują się wartościami przybliżonymi, aby uprościć złożone zestawienia danych. Na przykład, w analizach regresji, gdzie wyniki mogą być obarczone błędami pomiarowymi, przybliżone wartości pomagają w lepszym zrozumieniu ogólnych trendów. Użycie znaku "≈" pozwala na efektywne komunikowanie wyników, gdzie dokładność nie jest kluczowa, a istotne są ogólne tendencje i wzorce w danych.
Czytaj więcej: Co oznacza wykrzyknik w matematyce i jak obliczać silnię?
Wizualizacje i interpretacje znaku przybliżenia w kontekście
Wizualizacja symboli matematycznych, takich jak znak przybliżenia "≈", jest kluczowa dla zrozumienia ich zastosowania i znaczenia. Odpowiednie przedstawienie tych symboli ułatwia naukę i pozwala na szybsze przyswajanie wiedzy. W matematyce, gdzie precyzja jest istotna, umiejętność interpretacji wizualnej może pomóc w lepszym zrozumieniu złożonych równań i koncepcji. W przypadku znaku "≈", jego wizualizacja jako dwóch falowanych linii pozwala na łatwe rozróżnienie go od innych znaków matematycznych, takich jak znak równości "=" czy znak nierówności "≠".
Przykłady wizualizacji znaku przybliżenia mogą obejmować różne konteksty, w których jest on stosowany, takie jak wykresy funkcji czy równania. Wizualizacje te pomagają w przedstawieniu, jak wartości są bliskie sobie, ale nie identyczne. Umożliwiają one także lepsze zrozumienie pojęcia przybliżenia w obliczeniach matematycznych, co jest szczególnie ważne w naukach ścisłych. Dzięki tym wizualizacjom, studenci i naukowcy mogą z łatwością dostrzegać różnice między wartościami i zrozumieć, jak przybliżenia wpływają na wyniki obliczeń.
Przykłady graficzne ilustrujące zastosowanie "≈"
W kontekście matematycznym, znak przybliżenia "≈" znajduje zastosowanie w różnych równaniach i wykresach. Przykłady graficzne mogą obejmować funkcje, które przybliżają wartości, takie jak funkcje trygonometryczne czy obliczenia związane z liczbami niewymiernymi. Wizualizacje te są nie tylko pomocne w nauce, ale również w praktycznych zastosowaniach, gdzie precyzja nie jest kluczowa. Oto kilka przykładów zastosowania znaku "≈" w matematyce:
- Równanie obliczające wartość π jako ≈ 3,14 w kontekście obliczeń geometrycznych.
- Wykres funkcji sinusoidalnej, gdzie wartości są przybliżone do określonych punktów.
- Obliczenia związane z długością łuku w geometrii, gdzie używa się przybliżeń dla uproszczenia obliczeń.
Inne symbole matematyczne związane z przybliżeniem
W matematyce istnieje kilka symboli, które są związane z pojęciem przybliżenia. Oprócz znaku "≈", który wskazuje, że dwie wartości są bliskie, używa się także symbolu "≃", który oznacza przybliżoną równość w bardziej formalnym kontekście. Symbol "~" jest kolejnym przykładem, który często oznacza, że dwie wartości są asymptotycznie równe, co jest szczególnie użyteczne w analizie matematycznej. Każdy z tych symboli ma swoje specyficzne zastosowanie i kontekst, w którym jest używany, co pozwala na precyzyjniejsze wyrażanie relacji między wartościami. Zrozumienie różnic między tymi symbolami jest kluczowe dla poprawnego stosowania ich w matematyce oraz naukach ścisłych.
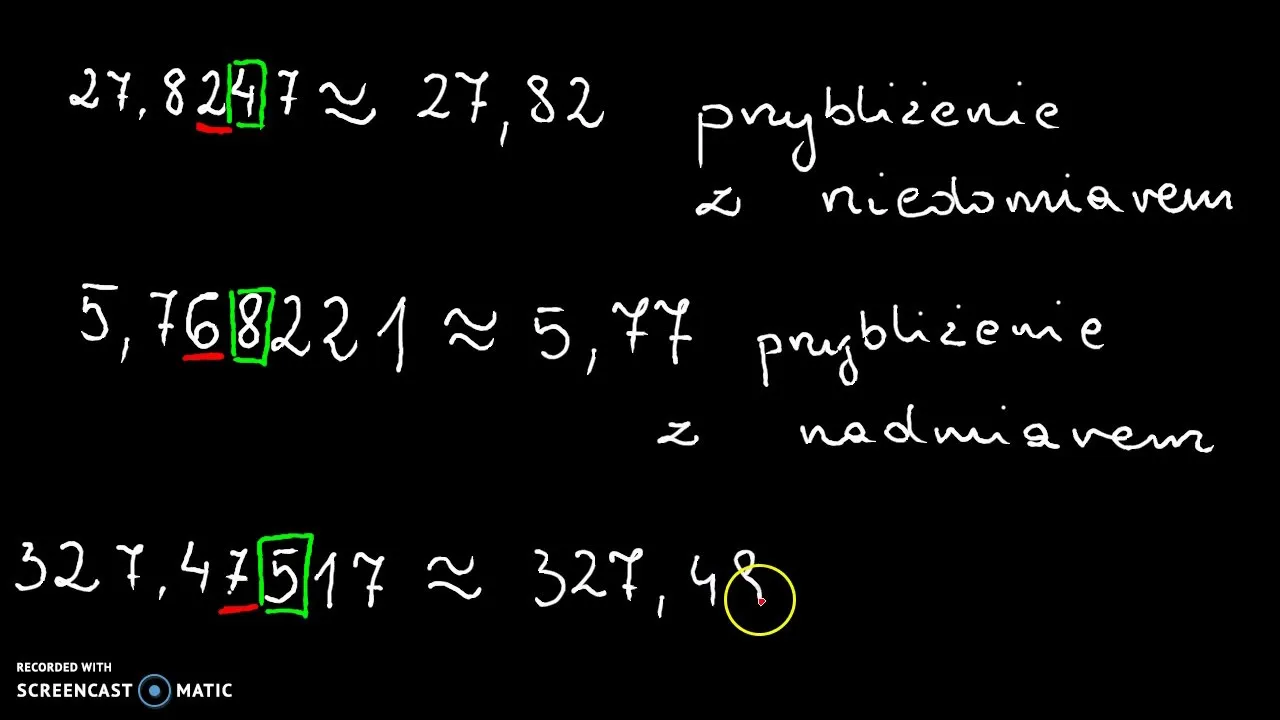
Znaczenie przybliżeń w codziennym życiu i nauce
Przybliżenia mają ogromne znaczenie w codziennym życiu oraz w różnych dziedzinach nauki. W sytuacjach, gdzie precyzyjne pomiary są trudne do uzyskania, przybliżenia pozwalają na efektywne podejmowanie decyzji. Na przykład, podczas gotowania, przepisy często wymagają przybliżonych wartości składników, co ułatwia proces przygotowywania potraw. Dzięki przybliżeniom, ludzie mogą szybko oszacować potrzebne ilości, co oszczędza czas i wysiłek.
W kontekście nauki, przybliżenia są niezbędne w badaniach i eksperymentach. W wielu dziedzinach, takich jak fizyka czy chemia, naukowcy często muszą korzystać z wartości przybliżonych, aby uzyskać sensowne wyniki. Na przykład, w badaniach nad reakcjami chemicznymi, użycie przybliżonych wartości stężeń reagentów może być wystarczające do analizy wyników. Przybliżenia pomagają w uproszczeniu złożonych obliczeń, co jest kluczowe dla postępu w nauce i technologii.
Praktyczne zastosowanie przybliżeń w nowoczesnych technologiach
W dobie nowoczesnych technologii, przybliżenia odgrywają kluczową rolę w rozwijających się dziedzinach, takich jak uczenie maszynowe i sztuczna inteligencja. Algorytmy oparte na danych często wymagają przetwarzania ogromnych zbiorów informacji, gdzie dokładne wartości mogą być nieosiągalne. W takich przypadkach przybliżenia umożliwiają modelowanie skomplikowanych zjawisk oraz predykcję wyników w sposób bardziej efektywny. Na przykład, w analizie danych dotyczących zachowań użytkowników w aplikacjach, przybliżone wartości mogą pomóc w identyfikacji trendów i wzorców, co jest kluczowe dla podejmowania decyzji biznesowych.
Co więcej, w kontekście Internetu rzeczy (IoT), przybliżenia są stosowane do optymalizacji zbierania danych z czujników. Często czujniki generują dane z pewnym poziomem niepewności, a przybliżenia pozwalają na agregację tych danych w sposób, który minimalizuje błędy i maksymalizuje użyteczność. W przyszłości, rozwój technologii przetwarzania danych i algorytmów uczenia maszynowego może jeszcze bardziej zwiększyć znaczenie przybliżeń, umożliwiając bardziej inteligentne i adaptacyjne systemy, które będą w stanie uczyć się i dostosowywać na podstawie danych przybliżonych, zamiast wymagać pełnej precyzji.




