Wartości sinusa dla kątów ostrych mieszczą się w przedziale od 0 do 1, co czyni tę funkcję niezwykle przydatną w różnych dziedzinach nauki. W artykule przyjrzymy się definicji sinusa, jego właściwościom oraz praktycznym zastosowaniom w fizyce i inżynierii, aby zrozumieć, jak ta funkcja wpływa na nasze codzienne życie i otaczający nas świat.
Kluczowe wnioski:
- Sinus definiuje stosunek długości boków w trójkącie prostokątnym.
- Wartości sinusa mieszczą się w przedziale od 0 do 1 dla kątów ostrych.
- Funkcja sinus jest okresowa, co oznacza, że jej wartości powtarzają się cyklicznie.
- Sinus znajduje zastosowanie w analizie zjawisk takich jak fale dźwiękowe i ruch harmoniczny.
- Wzór $$\sin^2\alpha + \cos^2\alpha = 1$$ jest kluczowy w trygonometrii.
Definicja sinusa i jego rola w trygonometrii
Sinus to jedna z podstawowych funkcji trygonometrycznych, która odgrywa kluczową rolę w matematyce. W kontekście trójkątów prostokątnych, sinus definiuje się jako stosunek długości boku leżącego naprzeciw kąta ostrego do długości przeciwprostokątnej. Ta definicja jest fundamentalna dla zrozumienia, jak funkcje trygonometryczne pomagają analizować relacje między kątami a bokami trójkątów. Sinus oznacza się symbolem $$\sin(\alpha)$$, gdzie $$\alpha$$ to kąt ostry.
Wartości sinusa dla kątów ostrych zawsze mieszczą się w przedziale od 0 do 1. Dla kąta 0° wartość sinusa wynosi 0, a dla kąta 90° osiąga maksimum 1. Co ważne, wartość ta jest stała dla danego kąta, niezależnie od rozmiaru trójkąta, co oznacza, że stosunek boków pozostaje niezmieniony. Dzięki temu sinus jest niezwykle użyteczny w różnych dziedzinach, takich jak inżynieria, fizyka czy nawigacja.
Zrozumienie funkcji sinus w kontekście trójkątów prostokątnych
W kontekście trójkątów prostokątnych, sinus odnosi się bezpośrednio do długości boków. W każdej konfiguracji trójkąta prostokątnego, sinus kąta ostrego $$\alpha$$ można wyrazić jako stosunek długości boku przeciwległego do długości przeciwprostokątnej. Na przykład, w trójkącie prostokątnym, jeśli bok przeciwległy ma długość 3, a przeciwprostokątna 5, to $$\sin(\alpha) = \frac{3}{5}$$.
Na powyższym diagramie trójkąta prostokątnego widać, jak sinus odnosi się do długości boków. Bok przeciwległy jest zaznaczony jako strona naprzeciw kąta, a przeciwprostokątna to najdłuższy bok trójkąta. Dzięki tej definicji, sinus staje się kluczowym narzędziem w rozwiązywaniu problemów geometrycznych i trygonometrycznych.
Jak obliczać wartość sinusa dla różnych kątów
Obliczanie wartości sinusa dla różnych kątów jest kluczowym elementem w trygonometrii. Istnieje kilka metod, które można zastosować, aby uzyskać te wartości. Dla najczęściej używanych kątów, takich jak 0°, 30°, 45°, 60° i 90°, wartości sinusa można zapamiętać lub wyznaczyć za pomocą kalkulatora lub tabeli wartości. Wartości te są stałe i można je wykorzystać w różnych obliczeniach matematycznych.
Jednym z najprostszych sposobów na obliczenie wartości sinusa jest skorzystanie z kalkulatora naukowego, który posiada funkcję sinus. Wartości te można również znaleźć w tabelach sinusa, które są dostępne w podręcznikach matematycznych. Poniżej znajduje się tabela z wartościami sinusa dla popularnych kątów, co ułatwi szybką referencję.
| Kąt (°) | Wartość sinusa |
| 0° | 0 |
| 30° | 1/2 |
| 45° | √2/2 |
| 60° | √3/2 |
| 90° | 1 |
Zasady dotyczące wartości sinusa dla kątów ostrych i prostych
Wartości sinusa dla kątów ostrych i prostych są kluczowe w trygonometrii. Sinus kątów ostrych, takich jak 30°, 45° i 60°, przyjmuje specyficzne wartości, które są stałe i mogą być łatwo zapamiętane. Na przykład, dla kąta 30° wartość sinusa wynosi 1/2, a dla kąta 45° wynosi $$\sqrt{2}/2$$. Dla kąta 60° wartość sinusa to $$\sqrt{3}/2$$. Natomiast dla kąta prostego, czyli 90°, sinus osiąga maksimum i wynosi 1. Te wartości są istotne, ponieważ pozwalają na szybkie obliczenia w różnych zastosowaniach matematycznych.
Analiza okresowości funkcji sinus w układzie współrzędnych
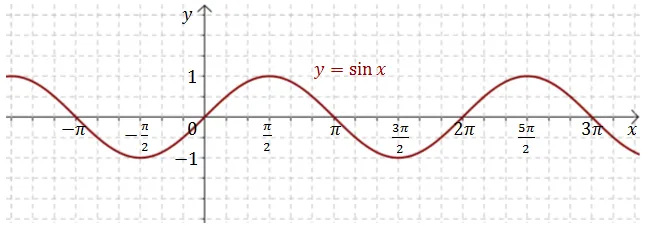
Funkcja sinus charakteryzuje się okresowością, co oznacza, że jej wartości powtarzają się w regularnych odstępach. Okres funkcji sinus wynosi $$2\pi$$ radianów, co odpowiada 360°. Graficznie, funkcja sinus przedstawia się jako falista linia, która cyklicznie wznosi się i opada, przechodząc przez wartości od -1 do 1. W układzie współrzędnych, każdy pełny cykl funkcji sinus obejmuje pełny obrót o 360°, co czyni go niezwykle użytecznym w analizie zjawisk okresowych, takich jak fale dźwiękowe czy ruch harmoniczny.
Praktyczne zastosowania sinusa w naukach ścisłych
Funkcja sinus ma wiele praktycznych zastosowań w różnych dziedzinach nauk ścisłych, w tym w fizyce i inżynierii. W kontekście fizyki, sinus jest kluczowy w analizie fal, takich jak fale dźwiękowe czy fale elektromagnetyczne. Na przykład, w teorii fal dźwiękowych, sinus jest używany do opisu amplitudy i częstotliwości fal, co pozwala na zrozumienie, jak dźwięki rozprzestrzeniają się w powietrzu. Ponadto, w inżynierii, sinus jest wykorzystywany do obliczeń związanych z ruchem harmonicznym, co jest istotne w projektowaniu maszyn i budowli.
Innym przykładem zastosowania sinusa w inżynierii jest analiza drgań w konstrukcjach. Inżynierowie używają funkcji sinus do modelowania drgań budynków i mostów, co pozwala na przewidywanie ich zachowania pod wpływem sił, takich jak wiatr czy trzęsienia ziemi. Dzięki tym obliczeniom, możliwe jest zaprojektowanie bezpiecznych i stabilnych struktur. W ten sposób, sinus nie tylko ułatwia zrozumienie zjawisk fizycznych, ale także przyczynia się do tworzenia bardziej efektywnych i bezpiecznych rozwiązań inżynieryjnych.
Rola sinusa w fizyce i inżynierii
W fizyce, sinus odgrywa kluczową rolę w opisie zjawisk falowych. Na przykład, w mechanice fal, sinus jest używany do obliczania wartości amplitudy i fazy fal dźwiękowych. W przypadku fal sinusoidalnych, które są najczęściej spotykane, ich kształt jest bezpośrednio związany z funkcją sinus. Dzięki temu inżynierowie mogą modelować i przewidywać zachowanie fal w różnych mediach, co jest niezbędne w telekomunikacji oraz technologii audio.
Sinus w analizie zjawisk okresowych, takich jak fale dźwiękowe
Funkcja sinus jest niezwykle użyteczna w analizie zjawisk okresowych, szczególnie w kontekście fal dźwiękowych. Fale dźwiękowe można opisać jako drgania cząsteczek powietrza, które rozprzestrzeniają się w formie fal sinusoidalnych. W tym przypadku, sinus pozwala na modelowanie amplitudy oraz częstotliwości dźwięku, co jest kluczowe dla zrozumienia, jak dźwięki są postrzegane przez ludzkie ucho. Na przykład, dźwięk o częstotliwości 440 Hz, co odpowiada dźwiękowi A w muzyce, można opisać za pomocą funkcji sinus, co pozwala na analizę jego właściwości akustycznych.
| Częstotliwość (Hz) | Długość fali (m) | Charakterystyka fali |
| 440 | 0.78 | Dźwięk A |
| 880 | 0.39 | Dźwięk A (wysoka oktawa) |
| 261.63 | 1.31 | Dźwięk C |
Nowe technologie w analizie fal dźwiękowych z wykorzystaniem sinusa
W dzisiejszych czasach, nowe technologie znacznie poszerzają możliwości analizy fal dźwiękowych, wykorzystując funkcję sinus do bardziej zaawansowanych zastosowań. Na przykład, w dziedzinie muzyki cyfrowej i produkcji dźwięku, inżynierowie dźwięku korzystają z algorytmów opartych na funkcji sinus do syntezowania dźwięków o wysokiej jakości. Dzięki technikom takim jak modulacja amplitudy i modulacja częstotliwości, możliwe jest tworzenie złożonych fal dźwiękowych, które mogą imitować naturalne instrumenty muzyczne.
Co więcej, analiza widma dźwięku, która również opiera się na funkcji sinus, pozwala na identyfikację i separację różnych częstotliwości w dźwięku. Dzięki temu, inżynierowie mogą lepiej dostosować dźwięki w miksie, eliminując niepożądane szumy i poprawiając jakość nagrań. W przyszłości, zastosowanie sztucznej inteligencji w analizie dźwięku może jeszcze bardziej zautomatyzować te procesy, umożliwiając bardziej precyzyjne i kreatywne podejście do produkcji dźwięku.




