Obliczanie pola trójkąta prostokątnego jest kluczową umiejętnością w matematyce, która znajduje zastosowanie w różnych dziedzinach, takich jak architektura czy inżynieria. Pole trójkąta prostokątnego można łatwo obliczyć, stosując prosty wzór: P = \frac{1}{2}ab, gdzie a i b to długości przyprostokątnych. Warto również pamiętać, że istnieje alternatywna metoda obliczania pola, wykorzystująca przeciwprostokątną oraz wysokość.
W tym artykule omówimy szczegółowo, jak stosować te wzory, a także przedstawimy praktyczne przykłady, które pomogą w zrozumieniu procesu obliczeń. Dodatkowo, zwrócimy uwagę na najczęstsze błędy, które mogą wystąpić podczas obliczania pola, oraz zaprezentujemy narzędzia online, które ułatwią tę czynność.
Kluczowe informacje:
- Wzór na pole trójkąta prostokątnego to P = \frac{1}{2}ab, gdzie a i b to długości przyprostokątnych.
- Alternatywnie, pole można obliczyć używając długości przeciwprostokątnej c oraz wysokości h jako P = \frac{1}{2}ch.
- Przykłady obliczeń pokazują, jak łatwo można obliczyć pole dla różnych wymiarów trójkątów.
- Warto unikać powszechnych błędów, takich jak nieprawidłowe pomiary lub błędne zastosowanie wzorów.
- Istnieją kalkulatory online, które automatycznie obliczają pole trójkąta, co może znacznie ułatwić pracę.
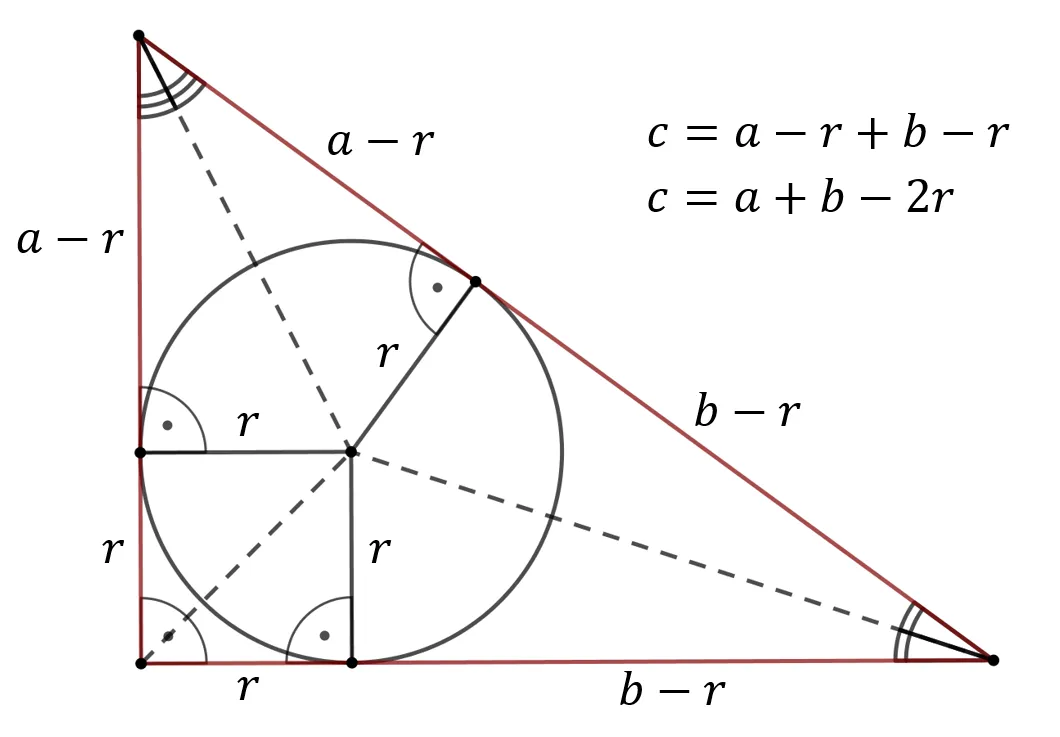
Jak obliczyć pole trójkąta prostokątnego - wzory i zasady
Obliczanie pola trójkąta prostokątnego jest kluczowym zagadnieniem w matematyce, które można zrealizować za pomocą prostego wzoru: P = \frac{1}{2}ab. W tym wzorze a i b to długości przyprostokątnych, z których jedna pełni rolę podstawy, a druga – wysokości opuszczonej na tę podstawę. Taki sposób obliczeń jest niezwykle efektywny i pozwala na szybkie uzyskanie wyniku.
Warto również pamiętać, że pole trójkąta prostokątnego można obliczyć, stosując inny wzór, który wykorzystuje przeciwprostokątną oraz wysokość. W tym przypadku wzór wygląda następująco: P = \frac{1}{2}ch, gdzie c to długość przeciwprostokątnej, a h to wysokość opuszczona na tę przeciwprostokątną. Wysokość musi być prostopadła do podstawy, co jest kluczowe dla uzyskania poprawnego wyniku.
Wzór na pole trójkąta prostokątnego - prosta formuła do zastosowania
Wzór na pole trójkąta prostokątnego, P = \frac{1}{2}ab, jest bardzo intuicyjny i łatwy do zastosowania. Derivacja tego wzoru opiera się na założeniu, że trójkąt prostokątny można traktować jako połowę prostokąta, którego boki mają długości a i b. Dlatego obliczając pole prostokąta (które wynosi ab), dzielimy je przez dwa, aby uzyskać pole trójkąta.
Warto również zauważyć, że obliczanie pola trójkąta prostokątnego z wykorzystaniem wzoru P = \frac{1}{2}ch jest równie proste, jednak wymaga znajomości wysokości. W obu przypadkach kluczowe jest, aby odpowiednio zidentyfikować długości przyprostokątnych lub wysokości, co zapewnia dokładność obliczeń.
Przykłady obliczeń pola trójkąta prostokątnego - krok po kroku
Obliczanie pola trójkąta prostokątnego można łatwo zrealizować przy użyciu wzoru P = \frac{1}{2}ab. Rozważmy pierwszy przykład: trójkąt prostokątny o przyprostokątnych długości 5 cm i 12 cm. Aby obliczyć pole, wystarczy zastosować wzór: P = \frac{1}{2} \cdot 5 \cdot 12. Po wykonaniu obliczeń, otrzymujemy P = 30 cm². To pole jest bardzo przydatne w praktyce, na przykład w budownictwie czy projektowaniu przestrzeni.
Inny przykład to trójkąt prostokątny o przyprostokątnych długości 3 cm i 4 cm. W tym przypadku również używamy wzoru: P = \frac{1}{2}ab, co daje P = \frac{1}{2} \cdot 3 \cdot 4. Po obliczeniu, uzyskujemy pole wynoszące P = 6 cm². Takie obliczenia są kluczowe w wielu dziedzinach, a znajomość kroków obliczeniowych pozwala uniknąć błędów.
| Długości przyprostokątnych (cm) | Obliczone pole (cm²) |
|---|---|
| 5 i 12 | 30 |
| 3 i 4 | 6 |
Jak obliczyć pole używając przeciwprostokątnej i wysokości
Obliczanie pola trójkąta prostokątnego można również przeprowadzić, wykorzystując przeciwprostokątną i wysokość. W tym celu stosujemy wzór: P = \frac{1}{2}ch, gdzie c to długość przeciwprostokątnej, a h to wysokość opuszczona na tę przeciwprostokątną. Wysokość musi być prostopadła do przeciwprostokątnej, co jest kluczowe dla uzyskania poprawnego wyniku. Ta metoda jest szczególnie przydatna, gdy znamy długość przeciwprostokątnej, ale nie mamy dostępu do długości przyprostokątnych.
Przykład: rozważmy trójkąt prostokątny, w którym długość przeciwprostokątnej wynosi 10 cm, a wysokość opuszczona na tę przeciwprostokątną to 6 cm. Aby obliczyć pole, podstawiamy wartości do wzoru: P = \frac{1}{2} \cdot 10 \cdot 6, co daje nam P = 30 cm². Ta metoda obliczeń jest łatwa i szybka, a także pozwala na dokładne określenie pola trójkąta.
Jak uniknąć pułapek przy obliczaniu pola trójkąta prostokątnego
Aby skutecznie obliczyć pole trójkąta prostokątnego i uniknąć typowych błędów, warto zwrócić uwagę na kilka kluczowych aspektów. Po pierwsze, zawsze upewnij się, że długości przyprostokątnych są dokładnie zmierzone i zapisane w tych samych jednostkach. Mieszanie jednostek, takich jak centymetry i metry, może prowadzić do błędnych wyników. Po drugie, sprawdź, czy wysokość jest rzeczywiście prostopadła do podstawy, ponieważ nieprawidłowe pomiary mogą znacząco wpłynąć na obliczenia.
Kolejnym krokiem jest staranne wprowadzenie wartości do wzoru. Nawet drobny błąd w obliczeniach, jak pomyłka w mnożeniu, może spowodować znaczne różnice w wyniku. Warto także korzystać z kalkulatorów online, które mogą pomóc w weryfikacji wyników. Na koniec, zawsze przelicz pole trójkąta, aby upewnić się, że jest zgodne z oczekiwaniami i odpowiada rzeczywistym wymiarom.
Jak korzystać z kalkulatorów do obliczeń geometrycznych
Korzystanie z kalkulatorów online do obliczania pola trójkąta prostokątnego jest prostym i efektywnym sposobem na uzyskanie szybkich wyników. Aby rozpocząć, wybierz kalkulator, który obsługuje obliczenia pól trójkątów. Następnie, wprowadź odpowiednie dane, takie jak długości przyprostokątnych lub przeciwprostokątnej oraz wysokości. Upewnij się, że wszystkie wartości są w tych samych jednostkach, aby uniknąć błędów. Po wprowadzeniu danych, kliknij przycisk obliczania, a kalkulator automatycznie poda wynik.
Warto również zwrócić uwagę na dodatkowe funkcje kalkulatorów, takie jak możliwość zapisywania wyników lub generowania wykresów. Niektóre kalkulatory oferują również opcje konwersji jednostek, co może być przydatne, jeśli pracujesz z różnymi systemami miar. Pamiętaj, aby zawsze sprawdzić, czy wprowadzone wartości są poprawne, zanim klikniesz przycisk obliczania, aby uzyskać jak najdokładniejsze wyniki.
- Kalkulator geometria - [geometria.pl] - łatwe w użyciu narzędzie do obliczania pól różnych figur geometrycznych.
- Kalkulator trójkąta - [trianglecalculator.com] - pozwala na obliczenie pola trójkąta na podstawie wszystkich trzech boków lub wysokości.
- Kalkulator online - [calculatorsoup.com] - wszechstronny kalkulator z możliwością obliczania pola trójkąta oraz innych figur.
Jak wykorzystać obliczenia pola trójkąta w praktyce budowlanej
Obliczanie pola trójkąta prostokątnego ma kluczowe znaczenie nie tylko w matematyce, ale także w praktycznych zastosowaniach, takich jak architektura i budownictwo. W rzeczywistych projektach budowlanych, znajomość pola trójkąta jest niezbędna do właściwego planowania przestrzeni, obliczania ilości materiałów oraz optymalizacji kosztów. Na przykład, przy budowie dachu o kształcie trójkątnym, dokładne obliczenie pola pozwala na precyzyjne określenie ilości potrzebnych dachówek, co z kolei wpływa na efektywność finansową całego projektu.
Dodatkowo, w erze cyfrowej, wiele programów CAD (Computer-Aided Design) wykorzystuje obliczenia pól trójkątów do tworzenia modeli 3D, co umożliwia inżynierom i architektom wizualizację projektów przed ich realizacją. Użycie takich narzędzi pozwala na szybsze i bardziej efektywne podejmowanie decyzji projektowych, a także na identyfikację potencjalnych problemów jeszcze przed rozpoczęciem budowy. Warto zatem zainwestować w umiejętność korzystania z tych nowoczesnych narzędzi, aby w pełni wykorzystać możliwości, jakie oferują w kontekście obliczeń geometrycznych.

