Dodawanie logarytmów to kluczowa umiejętność w matematyce, która pozwala na uproszczenie skomplikowanych obliczeń. W przypadku logarytmów o tej samej podstawie istnieje prosty wzór, który umożliwia ich dodawanie: $$\log_a(x) + \log_a(y) = \log_a(x \cdot y)$$. Oznacza to, że suma dwóch logarytmów z tą samą podstawą jest równa logarytmowi iloczynu ich argumentów. Warto zrozumieć, jak poprawnie stosować ten wzór, aby uniknąć powszechnych błędów, szczególnie gdy logarytmy mają różne podstawy.
W artykule omówimy zasady dodawania logarytmów, zarówno tych o tej samej, jak i różnych podstawach. Przedstawimy praktyczne przykłady oraz najczęstsze pułapki, które mogą prowadzić do błędnych wyników. Zrozumienie tych zasad jest nie tylko istotne w kontekście matematyki, ale także w naukach ścisłych, gdzie logarytmy odgrywają kluczową rolę.
Najistotniejsze informacje:
- Dodawanie logarytmów o tej samej podstawie można uprościć za pomocą wzoru: $$\log_a(x) + \log_a(y) = \log_a(x \cdot y)$$.
- Przykład: $$\log_2(8) + \log_2(4) = \log_2(32)$$, co oznacza, że wynik to 5, ponieważ $$2^5 = 32$$.
- Logarytmy o różnych podstawach wymagają przekształcenia do wspólnej podstawy przed dodaniem.
- Często popełnianym błędem jest próba dodawania logarytmów o różnych podstawach bez ich wcześniejszego przekształcenia.
- Logarytmy znajdują zastosowanie w wielu dziedzinach, w tym w matematyce, fizyce i inżynierii.
Jak dodawać logarytmy o tej samej podstawie - proste zasady
Dodawanie logarytmów o tej samej podstawie opiera się na prostej zasadzie, która pozwala na efektywne łączenie wartości logarytmicznych. Kluczowym wzorem w tym przypadku jest $$\log_a(x) + \log_a(y) = \log_a(x \cdot y)$$. Oznacza to, że suma dwóch logarytmów z jednakową podstawą jest równa logarytmowi iloczynu ich argumentów. Aby móc zastosować ten wzór, należy upewnić się, że logarytmy mają tę samą podstawę, co jest niezbędne do poprawnego obliczenia wyniku.
Na przykład, dodając $$\log_2(8)$$ i $$\log_2(4)$$, które mają tę samą podstawę, możemy je połączyć w następujący sposób: $$\log_2(8) + \log_2(4) = \log_2(8 \cdot 4) = \log_2(32)$$. Następnie, aby obliczyć wartość logarytmu, musimy odpowiedzieć na pytanie: do jakiej potęgi należy podnieść 2, aby otrzymać 32? Odpowiedzią jest 5, ponieważ $$2^5 = 32$$, co oznacza, że wynik to 5. Tę zasadę można stosować wielokrotnie w przypadku większej liczby logarytmów o tej samej podstawie.
Zasada dodawania logarytmów - co musisz wiedzieć
Podstawową zasadą dodawania logarytmów jest to, że muszą one mieć tę samą podstawę. W przeciwnym razie, nie można ich bezpośrednio dodać. Warto zrozumieć, że dodawanie logarytmów to proces, który opiera się na regule, która upraszcza obliczenia. Kluczowe znaczenie ma znajomość podstawowych wzorów i reguł, które pozwalają na efektywne łączenie logarytmów, co jest niezbędne w wielu dziedzinach matematyki i nauk ścisłych.
- Logarytmy o tej samej podstawie można dodawać, stosując wzór $$\log_a(x) + \log_a(y) = \log_a(x \cdot y)$$.
- W przypadku różnych podstaw, konieczne jest ich przekształcenie do wspólnej podstawy przed dodaniem.
- Przykład: $$\log_2(8) + \log_2(4)$$ prowadzi do $$\log_2(32)$$, gdzie wynik to 5.
Przykłady dodawania logarytmów o tej samej podstawie
Dodawanie logarytmów o tej samej podstawie jest prostą, ale bardzo przydatną umiejętnością. Na przykład, rozważmy dodawanie $$\log_5(25)$$ i $$\log_5(5)$$. Zgodnie z zasadą dodawania logarytmów, możemy to zapisać jako: $$\log_5(25) + \log_5(5) = \log_5(25 \cdot 5) = \log_5(125)$$. Teraz, aby obliczyć wartość logarytmu, musimy ustalić, do jakiej potęgi należy podnieść 5, aby otrzymać 125. Odpowiedzią jest 3, ponieważ $$5^3 = 125$$. Zatem wynik dodawania tych logarytmów to 3.
Kolejnym przykładem może być $$\log_3(9) + \log_3(27)$$. Zastosujmy tę samą zasadę: $$\log_3(9) + \log_3(27) = \log_3(9 \cdot 27) = \log_3(243)$$. Wartość logarytmu $$\log_3(243)$$ można obliczyć, pytając: do jakiej potęgi należy podnieść 3, aby uzyskać 243? Odpowiedzią jest 5, ponieważ $$3^5 = 243$$. Tak więc suma tych logarytmów wynosi 5.
- Przykład 1: $$\log_5(25) + \log_5(5) = \log_5(125)$$, wynik to 3.
- Przykład 2: $$\log_3(9) + \log_3(27) = \log_3(243)$$, wynik to 5.
- Obydwa przykłady ilustrują, jak dodawanie logarytmów o tej samej podstawie prowadzi do uproszczenia obliczeń.
Zmiana podstawy logarytmu - krok po kroku
Zmiana podstawy logarytmu jest kluczowym procesem, który umożliwia dodawanie logarytmów o różnych podstawach. Aby to zrobić, należy skorzystać z wzoru na zmianę podstawy, który brzmi: $$\log_a(b) = \frac{\log_c(b)}{\log_c(a)}$$, gdzie $$c$$ to nowa podstawa, na którą chcemy przekształcić logarytm. Proces ten jest istotny, ponieważ pozwala na uproszczenie obliczeń, gdy logarytmy mają różne podstawy. Najpierw wybieramy nową podstawę, a następnie obliczamy logarytmy dla argumentu i podstawy w tej nowej podstawie. Na koniec dzielimy te wartości, aby uzyskać wynik logarytmu w nowej podstawie.
Przykładowo, jeśli chcemy obliczyć $$\log_2(8)$$, możemy zmienić podstawę na 10, co daje nam $$\log_2(8) = \frac{\log_{10}(8)}{\log_{10}(2)}$$. Taka zmiana podstawy ułatwia dodawanie logarytmów, gdyż możemy teraz łączyć wartości o różnych podstawach. Zrozumienie tego procesu jest niezbędne, aby poprawnie dodawać logarytmy w różnych kontekstach matematycznych.
| Podstawa | Logarytm |
| 2 | $$\log_2(8) = 3$$ |
| 10 | $$\log_{10}(100) = 2$$ |
| 3 | $$\log_3(27) = 3$$ |
Najczęstsze błędy przy dodawaniu logarytmów - jak ich unikać
Podczas dodawania logarytmów, wiele osób popełnia powszechne błędy, które mogą prowadzić do błędnych wyników. Jednym z najczęstszych błędów jest próba dodawania logarytmów o różnych podstawach bez ich wcześniejszego przekształcenia do wspólnej podstawy. Taki krok jest niezbędny, ponieważ zasady dodawania logarytmów wymagają, aby miały one tę samą podstawę. Inny powszechny błąd to niewłaściwe stosowanie wzoru na dodawanie logarytmów, co może skutkować niepoprawnymi obliczeniami i wynikami.
Warto również zwrócić uwagę na niedokładne obliczenia przy przekształcaniu logarytmów. Często zdarza się, że uczniowie mylą wartości logarytmów, co prowadzi do dalszych błędów w obliczeniach. Aby uniknąć tych pułapek, warto regularnie ćwiczyć dodawanie logarytmów oraz sprawdzać swoje obliczenia. Używanie kalkulatorów lub programów matematycznych może również pomóc w weryfikacji wyników.
- Nieprzekształcanie logarytmów do wspólnej podstawy przed dodaniem.
- Niewłaściwe stosowanie wzoru na dodawanie logarytmów.
- Niedokładne obliczenia przy przekształcaniu logarytmów.
Typowe pułapki przy dodawaniu logarytmów - co robić źle?
Jedną z typowych pułapek jest zapominanie o konieczności zmiany podstawy, gdy logarytmy mają różne podstawy. Na przykład, dodając $$\log_2(8) + \log_3(9)$$, nie można bezpośrednio ich dodać. Należy najpierw przekształcić je do wspólnej podstawy, co wielu uczniów pomija. Innym błędem jest mylenie wartości logarytmów; na przykład, $$\log_2(4)$$ wynosi 2, a nie 4, co często prowadzi do błędnych wyników. Aby uniknąć tych pułapek, ważne jest, aby dokładnie sprawdzać swoje obliczenia i stosować odpowiednie wzory.
Czytaj więcej: Wykrzyknik w matematyce: Zrozumienie symbolu silni i jego zastosowań
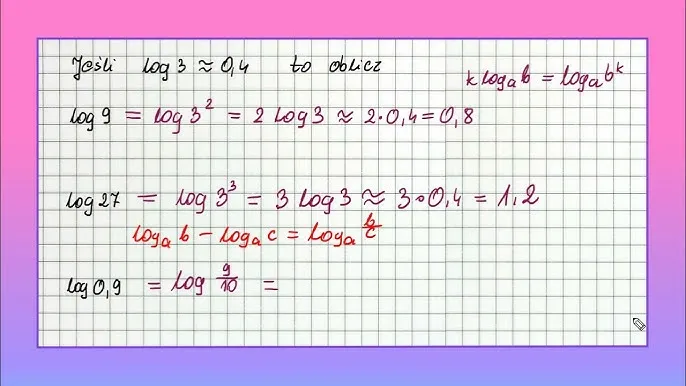
Praktyczne zastosowania dodawania logarytmów - dlaczego to ważne?
Dodawanie logarytmów ma wiele praktycznych zastosowań w różnych dziedzinach, takich jak nauki ścisłe, finanse oraz inżynieria. W naukach przyrodniczych, logarytmy są często stosowane do analizy danych, na przykład w badaniach dotyczących wzrostu populacji, gdzie zmiany w liczbie osobników mogą być modelowane za pomocą funkcji logarytmicznych. W finansach, logarytmy są używane do obliczania stóp zwrotu z inwestycji, co pozwala na lepsze zrozumienie ryzyka i potencjalnych zysków. Dzięki umiejętności dodawania logarytmów, można łatwo porównywać różne źródła danych, co jest niezwykle istotne w podejmowaniu decyzji.
W inżynierii, dodawanie logarytmów jest niezbędne w analizie sygnałów oraz w obliczeniach związanych z systemami elektronicznymi. Na przykład, w teorii sygnałów, logarytmy są używane do określenia poziomu głośności dźwięku, co jest kluczowe w projektowaniu systemów audio. Ponadto, w informatyce, logarytmy są wykorzystywane w algorytmach wyszukiwania i sortowania, co pozwala na efektywne przetwarzanie dużych zbiorów danych. Zrozumienie, jak dodawać logarytmy, ma zatem istotne znaczenie w wielu aspektach codziennego życia i pracy zawodowej.
Logarytmy w matematyce i naukach ścisłych - przykłady zastosowań
Logarytmy znajdują zastosowanie w matematyce i naukach ścisłych w wielu praktycznych sytuacjach. Na przykład, w chemii, logarytmy są używane do obliczania pH roztworów, co jest kluczowe w analizie kwasów i zasad. W biologii, logarytmy pomagają modelować wzrost bakterii, gdzie tempo wzrostu można przedstawić jako funkcję logarytmiczną. W fizyce, logarytmy są używane do analizy dźwięku i światła, gdzie intensywność tych zjawisk jest często wyrażana w skali logarytmicznej, co ułatwia porównania i obliczenia. Przykładem może być skala decybeli, która jest logarytmiczną miarą głośności dźwięku. Dzięki tym zastosowaniom, logarytmy stają się niezbędnym narzędziem w analizach naukowych i technicznych.
- Analiza danych w naukach przyrodniczych, np. wzrost populacji.
- Obliczanie stóp zwrotu w finansach.
- Modelowanie poziomu głośności dźwięku w inżynierii.
Jak logarytmy wpływają na rozwój sztucznej inteligencji
Logarytmy odgrywają kluczową rolę w rozwoju sztucznej inteligencji, zwłaszcza w kontekście analizy danych i uczenia maszynowego. W dziedzinach takich jak przetwarzanie języka naturalnego czy rozpoznawanie obrazów, logarytmy są używane do optymalizacji algorytmów, co pozwala na efektywniejsze przetwarzanie dużych zbiorów danych. Na przykład, w algorytmach klasyfikacji, logarytmy pomagają w obliczaniu prawdopodobieństw, co jest kluczowe dla podejmowania decyzji przez systemy AI. Dzięki zastosowaniu logarytmów, modele mogą lepiej uczyć się z danych, co prowadzi do bardziej precyzyjnych prognoz i wyników.W przyszłości, logarytmy mogą stać się jeszcze bardziej istotne w kontekście zaawansowanych technik, takich jak uczenie głębokie. W miarę jak technologia rozwija się, logarytmy będą miały zastosowanie w nowych dziedzinach, takich jak analiza danych w czasie rzeczywistym czy automatyzacja procesów decyzyjnych. Ich umiejętne wykorzystanie pozwoli na tworzenie bardziej zaawansowanych systemów, które będą w stanie przetwarzać i analizować dane w sposób jeszcze bardziej efektywny, co otworzy nowe możliwości w różnych branżach.

