Równoważne układy równań to kluczowy temat w matematyce, który pozwala zrozumieć, jak różne zestawy równań mogą prowadzić do tych samych rozwiązań. Aby określić, który układ równań jest równoważny, należy sprawdzić, czy mają one ten sam zbiór rozwiązań. W praktyce oznacza to, że jeśli dwa układy równań mają identyczne rozwiązania, to są one równoważne. W tym artykule przyjrzymy się, jak zdefiniować równoważne układy równań oraz jak je sprawdzić, aby uniknąć powszechnych błędów w analizie.
W kolejnych częściach omówimy różne metody weryfikacji równoważności, zarówno algebraiczne, jak i graficzne. Dowiesz się również, jakie pułapki mogą się pojawić podczas oceny równoważności układów równań, a także jak parametry mogą wpływać na równoważność. Dzięki temu artykułowi zyskasz solidne podstawy do zrozumienia tego ważnego zagadnienia.
Kluczowe informacje:
- Równoważność układów równań oznacza, że mają one ten sam zbiór rozwiązań.
- Aby sprawdzić równoważność, można podstawić rozwiązania do drugiego układu równań.
- Metody algebraiczne i graficzne są skutecznymi sposobami na weryfikację równoważności.
- Unikanie powszechnych błędów w ocenie równoważności jest kluczowe dla poprawnych analiz.
- Parametry w układach równań mogą wpływać na ich równoważność, co warto brać pod uwagę.
Jak zdefiniować równoważne układy równań? Zrozumienie podstaw
Równoważne układy równań to zestawy równań, które mają ten sam zbiór rozwiązań. Aby układy były równoważne, muszą prowadzić do tych samych wyników, niezależnie od tego, jak są zapisane. W praktyce oznacza to, że jeśli jeden układ można przekształcić w drugi, zachowując te same rozwiązania, to obydwa układy są równoważne. Zrozumienie tej koncepcji jest kluczowe w matematyce, szczególnie w kontekście równań liniowych, ponieważ pozwala na uproszczenie problemów i efektywne rozwiązywanie zadań.
Na przykład, rozważmy układ równań: $$ 2x + y = 5 \\ x - y = 1 $$ Rozwiązaniem tego układu jest para liczb $$x = 2$$, $$y = 1$$. Jeśli inny układ równań również ma to samo rozwiązanie, to jest on równoważny. Warto zauważyć, że równoważność układów równań nie zawsze jest oczywista, dlatego ważne jest, aby umieć ją zidentyfikować i zrozumieć, jakie kryteria ją definiują.
Równoważność układów równań: Co to oznacza?
Równoważność układów równań oznacza, że dwa lub więcej układów prowadzi do tych samych wartości zmiennych. W matematyce, układy równań są równoważne, gdy mają identyczny zbiór rozwiązań. Aby to określić, można wykorzystać różne metody, takie jak podstawianie lub eliminacja, ale podstawową zasadą jest sprawdzenie, czy rozwiązania są takie same. Kryteria równoważności są kluczowe, ponieważ umożliwiają uproszczenie układów równań, co jest szczególnie przydatne w rozwiązywaniu bardziej złożonych problemów matematycznych.
Przykłady układów równań równoważnych w praktyce
Równoważne układy równań są istotnym elementem w matematyce, ponieważ pozwalają na lepsze zrozumienie relacji między różnymi równaniami. Przykłady układów równań równoważnych pomagają zobrazować, jak różne zapisy mogą prowadzić do tych samych rozwiązań. Poniżej przedstawiam kilka konkretnych przykładów, które ilustrują tę koncepcję. Każdy z nich ma identyczny zbiór rozwiązań, co czyni je równoważnymi układami równań.
- Układ równań: $$ 2x + y = 5 \\ x - y = 1 $$ Rozwiązanie: $$x = 2, y = 1$$
- Układ równań: $$ 3x + 2y = 8 \\ -2x + 4y = 0 $$ Rozwiązanie: $$x = 2, y = 1$$
- Układ równań: $$ 5 - x - 2y = 4 \\ x + y = 4 $$ Rozwiązanie: $$x = 3, y = -1$$
- Układ równań: $$ m(2x - y) = 10 \\ -3x - (2n + 1)y = 5 $$ Równoważność dla $$m = -3$$ i $$n = 6.5$$ lub $$m = 3$$ i $$n = 6.5$$.
Metody algebraiczne do weryfikacji równoważności
Metody algebraiczne są kluczowym narzędziem w określaniu, czy dwa układy równań są równoważne. Wykorzystują one różne techniki, takie jak podstawianie, eliminacja oraz przekształcanie równań, aby sprawdzić, czy układy prowadzą do tych samych rozwiązań. Na przykład, można przekształcić jeden układ równań w taki sposób, aby uzyskać drugi, co potwierdzi ich równoważność. Ważne jest, aby pamiętać, że każdy krok w tych metodach musi być dokładny, aby uniknąć błędów w ocenie równoważności.
Jedną z popularnych technik jest metoda podstawiania, w której rozwiązanie jednej zmiennej jest wstawiane do drugiego równania. Ta technika pozwala na uproszczenie układów i łatwiejsze odnalezienie wartości niewiadomych. Na przykład, jeśli mamy układ równań, w którym z jednego równania wyznaczamy jedną zmienną, a następnie podstawiamy ją do drugiego równania, możemy szybko sprawdzić, czy oba układy są równoważne.
Wykorzystanie graficznych metod do analizy układów
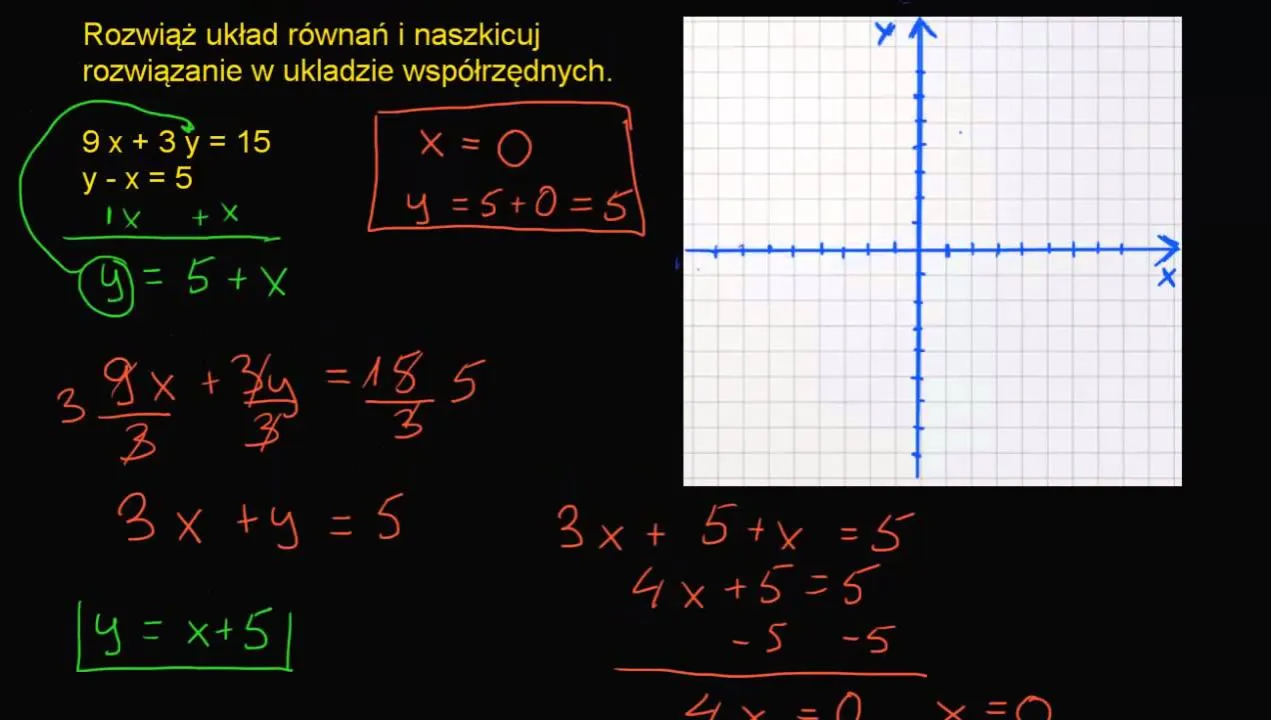
Graficzne metody analizy układów równań są skutecznym sposobem na wizualizację ich równoważności. Poprzez rysowanie wykresów, możemy łatwo zobaczyć, czy różne układy równań przecinają się w tych samych punktach, co oznacza, że mają identyczne rozwiązania. Wykresy równań liniowych przedstawiają proste na płaszczyźnie, a ich przecięcia wskazują na wartości zmiennych, które są rozwiązaniami układów. Ta metoda jest szczególnie pomocna w przypadku układów z dwiema niewiadomymi.Interpreting the results from graphical methods involves analyzing the points of intersection. Jeśli dwie linie na wykresie przecinają się w jednym punkcie, oznacza to, że układy mają jedno wspólne rozwiązanie. W przypadku, gdy linie są równoległe, układy nie mają rozwiązań, a jeśli pokrywają się, to mają nieskończoną liczbę rozwiązań. Takie analizy są pomocne w wizualizacji i lepszym zrozumieniu relacji między układami równań.
Jakie pułapki unikać przy analizie równoważności? Kluczowe błędy
Podczas analizy równoważności układów równań, istnieje wiele pułapek, które mogą prowadzić do błędnych wniosków. Wielu uczniów i osób uczących się matematyki popełnia typowe błędy, które mogą zniekształcić ich zrozumienie tematu. Zrozumienie tych pułapek jest kluczowe dla poprawnej oceny równoważności. W tej sekcji omówimy najczęstsze błędy oraz pułapki, które mogą się pojawić podczas pracy z układami równań.Jednym z powszechnych błędów jest nieprawidłowe podstawianie wartości do równań. Czasami uczniowie zakładają, że rozwiązanie jednego równania automatycznie sprawdzi się w drugim, co nie zawsze jest prawdą. Ważne jest, aby upewnić się, że każde równanie jest spełnione przez proponowane rozwiązanie. Kolejnym częstym błędem jest mylenie równoważności z podobieństwem. Układy równań mogą wyglądać podobnie, ale to nie oznacza, że są równoważne. Kluczowe jest, aby zawsze sprawdzać zbiór rozwiązań, a nie tylko wizualne podobieństwo równań.
Najczęstsze błędy w ocenie równoważności układów
W trakcie oceny równoważności układów równań, uczniowie często popełniają konkretne błędy, które mogą prowadzić do błędnych wniosków. Znajomość tych błędów może pomóc w uniknięciu nieporozumień i poprawie umiejętności analizy matematycznej. Oto kilka najczęstszych błędów, które warto mieć na uwadze:
- Nieprawidłowe podstawianie wartości do równań, co prowadzi do błędnych wniosków.
- Mylenie równoważności z podobieństwem układów równań.
- Brak uwzględnienia wszystkich zmiennych w układzie równań przy ocenie równoważności.
- Zakładanie, że układy równań są równoważne tylko na podstawie ich wizualnego podobieństwa.
Rola parametrów w równoważności układów równań
Parametry w układach równań odgrywają kluczową rolę w określaniu ich równoważności. Wprowadzenie parametrów do równań może zmieniać zbiór rozwiązań i wpływać na to, czy układy są równoważne. Na przykład, gdy w równaniu pojawiają się zmienne zależne od parametrów, zmieniają się warunki, w jakich układ równań może mieć wspólne rozwiązania. Warto zrozumieć, jak różne wartości parametrów mogą prowadzić do różnych układów równoważnych lub nie równoważnych.
Przykładem może być układ równań z parametrami, w którym różne wartości parametrów prowadzą do różnych zbiorów rozwiązań. Na przykład, układ równań: $$ m(2x - y) = 10 \\ -3x - (2n + 1)y = 5 $$ ma różne wartości parametrów $$m$$ i $$n$$, które mogą wpływać na to, czy układ jest równoważny innemu układowi. W przypadku, gdy $$m = -3$$ i $$n = 6.5$$ lub $$m = 3$$ i $$n = 6.5$$, układy te są równoważne. Poniżej znajduje się tabela ilustrująca różne parametry i ich wpływ na równoważność układów równań.
| Parametry (m, n) | Układ równań | Równoważność |
| -3, 6.5 | $$ -3(2x - y) = 10 \\ -3x - (2(6.5) + 1)y = 5 $$ | Równoważny |
| 3, 6.5 | $$ 3(2x - y) = 10 \\ -3x - (2(6.5) + 1)y = 5 $$ | Równoważny |
| 1, 2 | $$ 1(2x - y) = 10 \\ -3x - (2(2) + 1)y = 5 $$ | Nie równoważny |
Jak wykorzystać równoważność układów równań w praktyce
Równoważność układów równań ma szerokie zastosowanie w różnych dziedzinach, od inżynierii po ekonomię. Umiejętność identyfikacji równoważnych układów równań może znacząco uprościć proces rozwiązywania złożonych problemów, oszczędzając czas i zasoby. Na przykład, w inżynierii, gdy projektanci muszą przeprowadzić analizy strukturalne, mogą używać równoważnych układów równań, aby uprościć obliczenia i uzyskać szybsze wyniki. Dzięki temu możliwe jest łatwiejsze modelowanie systemów, co prowadzi do bardziej efektywnych rozwiązań.
W przyszłości, rozwój narzędzi komputerowych i algorytmów opartych na sztucznej inteligencji może zrewolucjonizować sposób, w jaki analizujemy równoważność układów równań. Dzięki automatyzacji procesu weryfikacji równoważności, inżynierowie i naukowcy będą mogli skupić się na bardziej skomplikowanych aspektach swoich projektów, pozostawiając rutynowe obliczenia maszynom. Taki postęp może prowadzić do bardziej innowacyjnych i złożonych rozwiązań w różnych dziedzinach nauki i technologii.

