Kluczowe wnioski:
- Układ równań z dwiema niewiadomymi składa się z dwóch równań i dwóch niewiadomych.
- Najczęściej stosowane metody to: metoda podstawiania i metoda przeciwnych współczynników.
- Metoda graficzna pozwala na wizualizację równań i interpretację punktów przecięcia.
- Metoda wyznaczników umożliwia analizę liczby rozwiązań układu równań.
- Każda z metod ma swoje zalety i zastosowanie w zależności od charakteru problemu.
Jak rozwiązać układ równań z 2 niewiadomymi - podstawowe metody
Rozwiązywanie układów równań z dwiema niewiadomymi jest kluczową umiejętnością w matematyce, która ma zastosowanie w wielu dziedzinach, takich jak inżynieria, ekonomia czy nauki przyrodnicze. Aby znaleźć rozwiązanie takiego układu, potrzebujemy dwóch równań z tymi samymi niewiadomymi, co pozwala nam wyznaczyć wartości x i y, które spełniają oba równania jednocześnie. Właściwe zrozumienie metod rozwiązywania tych układów jest niezbędne dla każdego, kto chce skutecznie poruszać się w świecie matematyki.
W artykule omówimy dwie najpopularniejsze metody rozwiązywania układów równań: metodę podstawiania oraz metodę przeciwnych współczynników. Metoda podstawiania polega na wyznaczeniu jednej z niewiadomych z jednego równania i podstawieniu jej do drugiego, co pozwala na rozwiązanie układu. Z kolei metoda przeciwnych współczynników polega na przekształceniu równań w taki sposób, aby jedna z niewiadomych została wyeliminowana, co prowadzi do prostszego równania z jedną niewiadomą. Obie metody mają swoje zalety i zastosowanie, w zależności od charakterystyki danego układu równań.Metoda podstawiania - krok po kroku do rozwiązania
Metoda podstawiania to jedna z najprostszych i najczęściej stosowanych metod rozwiązywania układów równań. Polega ona na wyznaczeniu jednej z niewiadomych z jednego równania, a następnie podstawieniu jej do drugiego równania. Na przykład, jeśli mamy układ równań:
1) 2x + y = 10
2) x - y = 2
Możemy wyznaczyć y z pierwszego równania: y = 10 - 2x. Następnie podstawiamy to wyrażenie do drugiego równania, co daje nam równanie z jedną niewiadomą: x - (10 - 2x) = 2. Rozwiązując to równanie, znajdziemy wartość x, a następnie podstawimy ją z powrotem, aby znaleźć y.
Korzyści płynące z zastosowania metody podstawiania to jej prostota oraz intuicyjność. Jest to metoda, która często pozwala na szybkie uzyskanie rozwiązania, zwłaszcza w przypadku prostych równań. Ponadto, metoda ta jest bardzo przydatna, gdy jedno z równań jest łatwe do przekształcenia i wyznaczenia jednej z niewiadomych.
Metoda przeciwnych współczynników - szybkie rozwiązywanie równań
Metoda przeciwnych współczynników to jedna z efektywnych technik rozwiązywania układów równań z dwiema niewiadomymi. Jej głównym celem jest przekształcenie równań tak, aby po dodaniu lub odjęciu ich stronami jedna z niewiadomych została wyeliminowana. Ta metoda jest szczególnie przydatna, gdy mamy do czynienia z równaniami, które można łatwo przekształcić, aby uzyskać przeciwne współczynniki.
Rozważmy przykład, aby lepiej zrozumieć, jak działa ta metoda. Mamy układ równań:
1) 3x + 2y = 16
2) 5x - 2y = 4
8x = 20, co daje nam x = 2. Następnie podstawiamy tę wartość do jednego z równań, aby znaleźć y. Wstawiając x do pierwszego równania:
3(2) + 2y = 16, co prowadzi do 6 + 2y = 16, a więc 2y = 10 i y = 5.
Metoda przeciwnych współczynników ma wiele zalet. Przede wszystkim jest szybka i skuteczna, zwłaszcza w przypadku układów, w których współczynniki są łatwe do przekształcenia. Dzięki tej metodzie można szybko dotrzeć do rozwiązania, co czyni ją popularnym wyborem wśród uczniów i studentów. Dodatkowo, pozwala na łatwe sprawdzenie poprawności uzyskanych wyników, ponieważ można je podstawić z powrotem do oryginalnych równań.
| Zaleta | Opis |
| Szybkość | Możliwość szybkiego uzyskania rozwiązania w prostych układach. |
| Łatwość | Proste przekształcenia równań umożliwiają eliminację niewiadomych. |
| Weryfikacja | Łatwość sprawdzenia poprawności uzyskanych wartości. |
Jak narysować wykresy równań w układzie współrzędnych
Aby narysować wykresy równań w układzie współrzędnych, należy najpierw przekształcić każde równanie do postaci y = mx + b, gdzie m to nachylenie prostej, a b to punkt przecięcia z osią y. Przy pomocy tej postaci możemy łatwo określić, jak będzie wyglądał wykres. Na przykład, dla równania 2x + 3y = 6, przekształcamy je do postaci y = -2/3x + 2, co pozwala nam na łatwe narysowanie prostej w układzie współrzędnych.
Po przekształceniu równań, kolejnym krokiem jest zaznaczenie punktów na wykresie. Należy wybrać kilka wartości x, obliczyć odpowiadające im wartości y i zaznaczyć te punkty na płaszczyźnie. Następnie łączymy je linią prostą. Dla wspomnianego wcześniej równania, możemy wybrać wartości x = 0, 1, 2, co daje nam odpowiednio punkty (0, 2), (1, 4/3) i (2, 0). Łącząc te punkty, uzyskujemy wykres prostej, który reprezentuje dane równanie.
Interpretacja punktów przecięcia - jedno, nieskończoność czy brak rozwiązań
Interpretacja punktów przecięcia wykresów równań jest kluczowa dla zrozumienia, jakie rozwiązania ma dany układ równań. Istnieją trzy główne scenariusze, które należy wziąć pod uwagę. Pierwszy z nich to sytuacja, w której proste przecinają się w jednym punkcie. Oznacza to, że układ równań ma jedno unikalne rozwiązanie, co jest przypadkiem tzw. układu oznaczonego.
Drugi scenariusz to sytuacja, w której proste są równoległe i nigdy się nie przecinają. W tym przypadku układ równań nie ma rozwiązań, co nazywamy układem sprzecznym. Ostatni scenariusz to sytuacja, w której proste pokrywają się, co oznacza, że układ ma nieskończenie wiele rozwiązań. Taki układ nazywamy układem nieoznaczonym. Zrozumienie tych scenariuszy pozwala na skuteczną analizę rozwiązań układów równań z dwiema niewiadomymi.
| Typ układu | Opis |
| Układ oznaczony | Proste przecinają się w jednym punkcie, jedno unikalne rozwiązanie. |
| Układ sprzeczny | Proste są równoległe, brak rozwiązań. |
| Układ nieoznaczony | Proste pokrywają się, nieskończoność rozwiązań. |
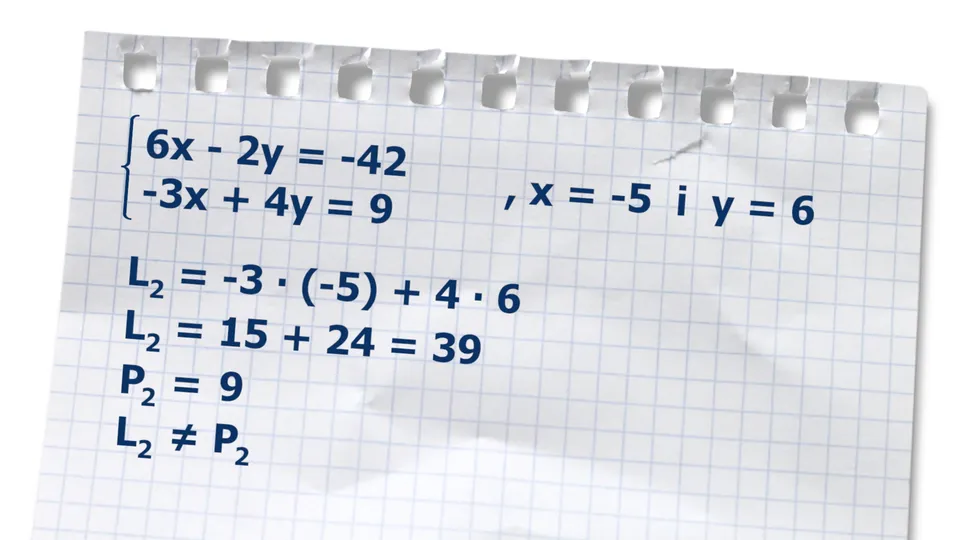
Metoda wyznaczników - zaawansowane podejście do równań
Metoda wyznaczników to zaawansowane podejście do rozwiązywania układów równań z dwiema niewiadomymi, które wykorzystuje wyznaczniki do określenia liczby rozwiązań układu. Wyznaczniki są wartościami liczbowymi, które można obliczyć dla macierzy, a ich analiza pozwala na szybkie zrozumienie, czy układ równań ma jedno, nieskończoność czy brak rozwiązań. Metoda ta jest szczególnie przydatna w przypadku większych układów równań, gdzie inne metody mogą być mniej efektywne.
Aby obliczyć wyznacznik dla układu równań z dwiema niewiadomymi, należy najpierw zapisać równania w postaci macierzy. Dla układu równań:
1) 2x + 3y = 5
2) 4x - y = 11
Możemy stworzyć macierz główną, gdzie współczynniki x i y są umieszczone w pierwszej i drugiej kolumnie, a stałe w trzeciej kolumnie. Wyznacznik główny (W) obliczamy według wzoru:
W = |A| = (2 * -1) - (3 * 4) = -2 - 12 = -14.
Jeśli wyznacznik jest różny od zera (W ≠ 0), to układ ma jedno rozwiązanie. W przeciwnym przypadku, jeśli W = 0, musimy obliczyć wyznaczniki pomocnicze W_x i W_y, aby określić, czy układ jest sprzeczny, czy nieoznaczony.
Obliczanie wyznaczników - jak to zrobić poprawnie
Obliczanie wyznaczników dla systemu 2x2 jest stosunkowo proste. Używamy wzoru dla macierzy 2x2, który wygląda następująco:
Jeśli mamy macierz:
| a b |
| c d |
to wyznacznik obliczamy jako: W = ad - bc.
Przykład: Dla macierzy | 2 3 |
| 4 -1 |
obliczamy wyznacznik:
W = (2 * -1) - (3 * 4) = -2 - 12 = -14.
Wartość -14 oznacza, że układ równań ma jedno rozwiązanie. W przypadku, gdybyśmy mieli inną macierz, na przykład | 2 3 |
| 4 6 |, wyznacznik wyniósłby 0, co wskazuje, że układ jest sprzeczny lub nieoznaczony.
| Typ wyznacznika | Interpretacja |
| W ≠ 0 | Układ ma jedno unikalne rozwiązanie. |
| W = 0, W_x ≠ 0 | Układ jest sprzeczny, brak rozwiązań. |
| W = 0, W_x = 0, W_y = 0 | Układ jest nieoznaczony, nieskończoność rozwiązań. |
Analiza wyników wyznaczników - co mówią o układzie równań
Analiza wyników wyznaczników jest kluczowa dla zrozumienia, jakie rozwiązania ma dany układ równań. Istnieją trzy główne scenariusze, które można zidentyfikować na podstawie wartości wyznaczników. Po pierwsze, jeśli główny wyznacznik (W) jest różny od zera (W ≠ 0), oznacza to, że układ ma jedno unikalne rozwiązanie. Taki układ nazywamy układem oznaczonym.
Po drugie, jeśli wyznacznik jest równy zero (W = 0), musimy zbadać wyznaczniki pomocnicze W_x i W_y. Jeżeli przynajmniej jeden z nich jest różny od zera, układ jest sprzeczny, co oznacza, że nie ma rozwiązań. W przeciwnym przypadku, jeśli oba wyznaczniki pomocnicze są równe zero, mamy do czynienia z układem nieoznaczonym, co oznacza, że istnieje nieskończoność rozwiązań.
Przykłady scenariuszy
Rozważmy kilka przykładów, aby lepiej zrozumieć te scenariusze. Pierwszy przykład: dla układu równań:
1) 2x + 3y = 6
2) 4x + 6y = 12
Wyznacznik główny W = 0, co sugeruje, że układ jest nieoznaczony, ponieważ równania są proporcjonalne i reprezentują tę samą prostą.
Drugi przykład: dla układu równań:
1) x + y = 10
2) 2x - y = 4
Obliczając wyznacznik, otrzymujemy W ≠ 0, co oznacza, że ten układ ma jedno unikalne rozwiązanie.
| Scenariusz | Opis |
| Układ oznaczony | W ≠ 0; jedno unikalne rozwiązanie. |
| Układ sprzeczny | W = 0, W_x ≠ 0; brak rozwiązań. |
| Układ nieoznaczony | W = 0, W_x = 0, W_y = 0; nieskończoność rozwiązań. |
Jak wykorzystać metody rozwiązywania równań w praktyce codziennej
Umiejętność rozwiązywania układów równań z dwiema niewiadomymi ma wiele praktycznych zastosowań w codziennym życiu oraz w różnych dziedzinach zawodowych. Na przykład, inżynierowie często wykorzystują te metody do optymalizacji procesów produkcyjnych, gdzie muszą obliczyć odpowiednie proporcje surowców, aby zminimalizować koszty, a jednocześnie spełnić wymagania jakościowe. W ekonomii, analitycy mogą stosować układy równań do przewidywania zachowań rynkowych, modelując zależności między różnymi zmiennymi, takimi jak popyt i podaż.
Co więcej, w erze cyfrowej, narzędzia programistyczne i aplikacje mobilne zaczynają integrować metody rozwiązywania równań, co umożliwia użytkownikom łatwe i szybkie obliczenia. Na przykład, aplikacje do planowania budżetu mogą korzystać z układów równań, aby pomóc użytkownikom zrozumieć, jak różne wydatki wpływają na ich oszczędności. Zrozumienie i umiejętność stosowania tych metod nie tylko poprawia zdolności analityczne, ale również otwiera drzwi do innowacyjnych rozwiązań w różnych branżach.

