Oprócz tych metod, omówimy również zastosowanie wyznaczników w kontekście układów równań oraz ich interpretację. Dzięki tym informacjom, czytelnik zdobędzie wiedzę na temat różnorodnych sposobów rozwiązywania równań z dwiema niewiadomymi oraz ich graficznej reprezentacji, co pozwoli na lepsze zrozumienie tego tematu.
Kluczowe informacje:
- Równania z dwiema niewiadomymi mają nieskończoną liczbę rozwiązań, które tworzą linię prostą.
- Metoda podstawiania polega na wyznaczeniu jednej zmiennej jako funkcji drugiej.
- Metoda przeciwnych współczynników umożliwia eliminację jednej zmiennej przez dodanie równań.
- Wyznaczniki są użyteczne w rozwiązywaniu układów równań liniowych.
- Graficzna reprezentacja równań pozwala na wizualizację punktów przecięcia, które reprezentują rozwiązania układu.
Jak obliczyć równanie z dwiema niewiadomymi - podstawowe metody
Rozwiązywanie równań z dwiema niewiadomymi to kluczowa umiejętność w matematyce. Istnieją różne metody, które pozwalają na znalezienie wartości zmiennych, które spełniają dane równania. Dwie z najczęściej stosowanych metod to metoda podstawiania oraz metoda przeciwnych współczynników. Każda z tych metod ma swoje zalety i może być stosowana w zależności od konkretnego układu równań.
Metoda podstawiania polega na wyznaczeniu jednej zmiennej jako funkcji drugiej. Natomiast metoda przeciwnych współczynników polega na przekształceniu równań w taki sposób, aby umożliwić eliminację jednej z niewiadomych. Obie metody prowadzą do znalezienia wartości zmiennych, które są kluczowe dla rozwiązania układu równań.Metoda podstawiania - krok po kroku do rozwiązania
Metoda podstawiania jest jedną z najprostszych technik rozwiązywania równań z dwiema niewiadomymi. Polega na wyznaczeniu jednej zmiennej w jednym równaniu i podstawieniu jej do drugiego równania. Na przykład, jeśli mamy równania: 2x + 3y = 6 oraz x = 2 - y, możemy zastąpić x w pierwszym równaniu, co pozwoli nam znaleźć wartość y.
Przykład krok po kroku: Rozważmy układ równań: y = 2x + 1 oraz 3x + 2y = 12. Najpierw podstawiamy y z pierwszego równania do drugiego: 3x + 2(2x + 1) = 12. Rozwiązując to równanie, otrzymujemy 3x + 4x + 2 = 12, co upraszcza się do 7x = 10. Stąd x = 10/7. Następnie podstawiamy tę wartość z powrotem do pierwszego równania, aby obliczyć y.
Podsumowując, metoda podstawiania jest skuteczna i prosta, ale wymaga staranności w obliczeniach. Kluczowe jest, aby poprawnie wyznaczyć jedną zmienną i dokładnie podstawiać ją do drugiego równania. Dzięki tej metodzie można szybko znaleźć rozwiązania układów równań z dwiema niewiadomymi.
- Upewnij się, że poprawnie wyznaczasz zmienną, którą podstawiasz.
- Sprawdzaj obliczenia na każdym etapie, aby uniknąć błędów.
- Nie pomijaj kroków, nawet jeśli wydają się oczywiste - każdy etap jest ważny.
Metoda przeciwnych współczynników - efektywne podejście
Metoda przeciwnych współczynników to jedna z najskuteczniejszych technik rozwiązywania układów równań z dwiema niewiadomymi. Polega na przekształceniu równań w taki sposób, aby współczynniki przy jednej z niewiadomych były przeciwne. Dzięki temu możemy dodać oba równania, eliminując jedną zmienną i łatwiej znaleźć wartość drugiej. Jest to szczególnie przydatne, gdy równania są łatwe do przekształcenia.
Przykład zastosowania metody przeciwnych współczynników: Rozważmy układ równań: 2x + 3y = 12 oraz 4x - 3y = 8. Aby zastosować tę metodę, możemy dodać oba równania. W tym celu najpierw upewniamy się, że współczynniki przy y są przeciwne. W naszym przypadku są one już takie, więc dodajemy równania: (2x + 3y) + (4x - 3y) = 12 + 8. Po uproszczeniu otrzymujemy 6x = 20, co prowadzi do x = \frac{20}{6} = \frac{10}{3}. Następnie tę wartość podstawiamy do jednego z równań, aby obliczyć y.
Metoda przeciwnych współczynników ma wiele zalet. Jest szybka i efektywna, zwłaszcza w przypadku prostych układów równań. Pozwala na łatwe wyeliminowanie zmiennych i szybkie dojście do rozwiązania. Warto jednak pamiętać, że wymaga umiejętności przekształcania równań, co może być wyzwaniem dla niektórych uczniów.
| Metoda | Zalety | Wady |
|---|---|---|
| Podstawianie | Łatwa w zrozumieniu, dobra dla prostych równań | Może być czasochłonna przy skomplikowanych układach |
| Przeciwnych współczynników | Szybka i efektywna, dobrze działa przy prostych układach | Wymaga umiejętności przekształcania równań |
Jak obliczyć wyznacznik macierzy dla równań liniowych
Aby obliczyć wyznacznik macierzy, musimy najpierw zrozumieć, jak zbudowana jest macierz. Wyznacznik jest liczbową wartością, która może być obliczona dla macierzy kwadratowej. Dla macierzy 2x2, wyznacznik można obliczyć za pomocą wzoru: det(A) = ad - bc, gdzie macierz A ma postać:
| a b |
| c d |
Dla większych macierzy, takich jak 3x3, wyznacznik oblicza się przez rozwinięcie względem dowolnego wiersza lub kolumny. W przypadku macierzy 3x3, wyznacznik można obliczyć według wzoru:
det(A) = a(ei - fh) - b(di - fg) + c(dh - eg), gdzie macierz A ma postać:
| a b c |
| d e f |
| g h i |
Interpretacja wyników wyznaczników w kontekście równań
Wynik wyznacznika ma kluczowe znaczenie w kontekście układów równań. Jeśli wyznacznik macierzy jest równy zero, oznacza to, że układ równań jest nieoznaczony lub sprzeczny, co wskazuje na nieskończoną liczbę rozwiązań lub ich brak. W przeciwnym razie, gdy wyznacznik jest różny od zera, układ równań ma jedno unikalne rozwiązanie.
Na przykład, w przypadku układu równań, który ma macierz o wyznaczniku równym zero, może to oznaczać, że równania są liniowo zależne, co prowadzi do nieskończonej liczby rozwiązań. Z drugiej strony, gdy wyznacznik jest różny od zera, możemy być pewni, że istnieje jedno konkretne rozwiązanie, które można znaleźć przy użyciu różnych metod, takich jak metoda podstawiania czy metoda przeciwnych współczynników.
| Wartość wyznacznika | Interpretacja |
|---|---|
| 0 | Układ równań jest nieoznaczony lub sprzeczny |
| Różny od 0 | Układ równań ma jedno unikalne rozwiązanie |
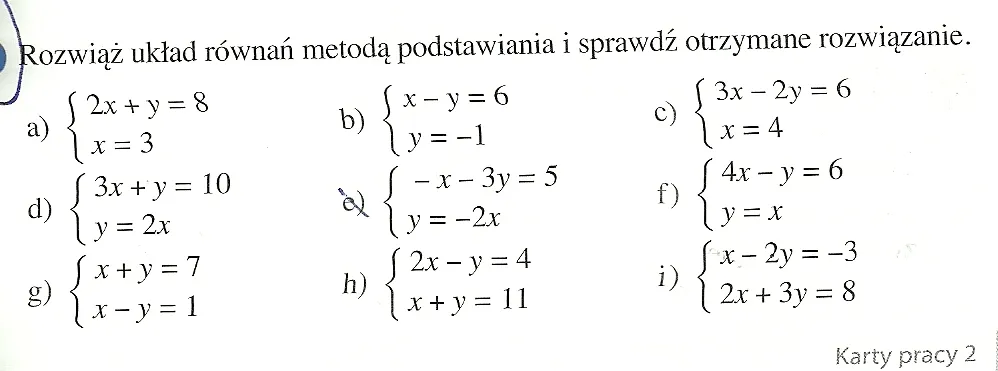
Graficzna reprezentacja równań z dwiema niewiadomymi - wizualizacja rozwiązań
Graficzna reprezentacja równań z dwiema niewiadomymi jest kluczowym narzędziem w matematyce, które pozwala na wizualizację rozwiązań. Aby narysować wykres równania, należy najpierw przekształcić je do postaci, którą można łatwo zwizualizować, na przykład do postaci y = mx + b, gdzie m to nachylenie, a b to punkt przecięcia z osią y. Po przekształceniu równania, można wyznaczyć kilka punktów, które następnie zostaną naniesione na płaszczyznę kartezjańską.
Ważnym aspektem graficznej reprezentacji równań jest analiza punktów przecięcia. Punkty te reprezentują rozwiązania układu równań, a ich interpretacja jest kluczowa dla zrozumienia relacji między równaniami. Na przykład, jeśli dwa wykresy przecinają się w jednym punkcie, oznacza to, że układ równań ma jedno unikalne rozwiązanie. Jeśli wykresy są równoległe, układ nie ma rozwiązań, a jeśli pokrywają się, istnieje nieskończona liczba rozwiązań.Jak narysować wykres równania liniowego - praktyczne wskazówki
Aby narysować wykres równania liniowego, warto zacząć od przekształcenia równania do postaci y = mx + b. Następnie, wybierz kilka wartości dla zmiennej x, oblicz odpowiadające im wartości y i zapisz te punkty. Na przykład, dla równania y = 2x + 1, można wybrać wartości x takie jak -1, 0, 1, a następnie obliczyć y: dla x = -1, y = -1; dla x = 0, y = 1; dla x = 1, y = 3.
Po zdobyciu punktów, należy je nanieść na wykres i połączyć linią prostą. W przypadku równania y = 2x + 1, punkty (-1, -1), (0, 1) i (1, 3) powinny być naniesione na płaszczyznę kartezjańską. Po narysowaniu linii, można łatwo zobaczyć, jak równanie zachowuje się w różnych punktach oraz jak przebiega w przestrzeni. To podejście nie tylko ułatwia graficzne przedstawienie równań, ale także pomaga w zrozumieniu ich właściwości.
- Przekształć równanie do postaci y = mx + b, aby ułatwić rysowanie wykresu.
- Wybierz różne wartości x, aby uzyskać odpowiadające wartości y.
- Nanieś punkty na wykres i połącz je linią prostą, aby zobaczyć graficzną reprezentację równania.
Analiza punktów przecięcia wykresów - znaczenie rozwiązań
Punkty przecięcia wykresów równań z dwiema niewiadomymi mają kluczowe znaczenie w kontekście rozwiązań układów równań. Kiedy dwa wykresy przecinają się w jednym punkcie, oznacza to, że układ równań ma jedno unikalne rozwiązanie. To rozwiązanie jest parą wartości (x, y), które spełniają oba równania jednocześnie. Z kolei, jeśli wykresy są równoległe, nie mają punktu przecięcia, co wskazuje na brak rozwiązań – układ jest sprzeczny. Natomiast, gdy wykresy pokrywają się, układ równań ma nieskończoną liczbę rozwiązań, co oznacza, że równania są liniowo zależne.
Przykłady z życia codziennego mogą pomóc w lepszym zrozumieniu znaczenia punktów przecięcia. Na przykład, rozważmy sytuację, w której dwie firmy ustalają ceny swoich produktów. Jeśli ich wykresy cenowe przecinają się, oznacza to, że obie firmy oferują ten sam produkt w tej samej cenie w danym momencie. W takim przypadku klienci mogą wybrać dowolną z firm. Z drugiej strony, jeśli jedna firma zawsze sprzedaje swój produkt drożej, ich wykresy nie będą się przecinać, co może prowadzić do utraty klientów. Analizując punkty przecięcia, możemy lepiej zrozumieć dynamikę rynku oraz podejmować bardziej świadome decyzje.
Wykorzystanie narzędzi cyfrowych do analizy równań liniowych
W dzisiejszych czasach, narzędzia cyfrowe odgrywają kluczową rolę w analizie równań z dwiema niewiadomymi. Programy takie jak GeoGebra czy Desmos umożliwiają użytkownikom łatwe rysowanie wykresów i wizualizację punktów przecięcia. Używając tych narzędzi, można szybko zobaczyć, jak zmiana wartości współczynników w równaniach wpływa na kształt i położenie wykresów, co jest niezwykle pomocne w zrozumieniu dynamiki układów równań.
Co więcej, analiza danych w połączeniu z technologią pozwala na modelowanie bardziej złożonych problemów, takich jak optymalizacja kosztów w biznesie czy analiza trendów rynkowych. Używając oprogramowania do analizy statystycznej, można zidentyfikować, które zmienne mają największy wpływ na wyniki, co może prowadzić do lepszego podejmowania decyzji. W przyszłości, integracja sztucznej inteligencji z tymi narzędziami może jeszcze bardziej uprościć proces analizy równań, oferując użytkownikom inteligentne sugestie dotyczące rozwiązań i strategii.

