Narzędzia TOC (Teoria Ograniczeń) w matematyce to innowacyjne metody, które mają na celu wspieranie procesu nauczania i uczenia się. Dzięki nim uczniowie mogą rozwijać umiejętności krytycznego myślenia, analizy oraz planowania. Główne narzędzia, takie jak Chmura, Gałąź i Drzewko Ambitnego Celu, oferują różnorodne podejścia do rozwiązywania problemów matematycznych, co pozwala na lepsze zrozumienie materiału oraz jego struktury.
W artykule przyjrzymy się, jak te narzędzia wpływają na rozwój myślenia krytycznego oraz jakie korzyści przynoszą w różnych kontekstach edukacyjnych. Zastosowanie narzędzi TOC może być kluczowe w motywowaniu uczniów do samodzielnej pracy oraz w poprawie komunikacji w klasie, co w rezultacie prowadzi do głębszego przyswajania wiedzy.
Kluczowe informacje:
- Narzędzia TOC wspierają rozwój umiejętności krytycznego myślenia i analizy.
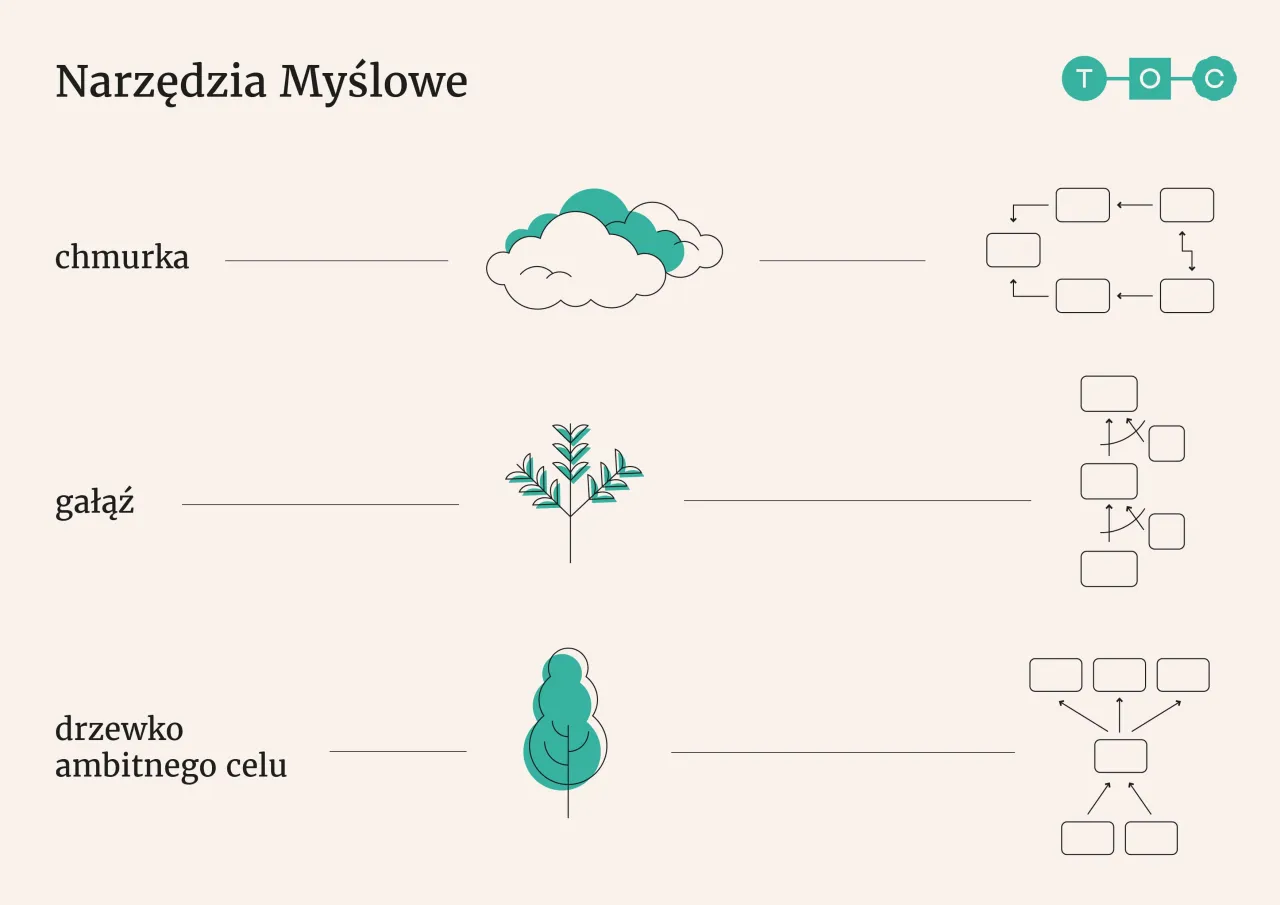
- Chmura umożliwia wizualizację problemów matematycznych, co ułatwia ich zrozumienie.
- Gałąź pozwala na analizę i planowanie zadań matematycznych, ujawniając związki przyczynowo-skutkowe.
- Drzewko Ambitnego Celu motywuje uczniów do wyznaczania i osiągania celów edukacyjnych.
- Narzędzia TOC są uniwersalne i mogą być stosowane w różnych poziomach edukacji, od przedszkola po szkołę wyższą.
Narzędzia TOC w matematyce i ich wpływ na nauczanie
Narzędzia TOC (Teoria Ograniczeń) w matematyce to innowacyjne metody, które mają na celu wspieranie procesu nauczania. Dzięki nim uczniowie mogą rozwijać umiejętności krytycznego myślenia, analizy i planowania. Te narzędzia są niezwykle ważne, ponieważ pomagają w zrozumieniu złożonych problemów matematycznych oraz w organizacji myśli. W kontekście edukacji matematycznej, narzędzia TOC oferują różnorodne podejścia, które mogą być stosowane na wszystkich poziomach nauczania.
Wprowadzenie narzędzi TOC do klasy może znacząco wpłynąć na efektywność nauczania. Umożliwiają one uczniom lepsze zrozumienie materiału, a także rozwijają ich umiejętności analityczne. Dzięki wizualizacji problemów matematycznych, uczniowie są w stanie identyfikować kluczowe elementy zadania, co prowadzi do głębszego przyswajania wiedzy i większej samodzielności w nauce.
Chmura jako narzędzie wizualizacji problemów matematycznych
Chmura to jedno z głównych narzędzi TOC, które służy do wizualizacji problemów matematycznych. Działa na zasadzie przedstawiania informacji w formie graficznej, co pozwala uczniom na lepsze zrozumienie struktury zadań. Dzięki Chmurze, uczniowie mogą zobaczyć różne warianty rozwiązań, co ułatwia im analizę i podejmowanie decyzji w kontekście rozwiązywania równań matematycznych.Przykłady zastosowania Chmury w klasie obejmują naukę równań liniowych, gdzie uczniowie mogą wizualizować różne rozwiązania i zrozumieć zależności między zmiennymi. Ponadto, Chmura może być używana do organizacji myśli podczas rozwiązywania bardziej złożonych problemów, co sprzyja twórczemu myśleniu i poprawia umiejętności logiczne.
- Wizualizacja równań liniowych, co pozwala na zrozumienie zależności między zmiennymi.
- Organizacja myśli podczas rozwiązywania problemów geometrycznych, co ułatwia analizę danych.
- Prezentacja różnych wariantów rozwiązań, co wspiera krytyczne myślenie uczniów.
Gałąź do analizy i planowania zadań matematycznych
Gałąź, znana również jako Logiczna Gałązka, jest jednym z kluczowych narzędzi TOC, które umożliwiają analizę i planowanie zadań matematycznych. Jej główną funkcją jest ujawnianie związków przyczynowo-skutkowych, co pozwala uczniom na lepsze zrozumienie kolejności działań. Dzięki Gałęzi, uczniowie mogą rozkładać złożone zadania na mniejsze kroki, co ułatwia im przewidywanie konsekwencji podejmowanych decyzji. Narzędzie to wspiera rozwój logicznego myślenia i umiejętności analitycznych, co jest niezwykle ważne w matematyce.Przykłady zastosowania Gałęzi w planowaniu lekcji obejmują różnorodne zadania matematyczne, takie jak rozwiązywanie równań, analiza funkcji czy zadania geometryczne. Nauczyciele mogą wykorzystać Gałąź do stworzenia struktury lekcji, która prowadzi uczniów przez poszczególne etapy rozwiązywania problemów. Na przykład, w trakcie nauki o równaniach kwadratowych, Gałąź może pomóc uczniom zrozumieć, jakie kroki należy podjąć, aby dojść do rozwiązania, co może znacznie zwiększyć ich pewność siebie i umiejętności.
| Typ zadania matematycznego | Opis zastosowania Gałęzi |
| Równania liniowe | Rozkładanie na etapy: identyfikacja zmiennych, przekształcanie równań. |
| Funkcje kwadratowe | Analiza postaci kanonicznej, wyznaczanie miejsc zerowych. |
| Zadania geometryczne | Rozkładanie na kroki: obliczanie pól, obwodów i objętości. |
Jak narzędzia TOC wspierają rozwój myślenia krytycznego
Rozwój myślenia krytycznego jest kluczowym elementem edukacji matematycznej, a narzędzia TOC (Teoria Ograniczeń) odgrywają w tym procesie istotną rolę. Dzięki zastosowaniu metod graficznych, takich jak Chmura czy Gałąź, uczniowie są w stanie analizować problemy z różnych perspektyw, co sprzyja lepszemu zrozumieniu materiału. Narzędzia te pozwalają na strukturalne podejście do zadań matematycznych, co ułatwia identyfikację kluczowych elementów i związków przyczynowo-skutkowych.
Wykorzystanie narzędzi TOC w klasie wspiera nie tylko logiczne myślenie, ale także umiejętności analityczne uczniów. Dzięki nim, uczniowie mogą samodzielnie podejmować decyzje i przewidywać konsekwencje swoich działań, co jest niezbędne w rozwiązywaniu problemów matematycznych. W rezultacie, narzędzia te przyczyniają się do zwiększenia samodzielności uczniów oraz ich zaangażowania w proces nauki.
Drzewko Ambitnego Celu w motywowaniu uczniów do nauki
Drzewko Ambitnego Celu to narzędzie TOC, które odgrywa kluczową rolę w motywowaniu uczniów do nauki poprzez wyznaczanie i osiąganie celów edukacyjnych. Jego główną zasadą jest wizualizacja procesu nauki, co pozwala uczniom śledzić postępy w realizacji zadań. Dzięki Drzewku, uczniowie mogą rozbijać złożone cele na mniejsze, łatwiejsze do osiągnięcia etapy, co zwiększa ich pewność siebie oraz zaangażowanie w proces nauczania.
W praktyce, Drzewko Ambitnego Celu zostało z powodzeniem wdrożone w wielu klasach. Na przykład, nauczyciele matematyki wykorzystują to narzędzie, aby pomóc uczniom w opanowaniu równań kwadratowych. Uczniowie zaczynają od podstawowych pojęć, takich jak dodawanie i odejmowanie, a następnie przechodzą do bardziej złożonych zadań, takich jak faktoryzacja. Takie podejście nie tylko ułatwia naukę, ale również motywuje uczniów do samodzielnego poszerzania wiedzy.
Przykłady zastosowania narzędzi TOC w różnych poziomach edukacji
Narzędzia TOC, takie jak Chmura, Gałąź oraz Drzewko Ambitnego Celu, znalazły zastosowanie na różnych poziomach edukacji, od przedszkola po szkołę średnią. W edukacji podstawowej, nauczyciele często wykorzystują Chmurę do wizualizacji prostych problemów matematycznych, co pomaga młodym uczniom w zrozumieniu podstawowych pojęć. Na przykład, podczas nauki dodawania i odejmowania, uczniowie mogą tworzyć Chmurę, aby zobaczyć powiązania między liczbami. W szkole średniej, Gałąź jest używana do analizy bardziej skomplikowanych zadań, takich jak równania kwadratowe, co pozwala uczniom zrozumieć, jak różne elementy wpływają na siebie nawzajem.
W kontekście edukacji wyższej, narzędzia TOC są wykorzystywane do rozwijania umiejętności analitycznych i krytycznego myślenia. Na przykład, w kursach matematyki stosowanej, studenci mogą korzystać z Drzewka Ambitnego Celu do wyznaczania celów projektów badawczych, co motywuje ich do systematycznego podejścia do nauki. Uczelnie wyższe, takie jak Uniwersytet Warszawski, wprowadziły programy, w których studenci wykorzystują metody TOC do analizy danych i rozwiązywania problemów w rzeczywistych sytuacjach.
| Poziom edukacji | Zastosowanie narzędzi TOC |
| Przedszkole | Wizualizacja prostych problemów matematycznych za pomocą Chmury |
| Szkoła podstawowa | Użycie Chmury do nauki dodawania i odejmowania |
| Szkoła średnia | Analiza zadań matematycznych przy użyciu Gałęzi |
| Szkoła wyższa | Wyznaczanie celów projektów badawczych z Drzewkiem Ambitnego Celu |
Integracja narzędzi TOC z technologią w edukacji matematycznej
W dzisiejszym świecie, gdzie technologia odgrywa kluczową rolę w edukacji, integracja narzędzi TOC z nowoczesnymi rozwiązaniami technologicznymi może znacząco zwiększyć efektywność nauczania matematyki. Na przykład, aplikacje mobilne i platformy edukacyjne mogą wykorzystywać metody TOC do stworzenia interaktywnych doświadczeń, które umożliwiają uczniom wizualizację problemów matematycznych w czasie rzeczywistym. Dzięki temu uczniowie mogą lepiej zrozumieć złożone koncepcje, a nauczyciele mają możliwość monitorowania postępów w nauce w sposób bardziej dynamiczny i angażujący.
W przyszłości, zastosowanie sztucznej inteligencji w połączeniu z narzędziami TOC może przynieść jeszcze większe korzyści. Systemy oparte na AI mogłyby dostosowywać materiały edukacyjne do indywidualnych potrzeb ucznia, identyfikując obszary wymagające wsparcia i proponując odpowiednie narzędzia TOC, takie jak Chmura czy Gałąź. Taka personalizacja nauki nie tylko zwiększyłaby motywację uczniów, ale także poprawiłaby ich wyniki w nauce, tworząc bardziej zindywidualizowane doświadczenie edukacyjne.

