Rozwiązywanie równań trygonometrycznych to kluczowa umiejętność w matematyce, która pozwala na przekształcanie skomplikowanych problemów w prostsze formy. Dzięki różnorodnym metodom, takim jak metoda podstawiania czy wykorzystanie tożsamości trygonometrycznych, można skutecznie znaleźć rozwiązania równań. W artykule przedstawimy podstawowe techniki oraz przykłady, które pomogą w zrozumieniu tego tematu.
Równania trygonometryczne mogą wydawać się trudne, ale z odpowiednimi narzędziami i metodami, ich rozwiązywanie staje się znacznie prostsze. Kluczowe jest zrozumienie podstawowych pojęć oraz umiejętność stosowania różnych strategii, co umożliwia efektywne podejście do problemów matematycznych.
Najważniejsze informacje:
- Równania trygonometryczne można uprościć do postaci elementarnych, co ułatwia ich rozwiązanie.
- Metoda podstawiania polega na wprowadzeniu zmiennej pomocniczej, co przekształca równanie w algebraiczne.
- Tożsamości trygonometryczne, takie jak $$\sin^2{x} + \cos^2{x} = 1$$, są kluczowe w procesie rozwiązywania równań.
- Ważne jest zrozumienie dziedziny funkcji trygonometrycznych, aby uniknąć błędów w rozwiązaniach.
- Graficzne podejście do równań trygonometrycznych może pomóc w wizualizacji i identyfikacji rozwiązań.
Rozwiązywanie równań trygonometrycznych - podstawowe metody i techniki
Rozwiązywanie równań trygonometrycznych to proces, który polega na przekształcaniu skomplikowanych równań w prostsze formy, które można łatwiej rozwiązać. W tym kontekście kluczowe jest zrozumienie podstawowych pojęć związanych z równaniami trygonometrycznymi oraz metod, które można zastosować w ich rozwiązywaniu. Równania te często zawierają funkcje trygonometryczne, takie jak sinus, cosinus czy tangens, które wymagają specjalnych technik do efektywnego rozwiązania.
Wśród podstawowych metod rozwiązywania równań trygonometrycznych znajdują się różne podejścia, takie jak algebraiczne manipulacje oraz wykorzystanie funkcji odwrotnych. Te techniki pozwalają na uproszczenie równań, co ułatwia znalezienie ich rozwiązań. Kluczowe jest również umiejętne posługiwanie się tożsamościami trygonometrycznymi, które mogą być przydatne w wielu sytuacjach. W kolejnych sekcjach artykułu zostaną przedstawione szczegółowe metody oraz przykłady, które pomogą w zrozumieniu tego zagadnienia.
Zrozumienie równań trygonometrycznych - kluczowe pojęcia
Równania trygonometryczne to wyrażenia matematyczne, w których występują funkcje trygonometryczne. Typowe równania trygonometryczne mogą mieć różne formy, na przykład $$\sin{x} = a$$, $$\cos{x} = b$$ lub $$\tan{x} = c$$, gdzie a, b, c to stałe. Równania te mogą mieć jedno, kilka lub nawet nieskończoną liczbę rozwiązań, w zależności od ich struktury. Zrozumienie charakterystyki tych równań jest kluczowe dla skutecznego ich rozwiązywania.
Podstawowe metody rozwiązywania równań trygonometrycznych
Rozwiązywanie równań trygonometrycznych wymaga znajomości kilku podstawowych technik. Jedną z najczęściej stosowanych metod jest manipulacja algebraiczna, która polega na przekształcaniu równań w celu uproszczenia ich formy. Na przykład, równanie $$\sin^2{x} + \cos^2{x} = 1$$ można przekształcić, aby wyrazić jedną funkcję w zależności od drugiej, co ułatwia dalsze analizy. Warto również zwrócić uwagę na funkcje odwrotne, które mogą być użyte do rozwiązania równań, takich jak $$\sin^{-1}(x)$$ czy $$\cos^{-1}(x)$$, co pozwala na określenie wartości kątów odpowiadających danym wartościom funkcji trygonometrycznych.
Innym przykładem jest równanie $$\tan{x} = 1$$, które można rozwiązać, korzystając z funkcji odwrotnej tangensa, co prowadzi do $$x = \frac{\pi}{4} + k\pi$$, gdzie $$k$$ jest liczbą całkowitą. Takie podejście pozwala na szybkie wyznaczenie kątów, które spełniają dane równanie. Kluczowe jest, aby podczas rozwiązywania równań trygonometrycznych umiejętnie łączyć te metody, co znacząco ułatwia proces znajdowania rozwiązań.
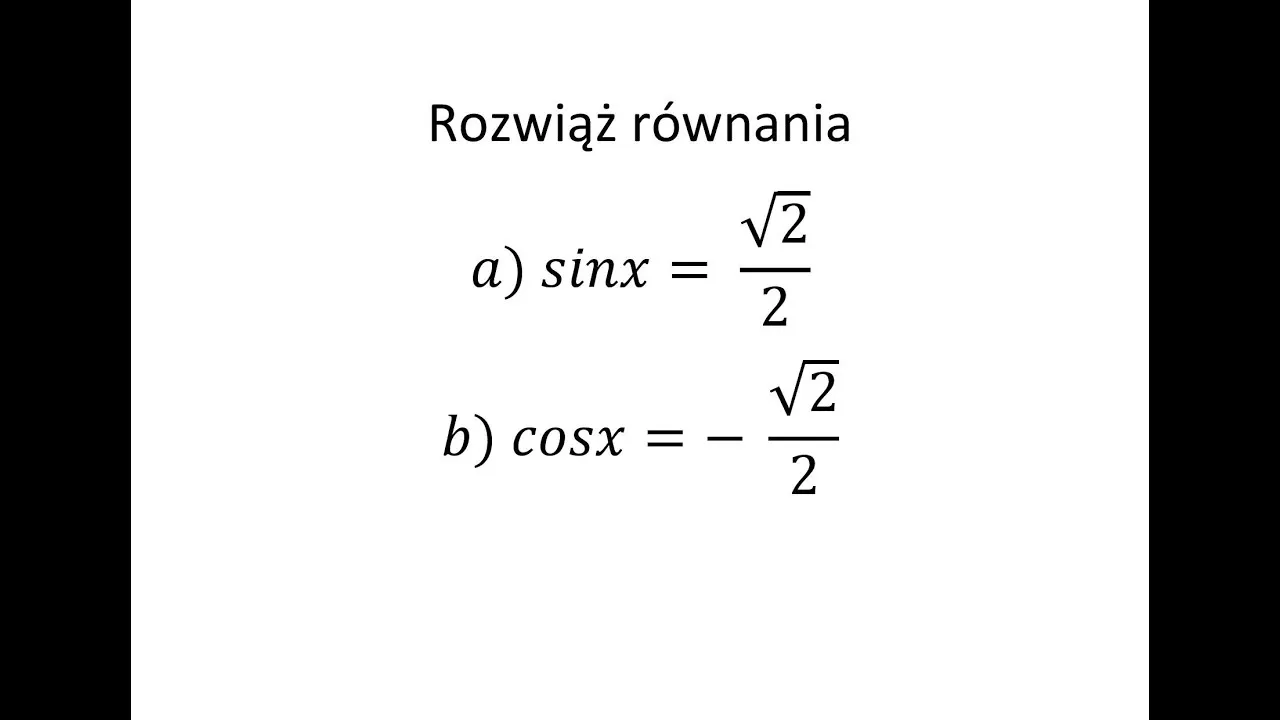
Użycie tożsamości trygonometrycznych w rozwiązywaniu równań
Tożsamości trygonometryczne odgrywają istotną rolę w procesie rozwiązywania równań trygonometrycznych. Dzięki nim można przekształcać skomplikowane równania w prostsze formy, co ułatwia ich rozwiązanie. Na przykład, tożsamość $$\sin^2{x} + \cos^2{x} = 1$$ pozwala na zamianę funkcji sinus na funkcję cosinus i odwrotnie, co jest niezwykle przydatne w sytuacjach, gdy równania zawierają zarówno sinusy, jak i cosinusy. W praktyce, umiejętne stosowanie tych tożsamości pozwala na uproszczenie równań, co przyspiesza proces ich rozwiązywania.
Innym przykładem jest wykorzystanie wzorów na sumę kątów, takich jak $$\sin(a + b) = \sin{a}\cos{b} + \cos{a}\sin{b}$$, które mogą być zastosowane do przekształcania równań. Dzięki tym tożsamościom można łatwiej zidentyfikować rozwiązania równań, które na pierwszy rzut oka mogą wydawać się trudne do rozwiązania. W kolejnych częściach artykułu zaprezentujemy konkretne przykłady zastosowania tożsamości w praktyce.
| Tożsamość | Opis |
| $$\sin^2{x} + \cos^2{x} = 1$$ | Podstawowa tożsamość trygonometryczna, używana do przekształcania równań. |
| $$\tan{x} = \frac{\sin{x}}{\cos{x}}$$ | Definicja tangensa w zależności od sinusa i cosinusa. |
| $$\sin(a + b)$$ | Wzór na sumę kątów, przydatny w złożonych równaniach. |
Kluczowe tożsamości trygonometryczne - jak je stosować
Tożsamości trygonometryczne są fundamentalnymi narzędziami w rozwiązywaniu równań trygonometrycznych. Najbardziej znaną z nich jest tożsamość Pitagorejska, która mówi, że $$\sin^2{x} + \cos^2{x} = 1$$. Umożliwia ona przekształcanie równań, co pozwala na uproszczenie skomplikowanych wyrażeń. Inne ważne tożsamości to wzory na sumę kątów, takie jak $$\sin(a + b) = \sin{a}\cos{b} + \cos{a}\sin{b}$$ oraz $$\cos(a + b) = \cos{a}\cos{b} - \sin{a}\sin{b}$$, które pomagają w rozwiązywaniu równań, w których występują sumy kątów.
Warto także zwrócić uwagę na tożsamości odwrotne, takie jak $$\sin^{-1}(x)$$, $$\cos^{-1}(x)$$ i $$\tan^{-1}(x)$$, które są użyteczne w kontekście znajdowania kątów odpowiadających wartościom funkcji trygonometrycznych. Dzięki tym tożsamościom, można zamieniać różne funkcje trygonometryczne, co znacznie ułatwia proces rozwiązywania równań. Zrozumienie i umiejętne stosowanie tych tożsamości jest kluczowe dla każdego, kto chce skutecznie rozwiązywać równania trygonometryczne.
Przykłady zastosowania tożsamości w równaniach
W praktyce tożsamości trygonometryczne są używane do przekształcania równań w celu ich uproszczenia. Na przykład, równanie $$\sin^2{x} = 1 - \cos^2{x}$$ można przekształcić przy użyciu tożsamości Pitagorejskiej, co pozwala na łatwiejsze rozwiązanie. Innym przykładem jest równanie $$\tan{x} = \frac{\sin{x}}{\cos{x}}$$, które można wykorzystać do przekształcenia równania do formy $$\sin{x} = k \cdot \cos{x}$$, gdzie $$k$$ jest stałą. Takie podejście pozwala na uproszczenie równań i ułatwia znalezienie ich rozwiązań.
W przypadku bardziej złożonych równań, takich jak $$\sin(2x) = 2\sin{x}\cos{x}$$, stosowanie wzoru na podwójny kąt może być kluczowe dla uproszczenia równania. Dzięki tożsamościom trygonometrycznym, można zredukować złożoność równań, co prowadzi do szybszego i bardziej efektywnego rozwiązywania problemów. Umiejętne korzystanie z tych tożsamości jest niezbędne dla każdego, kto chce stać się biegły w rozwiązywaniu równań z funkcjami trygonometrycznymi.
Jak skutecznie wprowadzać zmienne pomocnicze
Wprowadzenie zmiennych pomocniczych w równaniach trygonometrycznych jest kluczową strategią, która może znacząco uprościć proces rozwiązywania. Stosowanie zmiennych pomocniczych, takich jak $$t = \sin{x}$$ lub $$t = \cos{x}$$, pozwala na przekształcenie równań trygonometrycznych w równania algebraiczne, które są łatwiejsze do analizy. Dzięki temu można zredukować złożoność równań i skupić się na ich rozwiązaniu w bardziej znajomej formie. Wprowadzenie zmiennej pomocniczej nie tylko ułatwia obliczenia, ale również pozwala na lepsze zrozumienie struktury równania.
Warto również pamiętać, że zmienne pomocnicze powinny być wprowadzane w sposób przemyślany, aby uniknąć wprowadzenia dodatkowych komplikacji. Kluczowe jest, aby po rozwiązaniu równania z nową zmienną, wrócić do oryginalnych funkcji trygonometrycznych, aby uzyskać pełne rozwiązanie. Takie podejście jest szczególnie pomocne w przypadku równań kwadratowych, gdzie można z łatwością zastosować znane metody rozwiązywania, takie jak faktoryzacja czy wzory kwadratowe.
Przykłady równań z zastosowaniem metody podstawiania
Przykładem zastosowania metody podstawiania może być równanie $$2\sin^2{x} - 3\sin{x} + 1 = 0$$. W tym przypadku można wprowadzić zmienną pomocniczą $$t = \sin{x}$$, co przekształca równanie w postać kwadratową $$2t^2 - 3t + 1 = 0$$. Po rozwiązaniu tego równania kwadratowego, uzyskuje się wartości zmiennej pomocniczej, które następnie należy przekształcić z powrotem na funkcje trygonometryczne. Innym przykładem może być równanie $$\cos^2{x} - \sin{x} = 0$$, gdzie można zastosować podstawienie $$t = \sin{x}$$, co prowadzi do $$1 - t^2 - t = 0$$. Takie przekształcenia umożliwiają łatwiejsze znalezienie rozwiązań i są powszechnie stosowane w praktyce.
Ograniczenia funkcji trygonometrycznych - co musisz wiedzieć
Funkcje trygonometryczne, takie jak sinus, cosinus i tangens, mają swoje ograniczenia, które wpływają na rozwiązania równań trygonometrycznych. Na przykład, funkcja sinus i cosinus mają wartości ograniczone w przedziale od -1 do 1, co oznacza, że równania takie jak $$\sin{x} = a$$ i $$\cos{x} = a$$ mają rozwiązania tylko wtedy, gdy $$a$$ mieści się w tym zakresie. Natomiast funkcja tangens nie ma takich ograniczeń, ale jej dziedzina jest ograniczona, ponieważ $$\tan{x}$$ jest niezdefiniowane dla kątów, gdzie $$x = \frac{\pi}{2} + k\pi$$, gdzie $$k$$ jest liczbą całkowitą. Zrozumienie tych ograniczeń jest kluczowe, aby poprawnie interpretować wyniki równań trygonometrycznych.
Jak sprawdzać rozwiązania - unikanie fałszywych wyników
Weryfikacja rozwiązań równań trygonometrycznych jest niezbędna, aby uniknąć fałszywych wyników. Po znalezieniu potencjalnych rozwiązań, ważne jest, aby zastąpić je z powrotem w oryginalnym równaniu, aby upewnić się, że spełniają one wszystkie warunki. Często, zwłaszcza przy operacjach takich jak podnoszenie do kwadratu, mogą pojawić się dodatkowe rozwiązania, które nie są rzeczywistymi rozwiązaniami równania. Dlatego warto skorzystać z wykresów funkcji, aby wizualizować rozwiązania i sprawdzić, czy są one zgodne z oczekiwaniami. Regularne stosowanie takich technik weryfikacyjnych pomoże w zwiększeniu dokładności i pewności w rozwiązywaniu równań trygonometrycznych.
Jak wykorzystać równania trygonometryczne w praktycznych zastosowaniach
Równania trygonometryczne znajdują zastosowanie nie tylko w matematyce teoretycznej, ale również w wielu dziedzinach życia codziennego oraz w różnych branżach. Na przykład, w inżynierii mechanicznej i budowlanej, znajomość funkcji trygonometrycznych jest niezbędna do obliczania kątów, sił oraz momentów, co ma kluczowe znaczenie dla projektowania stabilnych konstrukcji. W praktyce, inżynierowie często wykorzystują równania trygonometryczne do analizy ruchu, co pozwala na dokładne przewidywanie trajektorii obiektów.
Dodatkowo, w dziedzinie technologii i informatyki, algorytmy oparte na funkcjach trygonometrycznych są wykorzystywane w grafice komputerowej, symulacjach fizycznych oraz w tworzeniu gier. Dzięki tym algorytmom można realistycznie odwzorować ruchy obiektów w wirtualnym świecie, co znacząco podnosi jakość wizualizacji. Zrozumienie, jak stosować równania trygonometryczne w takich kontekstach, otwiera nowe możliwości dla studentów i profesjonalistów, którzy chcą rozwijać swoje umiejętności w praktycznych zastosowaniach matematyki.
