W artykule przedstawimy praktyczne zastosowania wzorów logarytmicznych, które pomogą w zrozumieniu, jak dzielić logarytmy w różnych kontekstach matematycznych. Omówimy także różnice między logarytmem naturalnym a dziesiętnym, co jest istotne dla poprawnych obliczeń w różnych dziedzinach nauki.
Najważniejsze informacje:
- Nie ma bezpośredniego dzielenia logarytmów; zamiast tego używa się wzorów.
- Wzór na różnicę logarytmów: log_a b - log_a c = log_a (b/c).
- Logarytmy dziesiętne i naturalne mają różne zastosowania w matematyce i naukach przyrodniczych.
- Przykłady zadań ilustrujących dzielenie logarytmów pomagają w zrozumieniu praktycznego zastosowania wzorów.
- Zrozumienie podstawowych właściwości logarytmów jest kluczowe dla ich efektywnego wykorzystania.
Zrozumienie podstawowych właściwości logarytmów dla dzielenia
Aby zrozumieć, jak dzielić logarytmy, kluczowe jest poznanie podstawowych właściwości logarytmów. Logarytmy to potężne narzędzie w matematyce, które pozwala na przekształcanie skomplikowanych wyrażeń w prostsze formy. W kontekście dzielenia logarytmów, istotne jest, że nie wykonujemy bezpośredniego dzielenia jednego logarytmu przez drugi. Zamiast tego, wykorzystujemy właściwości logarytmów, które umożliwiają nam manipulację tymi wyrażeniami.
Główną zasadą, którą należy zrozumieć, jest wzór na różnicę logarytmów. Mówi on, że różnica logarytmów o tej samej podstawie można zapisać jako logarytm ilorazu ich argumentów. Ta zasada jest fundamentalna dla wszelkich obliczeń związanych z dzieleniem logarytmów. Dzięki temu możemy upraszczać złożone wyrażenia, co jest niezwykle przydatne w różnych dziedzinach matematyki oraz nauk przyrodniczych.
Jakie są podstawowe wzory logarytmiczne do dzielenia?
Podstawowym wzorem, który należy znać w kontekście dzielenia logarytmów, jest wzór na różnicę logarytmów. Wyrażenie to można zapisać jako: log_a b - log_a c = log_a (b/c). Oznacza to, że jeśli mamy dwa logarytmy o tej samej podstawie, możemy je od siebie odjąć, a wynik będzie równy logarytmowi ilorazu ich argumentów. Przykład tego wzoru można zobaczyć w przypadku logarytmów o podstawie 3: log_3 18 - log_3 2 = log_3 (18/2) = log_3 9 = 2.
Warto również pamiętać, że logarytm dziesiętny (oznaczany jako log) oraz logarytm naturalny (oznaczany jako ln) mają różne zastosowania, ale zasady dotyczące ich dzielenia pozostają takie same. Zrozumienie tych wzorów jest kluczowe dla dalszego rozwiązywania zadań związanych z logarytmami i ich praktycznym zastosowaniem w matematyce oraz naukach przyrodniczych.
Dlaczego dzielenie logarytmów jest ważne w matematyce?
Dzielenie logarytmów odgrywa kluczową rolę w matematyce, ponieważ pozwala na uproszczenie skomplikowanych równań i wyrażeń. Dzięki logarytmom możemy łatwiej rozwiązywać problemy, które w przeciwnym razie byłyby zbyt trudne do obliczenia. Logarytmy są szczególnie przydatne w kontekście równań wykładniczych, gdzie ich właściwości umożliwiają przekształcanie równań do bardziej przejrzystych postaci, co ułatwia ich rozwiązanie.
W praktyce, umiejętność dzielenia logarytmów jest niezbędna w wielu dziedzinach, takich jak chemia, fizyka czy ekonomia. Na przykład, w chemii często używa się logarytmów do obliczania pH roztworów, gdzie znajomość wzorów logarytmicznych pozwala na szybkie i efektywne przekształcanie danych. W ten sposób, dzielenie logarytmów staje się nie tylko teoretycznym narzędziem, ale także praktycznym sposobem na rozwiązywanie rzeczywistych problemów.
Praktyczne zastosowanie wzorów logarytmicznych w dzieleniu
W praktyce, jak dzielić logarytmy można zrozumieć poprzez zastosowanie odpowiednich wzorów w różnych sytuacjach. Na przykład, w finansach, logarytmy są używane do obliczania stóp zwrotu z inwestycji. W takim przypadku, umiejętność manipulowania logarytmami pozwala na lepsze zrozumienie zysków i strat. Warto zauważyć, że stosując wzory logarytmiczne, można znacznie uprościć obliczenia, co jest kluczowe w analizie danych.
Innym przykładem zastosowania logarytmów jest analiza danych w naukach przyrodniczych. Na przykład, w biologii, logarytmy mogą być używane do obliczania wzrostu populacji organizmów, gdzie zmiany w liczbie osobników mogą być modelowane za pomocą równań logarytmicznych. Dzięki temu, naukowcy mogą przewidywać przyszłe zmiany w populacji, co jest niezwykle istotne dla zachowania bioróżnorodności i ochrony gatunków.
Jak przekształcać logarytmy przy użyciu wzorów?
Przekształcanie logarytmów przy użyciu wzorów to kluczowa umiejętność, która pozwala na uproszczenie skomplikowanych wyrażeń matematycznych. Istnieje kilka technik, które można zastosować, aby manipulować logarytmicznymi wyrażeniami. Na przykład, wykorzystując wzór na różnicę logarytmów, możemy łatwo przekształcić log_a b - log_a c w log_a (b/c). Tego typu przekształcenia są niezwykle przydatne w rozwiązywaniu równań i ułatwiają obliczenia.
Innym sposobem na przekształcanie logarytmów jest zastosowanie wzoru na iloczyn logarytmów. Zgodnie z tym wzorem, log_a (b \cdot c) = log_a b + log_a c. Dzięki temu, możemy zamienić iloczyn dwóch liczb na sumę ich logarytmów, co często upraszcza obliczenia. Przykładowo, zamiast obliczać log_2 (8 \cdot 4), możemy zastosować wzór i obliczyć to jako log_2 8 + log_2 4, co daje 3 + 2 = 5.
Przykłady zadań ilustrujących dzielenie logarytmów
W praktyce, umiejętność dzielenia logarytmów jest niezbędna w wielu dziedzinach. Na przykład, w finansach, aby obliczyć stopę zwrotu z inwestycji, możemy użyć logarytmów. Jeśli chcemy obliczyć log_2 32 - log_2 8, stosując wzór na różnicę logarytmów, otrzymujemy log_2 (32/8) = log_2 4 = 2. Dzięki temu, możemy szybko i efektywnie uzyskać potrzebne informacje o stopie zwrotu.
Innym przykładem może być zastosowanie logarytmów w naukach przyrodniczych. Na przykład, w chemii, obliczając pH roztworu, często korzystamy z logarytmu dziesiętnego. Jeśli mamy pH równe 3, to możemy zapisać to jako -log_{10} [H^+], co oznacza, że stężenie jonów wodoru wynosi [H^+] = 10^{-3}
Czytaj więcej: Jak obliczyć pole trójkąta równoramiennego? Proste metody i wzory
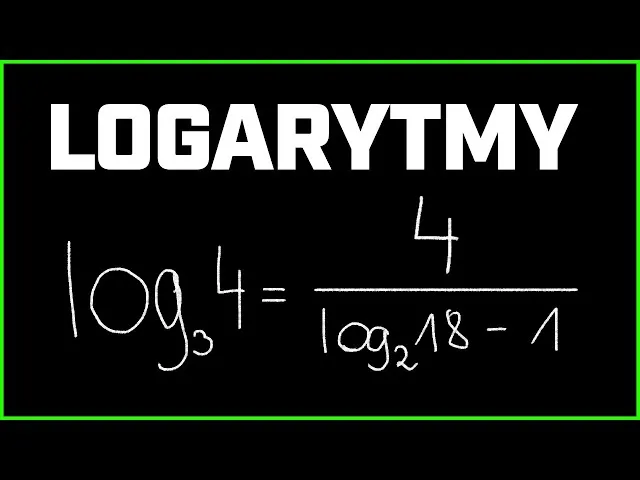
Różnice między logarytmem naturalnym a dziesiętnym
Logarytmy naturalne i dziesiętne różnią się przede wszystkim podstawą, co ma istotne znaczenie w zastosowaniach matematycznych. Logarytm naturalny, oznaczany jako ln, ma podstawę e (około 2,718), podczas gdy logarytm dziesiętny, oznaczany jako log, ma podstawę 10. Ta różnica wpływa na sposób, w jaki obliczamy wartości logarytmiczne oraz na kontekst, w jakim są one używane. Logarytmy naturalne są często stosowane w matematyce i naukach przyrodniczych, zwłaszcza w analizie ciągów i równań różniczkowych, natomiast logarytmy dziesiętne są powszechnie używane w praktycznych zastosowaniach, takich jak obliczenia pH w chemii.
W przypadku dzielenia logarytmów, wybór podstawy może wpłynąć na wyniki obliczeń. Na przykład, dzieląc logarytmy o różnych podstawach, musimy pamiętać o przekształceniu ich na wspólną podstawę, aby uzyskać poprawne wyniki. W praktyce oznacza to, że używając logarytmu naturalnego dla obliczeń finansowych, które zazwyczaj preferują logarytmy dziesiętne, powinniśmy być ostrożni. Właściwe zrozumienie różnic między tymi dwoma typami logarytmów jest kluczowe dla efektywnego rozwiązywania problemów matematycznych oraz naukowych.
Jak różne podstawy logarytmów wpływają na obliczenia?
Podstawa logarytmu ma znaczący wpływ na wyniki obliczeń. Kiedy używamy logarytmów w różnych dziedzinach, takich jak finanse czy chemia, musimy być świadomi, że różne podstawy mogą prowadzić do różnych wartości logarytmicznych. Na przykład, obliczając log_10 1000, otrzymujemy 3, ponieważ 10 do potęgi 3 równa się 1000. Jednak, jeśli obliczymy ln 1000, wynik będzie zupełnie inny, ponieważ podstawą jest e.
W praktyce oznacza to, że przy dzieleniu logarytmów musimy dostosować podstawy, aby uzyskać spójne wyniki. Na przykład, aby podzielić log_{10} 100 przez ln 100, musimy najpierw przekształcić jeden z logarytmów na podstawę drugiego, co wymaga znajomości wzorów konwersji logarytmów. Ta umiejętność jest niezbędna, aby uniknąć błędów w obliczeniach i uzyskać dokładne wyniki w zastosowaniach praktycznych.
Kiedy stosować logarytmy naturalne w dzieleniu?
Logarytmy naturalne, oznaczane jako ln, są szczególnie przydatne w kontekście dzielenia, gdy zajmujemy się problemami związanymi z procesami ciągłymi. Na przykład, w naukach przyrodniczych, takich jak biologia czy chemia, logarytmy naturalne często stosuje się do modelowania wzrostu populacji lub reakcji chemicznych. Zastosowanie logarytmów naturalnych w tych dziedzinach umożliwia lepsze zrozumienie dynamiki procesów, które zachodzą w czasie. Gdy potrzebujemy obliczyć iloraz logarytmów w kontekście tych procesów, naturalne logarytmy są bardziej odpowiednie niż logarytmy dziesiętne.Innym kontekstem, w którym logarytmy naturalne są preferowane, jest analiza danych w statystyce. W przypadku, gdy dane są rozkładane wykładniczo, użycie logarytmu naturalnego ułatwia obliczenia i interpretację wyników. Na przykład, w analizie regresji, logarytmy naturalne mogą pomóc w przekształceniu nieliniowych zależności w liniowe, co znacznie ułatwia dalsze obliczenia. W takich sytuacjach, wybór logarytmu naturalnego jako podstawy dla dzielenia jest kluczowy dla uzyskania dokładnych i użytecznych wyników.
Praktyczne zastosowania logarytmów w analizie danych i AI
W miarę jak technologia i analiza danych stają się coraz bardziej zaawansowane, logarytmy naturalne i dziesiętne zyskują na znaczeniu w kontekście sztucznej inteligencji i uczenia maszynowego. W aplikacjach AI, logarytmy są często wykorzystywane do normalizacji danych, co pozwala na lepsze modelowanie i przewidywanie wyników. Na przykład, w przypadku danych o dużej rozpiętości, takich jak wyniki finansowe lub pomiary biologiczne, przekształcenie tych danych za pomocą logarytmów może pomóc w uzyskaniu bardziej stabilnych i przewidywalnych modeli.Co więcej, logarytmy są kluczowe w algorytmach optymalizacji, takich jak te używane w sieciach neuronowych. Przy obliczaniu funkcji straty, logarytmy naturalne mogą być wykorzystywane do oceny różnicy między przewidywaniami modelu a rzeczywistymi wynikami. Takie podejście nie tylko poprawia dokładność, ale także przyspiesza proces uczenia się modelu. W przyszłości, z coraz większym naciskiem na dane i ich analizę, umiejętność efektywnego stosowania logarytmów w kontekście AI stanie się niezbędna dla specjalistów w dziedzinie danych.

