W tym artykule przyjrzymy się podstawowym zasadom mnożenia logarytmów, kluczowym wzorom oraz najczęstszym błędom, które mogą pojawić się podczas ich stosowania. Zrozumienie tych zasad pozwoli na efektywne przekształcanie i uproszczenie wyrażeń logarytmicznych, co jest niezbędne w wielu dziedzinach matematyki.
Najważniejsze informacje:
- Logarytm iloczynu dwóch liczb można przedstawić jako sumę logarytmów tych liczb.
- Wzór: log_a(b * c) = log_a(b) + log_a(c) jest kluczowy dla uproszczenia wyrażeń.
- Mnożenie logarytmu przez liczbę można przekształcić w wykładnik: c * log_a(b) = log_a(b^c).
- Istnieją reguły dla mnożenia logarytmów o różnych podstawach, które należy znać.
- Unikaj typowych błędów, takich jak mylenie wzorów dla iloczynu i ilorazu.
Jak mnożyć logarytmy: zasady i podstawowe właściwości
Mnożenie logarytmów jest kluczowym elementem w matematyce, który pozwala na przekształcanie wyrażeń logarytmicznych. Warto zrozumieć, że nie chodzi tutaj o bezpośrednie mnożenie logarytmów jako liczb, lecz o zastosowanie ich właściwości do manipulacji argumentami. Istotne jest, aby znać podstawowe zasady, które rządzą tym procesem, ponieważ umożliwiają one uproszczenie złożonych wyrażeń matematycznych.
W kontekście logarytmów, mnożenie odnosi się do operacji, które pozwalają na łączenie logarytmów w sposób, który ułatwia ich dalsze przetwarzanie. Kluczowym wzorem jest to, że logarytm iloczynu dwóch liczb można przedstawić jako sumę logarytmów tych liczb przy tej samej podstawie. Zrozumienie tych zasad jest niezbędne dla każdego, kto chce efektywnie pracować z logarytmami w matematyce.
Zrozumienie podstawowych zasad mnożenia logarytmów dla uproszczenia
Podstawowe zasady mnożenia logarytmów opierają się na kilku kluczowych definicjach i regułach. Mnożenie logarytmów polega na wykorzystaniu wzorów, które pozwalają na przekształcanie wyrażeń w bardziej zrozumiałą formę. Na przykład, logarytm iloczynu można zredukować do sumy logarytmów poszczególnych składników, co jest niezwykle przydatne w procesie rozwiązywania równań.
Warto również zwrócić uwagę na to, że zasady te są fundamentalne dla uproszczenia skomplikowanych wyrażeń matematycznych. Mnożenie logarytmów nie tylko ułatwia obliczenia, ale także pozwala na lepsze zrozumienie relacji między różnymi wartościami. Dzięki tym zasadom, można skuteczniej analizować i rozwiązywać problemy matematyczne związane z logarytmami.
Kluczowe wzory logarytmiczne do efektywnego mnożenia
W matematyce istnieje kilka kluczowych wzorów, które są niezbędne do efektywnego mnożenia logarytmów. Najważniejszym z nich jest wzór na logarytm iloczynu, który brzmi: log_a(b \cdot c) = log_a(b) + log_a(c). Oznacza to, że logarytm z iloczynu dwóch liczb można przedstawić jako sumę logarytmów tych liczb. Ten wzór jest fundamentalny, ponieważ pozwala na uproszczenie złożonych wyrażeń matematycznych.
Kolejnym istotnym wzorem jest wzór na mnożenie logarytmu przez liczbę: c \cdot log_a(b) = log_a(b^c). Dzięki temu wzorowi, liczba stojąca przed logarytmem może być przeniesiona jako wykładnik argumentu logarytmu. Na przykład, jeśli mamy 3 \cdot log_5(25), możemy to przekształcić w log_5(25^3), co znacząco upraszcza obliczenia. Te podstawowe wzory stanowią fundament, na którym opiera się dalsze zrozumienie logarytmów.
Krok po kroku: mnożenie logarytmów z różnymi podstawami
Mnożenie logarytmów z różnymi podstawami może być nieco bardziej skomplikowane, ale z odpowiednimi zasadami można to wykonać bez problemu. Aby mnożyć logarytmy o różnych podstawach, najpierw musimy przekształcić je do wspólnej podstawy. Można to zrobić za pomocą wzoru: log_a(b) = log_c(b) / log_c(a), gdzie c jest nową podstawą, którą wybieramy. Na przykład, aby pomnożyć log_2(3) i log_3(4), możemy użyć podstawy 10 lub e (naturalny logarytm).
W naszym przypadku, przekształcamy logarytmy do wspólnej podstawy, co pozwala nam na ich łatwe mnożenie. Po przekształceniu, możemy połączyć je w jeden logarytm, co ułatwia obliczenia. Na przykład, po przekształceniu uzyskujemy: log_2(3) = log(3) / log(2) oraz log_3(4) = log(4) / log(3). Następnie, mnożymy te wartości, co daje nam log_2(4), co można obliczyć jako 2. Taki proces umożliwia efektywne wykorzystanie logarytmów w różnych kontekstach matematycznych.
| Podstawa | Logarytm | Przykład |
| 2 | log_2(8) | 3 (ponieważ 2^3 = 8) |
| 3 | log_3(27) | 3 (ponieważ 3^3 = 27) |
| 10 | log_10(100) | 2 (ponieważ 10^2 = 100) |
Przykłady zastosowania mnożenia logarytmów w zadaniach
Mnożenie logarytmów znajduje zastosowanie w wielu zadaniach matematycznych, które wymagają uproszczenia złożonych wyrażeń. Na przykład, w zadaniach dotyczących obliczeń finansowych, logarytmy mogą być używane do modelowania wzrostu kapitału. Przy pomocy wzorów logarytmicznych, można obliczyć czas potrzebny na osiągnięcie określonego zysku, co jest szczególnie przydatne w analizach inwestycyjnych.
Innym przykładem może być rozwiązywanie równań, gdzie logarytmy pojawiają się w kontekście funkcji wykładniczych. Używając reguł mnożenia logarytmów, można skutecznie uprościć równania, co prowadzi do szybszych wyników. Na przykład, w równaniu log_a(x) + log_a(y) = log_a(xy), możemy łatwo obliczyć wartość x i y, co jest nieocenione w praktycznych zastosowaniach matematycznych.
Typowe błędy przy mnożeniu logarytmów i jak ich unikać
Podczas pracy z logarytmami, szczególnie przy ich mnożeniu, mogą wystąpić różne typowe błędy, które mogą prowadzić do niepoprawnych wyników. Jednym z najczęstszych błędów jest mylenie wzorów dla iloczynu i ilorazu. Na przykład, niektórzy uczniowie mogą pomylić log_a(b \cdot c) z log_a(b) + log_a(c), co jest błędne w kontekście ilorazu. Ważne jest, aby zawsze upewnić się, że rozumiemy, które wzory stosować w danej sytuacji.
Kolejnym powszechnym błędem jest stosowanie wzorów bez sprawdzenia, czy logarytmy mają tę samą podstawę. Mnożenie logarytmów o różnych podstawach wymaga przekształcenia ich do wspólnej podstawy, co jest kluczowe dla uzyskania poprawnych wyników. Aby uniknąć tych pułapek, warto regularnie ćwiczyć różne zadania związane z logarytmami i korzystać z wizualizacji, które pomogą w zrozumieniu zasad ich działania.
Najczęstsze pułapki w stosowaniu wzorów logarytmicznych
W trakcie nauki o logarytmach, istnieje wiele pułapek, które mogą wprowadzić w błąd. Na przykład, niektórzy uczniowie mogą sądzić, że log_a(b) \cdot log_a(c) = log_a(b \cdot c), co jest błędne. W rzeczywistości, mnożenie logarytmów nie prowadzi do prostego logarytmu iloczynu. Inna pułapka to błędne stosowanie wzoru dla logarytmów o różnych podstawach, co może prowadzić do niepoprawnych obliczeń. Kluczowe jest, aby zrozumieć, że każda sytuacja wymaga analizy, aby zastosować odpowiednie zasady i uniknąć błędów.
Czytaj więcej: Wykrzyknik w matematyce: Zrozumienie symbolu silni i jego zastosowań
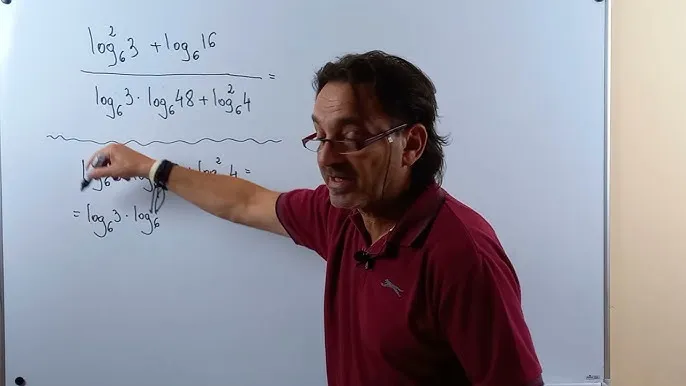
Jak poprawnie stosować zasady logarytmów w praktyce
Aby skutecznie stosować zasady logarytmów w praktyce, warto przestrzegać kilku kluczowych strategii. Po pierwsze, zawsze upewniaj się, że masz do czynienia z logarytmami o tej samej podstawie, zanim zaczniesz je mnożyć lub dzielić. Gdy logarytmy mają różne podstawy, przekształć je do wspólnej podstawy, korzystając z odpowiednich wzorów. Po drugie, regularne ćwiczenie zadań matematycznych z logarytmami pomoże w utrwaleniu zasad i zrozumieniu ich zastosowania w różnych kontekstach.
Warto również korzystać z wizualizacji, takich jak wykresy, które mogą pomóc w lepszym zrozumieniu relacji między wartościami logarytmicznymi. Zastosowanie tych praktycznych wskazówek pozwoli na unikanie typowych błędów i skuteczne przekształcanie wyrażeń logarytmicznych. Pamiętaj, że praktyka czyni mistrza, więc im więcej będziesz ćwiczyć, tym lepiej opanujesz mnożenie logarytmów i ich zastosowanie w matematyce.Praktyczne zastosowania logarytmów w analizie danych i programowaniu
Logarytmy mają ogromne znaczenie nie tylko w matematyce, ale również w analizie danych i programowaniu. W kontekście analizy danych, logarytmy są często używane do normalizacji danych, co pozwala na lepsze zrozumienie rozkładów i eliminację wpływu wartości odstających. Na przykład, w przypadku danych finansowych, zastosowanie logarytmu do przekształcenia wartości może pomóc w uzyskaniu bardziej zrównoważonego obrazu trendów, co jest niezwykle ważne w podejmowaniu decyzji inwestycyjnych.
Dodatkowo, w programowaniu, logarytmy są wykorzystywane w algorytmach, takich jak algorytmy wyszukiwania i sortowania. Na przykład, złożoność czasowa algorytmu wyszukiwania binarnego jest opisana za pomocą logarytmu, co oznacza, że przy każdym podziale zbioru danych liczba operacji maleje w tempie logarytmicznym. Zrozumienie zastosowania logarytmów w tych dziedzinach może znacząco wpłynąć na efektywność analizy oraz optymalizację kodu, co czyni je nieocenionym narzędziem w pracy z danymi i programowaniem.

