Logarytm naturalny jest kluczowym pojęciem w matematyce, które odgrywa istotną rolę w wielu dziedzinach nauki. Oznaczany symbolem ln, jest logarytmem o podstawie równej liczbie e (około 2,71828). Ta szczególna liczba pojawia się w różnych zjawiskach matematycznych i fizycznych, co czyni logarytm naturalny niezwykle użytecznym narzędziem w analizie funkcji oraz w modelowaniu procesów wzrostu i rozpadu.
Logarytm naturalny jest również istotny w rachunku różniczkowym, gdzie jego podstawowa właściwość mówi, że pochodna funkcji logarytmu naturalnego wynosi 1/x. Dzięki temu, logarytm naturalny znajduje zastosowanie w wielu dziedzinach, takich jak biologia, ekonomia czy inżynieria. W artykule przyjrzymy się bliżej definicji logarytmu naturalnego, jego zastosowaniom oraz metodom obliczania.Najważniejsze informacje:- Logarytm naturalny to logarytm o podstawie liczby e (około 2,71828).
- Oznaczany jest symbolem ln i jest kluczowy w matematyce oraz naukach przyrodniczych.
- Jest użyteczny w analizie funkcji, rachunku różniczkowym oraz modelowaniu procesów wzrostu i rozpadu.
- Pochodna funkcji logarytmu naturalnego wynosi 1/x, co czyni go istotnym narzędziem w wielu dziedzinach.
- Logarytm naturalny znajduje zastosowanie w biologii, ekonomii, inżynierii i innych naukach.
Co to jest logarytm naturalny i dlaczego jest ważny w matematyce?
Logarytm naturalny to pojęcie, które ma kluczowe znaczenie w matematyce. Jest to logarytm o podstawie równej liczbie e (około 2,71828), która jest niezwykle istotna w różnych dziedzinach nauki. Logarytm naturalny, oznaczany symbolem ln, jest używany do analizy funkcji matematycznych i modelowania zjawisk, takich jak wzrost populacji czy rozpad radioaktywny.
Ważność logarytmu naturalnego wynika z jego zastosowania w rachunku różniczkowym, gdzie pozwala na łatwe obliczanie pochodnych funkcji. Dzięki temu, logarytm naturalny staje się narzędziem niezbędnym dla matematyków, inżynierów i naukowców, którzy muszą analizować złożone zjawiska. W kolejnych sekcjach przyjrzymy się szczegółowo definicji logarytmu naturalnego oraz jego symbolice.Definicja logarytmu naturalnego i jego symbolika
Logarytm naturalny jest definiowany jako logarytm o podstawie liczby e. Oznacza to, że ln(x) to wartość, do której należy podnieść liczbę e, aby uzyskać x. Na przykład, jeśli x wynosi 7, to ln(7) to wartość, która spełnia równanie e^y = 7, gdzie y to wynik logarytmu naturalnego.
Symbol ln jest powszechnie używany w literaturze matematycznej i naukowej, co ułatwia komunikację między naukowcami i studentami. Zrozumienie tego symbolu oraz jego zastosowania jest kluczowe dla dalszego zgłębiania tematów związanych z logarytmem naturalnym.
Rola liczby e w logarytmie naturalnym i jej znaczenie
Liczba e, która wynosi około 2,71828, odgrywa kluczową rolę w kontekście logarytmu naturalnego. Jest to liczba, która pojawia się w wielu dziedzinach matematyki, a jej znaczenie jest szczególnie widoczne w analizie funkcji oraz w rachunku różniczkowym. Logarytm naturalny, oznaczany symbolem ln, jest logarytmem o podstawie e, co oznacza, że dla dowolnej liczby x, logarytm naturalny można zapisać jako ln(x).
W matematyce, liczba e jest fundamentalna, ponieważ ma unikalne właściwości, które ułatwiają obliczenia. Na przykład, funkcja e^x jest jedyną funkcją, której pochodna jest równa samej sobie. Dzięki temu, logarytm naturalny jest niezwykle użyteczny w obliczeniach związanych z pochodnymi i całkami. Zrozumienie roli liczby e jest kluczowe dla dalszego zgłębiania tematów związanych z logarytmem naturalnym oraz jego zastosowaniami w różnych dziedzinach matematyki.
Zastosowania logarytmu naturalnego w różnych dziedzinach
Logarytm naturalny znajduje szerokie zastosowanie w wielu dziedzinach, takich jak nauki przyrodnicze, ekonomia czy inżynieria. Jego właściwości sprawiają, że jest on szczególnie przydatny w modelowaniu zjawisk, które zachowują się w sposób wykładniczy. W biologii, na przykład, logarytm naturalny może być używany do analizy wzrostu populacji, podczas gdy w ekonomii może pomóc w obliczaniu odsetek skomplikowanych.
W inżynierii, logarytm naturalny jest wykorzystywany w procesach związanych z analizą sygnałów czy w teorii informacji. Dzięki swojej uniwersalności, logarytm naturalny jest narzędziem, które pozwala na lepsze zrozumienie i opisanie złożonych zjawisk w różnych dziedzinach. W kolejnych sekcjach artykułu przyjrzymy się szczegółowo zastosowaniom logarytmu naturalnego w praktyce oraz jego właściwościom.
Wykorzystanie logarytmu naturalnego w rachunku różniczkowym
Logarytm naturalny jest niezwykle ważnym narzędziem w rachunku różniczkowym, szczególnie w kontekście obliczania pochodnych funkcji. Jego zastosowanie pozwala na uproszczenie wielu skomplikowanych obliczeń, zwłaszcza gdy mamy do czynienia z funkcjami wykładniczymi. Na przykład, pochodna funkcji ln(x) jest równa 1/x, co jest kluczowym wynikiem w analizie matematycznej.
Dzięki tej właściwości, logarytm naturalny ułatwia obliczanie pochodnych złożonych funkcji, co jest istotne w wielu dziedzinach, takich jak inżynieria czy ekonomia. W praktyce, użycie logarytmu naturalnego w obliczeniach różniczkowych pozwala na lepsze zrozumienie zachowania funkcji i ich ekstremów. W kolejnych sekcjach przyjrzymy się, jak logarytm naturalny znajduje zastosowanie w naukach przyrodniczych.
Przykłady zastosowania logarytmu naturalnego w naukach przyrodniczych
W naukach przyrodniczych, logarytm naturalny jest szeroko stosowany do modelowania różnych zjawisk. Na przykład, w biologii, logarytm naturalny jest używany do analizy wzrostu populacji organizmów, gdzie tempo wzrostu często ma charakter wykładniczy. W fizyce, logarytm naturalny pojawia się w kontekście rozpadu radioaktywnego, gdzie czas połowicznego rozpadu można opisać za pomocą funkcji logarytmicznej.
- Wzrost populacji bakterii można modelować przy użyciu równania N(t) = N0 * e^(rt), gdzie N0 to początkowa liczba bakterii, r to współczynnik wzrostu, a t to czas.
- Rozpad radioaktywny opisuje równanie N(t) = N0 * e^(-λt), gdzie λ to stała rozpadu.
- W chemii, logarytm naturalny jest używany w obliczeniach związanych z pH roztworów, gdzie pH = -ln[H+].
| Dyscyplina | Zastosowanie logarytmu naturalnego |
|---|---|
| Biologia | Modelowanie wzrostu populacji bakterii |
| Fizyka | Analiza rozpadu radioaktywnego |
| Chemia | Obliczenia pH roztworów |
Czytaj więcej: Symbol sumy w matematyce: jak poprawnie stosować notację sigma
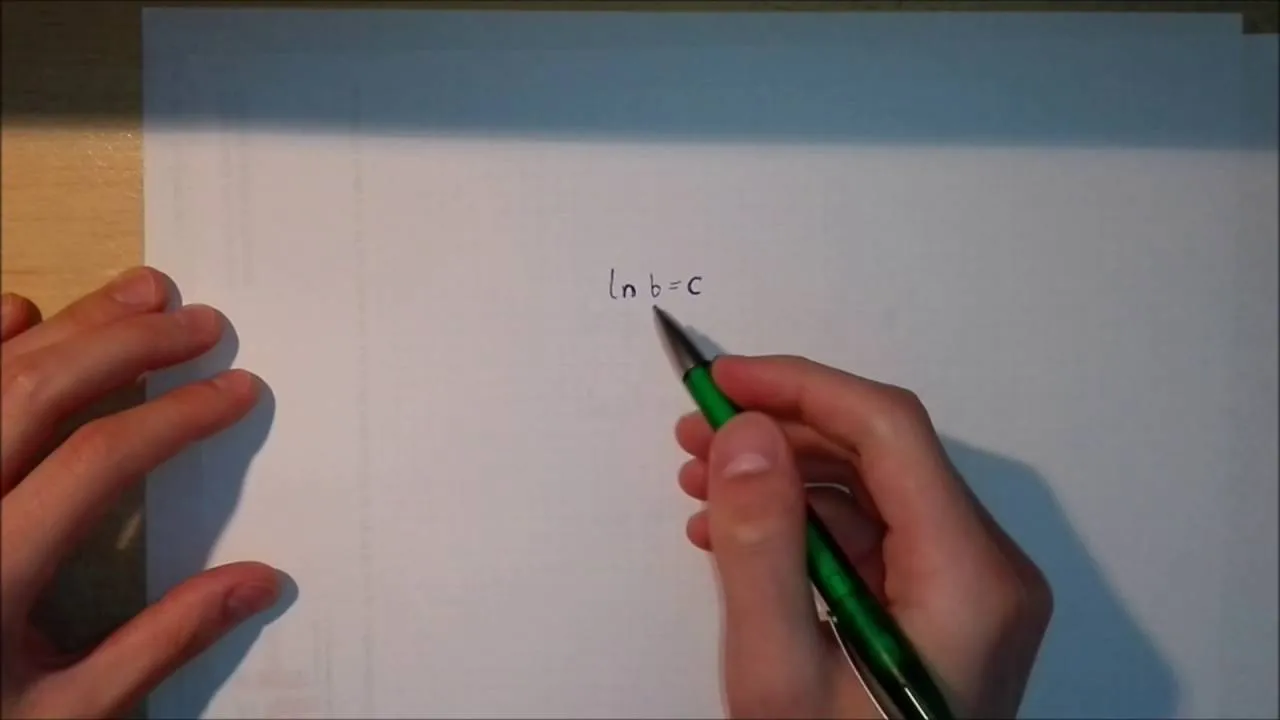
Jak obliczać logarytm naturalny i jego właściwości?

Obliczanie logarytmu naturalnego jest kluczowe w wielu dziedzinach matematyki i nauki. Istnieje kilka metod, które można zastosować do obliczenia wartości ln(x). Najprostszym sposobem jest użycie kalkulatora naukowego, który ma wbudowaną funkcję logarytmu naturalnego. Alternatywnie, logarytm naturalny można obliczyć za pomocą tabel logarytmicznych lub przy użyciu odpowiednich wzorów matematycznych.
Jedną z podstawowych właściwości logarytmu naturalnego jest to, że ln(1) = 0 oraz ln(e) = 1, co stanowi fundament dla dalszych obliczeń. Logarytm naturalny ma również zastosowanie w obliczeniach związanych z pochodnymi funkcji, co czyni go niezwykle przydatnym w analizie matematycznej. W kolejnych sekcjach omówimy konkretne metody obliczania logarytmu naturalnego oraz podamy przykłady.
Metody obliczania logarytmu naturalnego i przykłady
Istnieje kilka metod, które można wykorzystać do obliczania logarytmu naturalnego. Najpopularniejsze z nich to użycie kalkulatorów, które mają funkcję logarytmu naturalnego. Wystarczy wpisać wartość, a kalkulator zwróci wynik. Inną metodą jest korzystanie z tabel logarytmicznych, które zawierają wartości logarytmów dla różnych liczb, co może być szczególnie pomocne w zadaniach bez dostępu do technologii.
Przykładem obliczenia logarytmu naturalnego jest wyznaczenie ln(10). Korzystając z kalkulatora, otrzymujemy wartość około 2,302. Można również obliczyć ln(5), co daje wynik około 1,609. Te wartości są nie tylko użyteczne w matematyce, ale także w zastosowaniach praktycznych, takich jak obliczenia w ekonomii czy naukach przyrodniczych.
Właściwości logarytmu naturalnego i ich praktyczne zastosowanie
Logarytm naturalny ma kilka kluczowych właściwości, które są niezwykle istotne w matematyce i jej zastosowaniach. Po pierwsze, jedna z najważniejszych właściwości to fakt, że ln(ab) = ln(a) + ln(b), co oznacza, że logarytm z iloczynu dwóch liczb jest równy sumie ich logarytmów. Kolejna istotna zasada to ln(a/b) = ln(a) - ln(b), co pozwala na łatwe obliczenia związane z dzieleniem.
Logarytm naturalny jest również funkcją monotonicznie rosnącą, co oznacza, że dla każdej liczby x większej od 0, ln(x) rośnie. Ta właściwość sprawia, że jest on użyteczny w analizie funkcji i optymalizacji. Dzięki tym zasadom, logarytm naturalny znajduje zastosowanie w różnych dziedzinach, takich jak ekonomia, biologia czy inżynieria, umożliwiając modelowanie i rozwiązywanie złożonych problemów.
- Logarytm naturalny jest używany w obliczeniach związanych z pochodnymi funkcji, co czyni go kluczowym w analizie matematycznej.
- Wzory logarytmiczne ułatwiają rozwiązywanie równań wykładniczych, co jest istotne w naukach przyrodniczych.
- Właściwości logarytmu naturalnego są wykorzystywane w statystyce do analizy danych i obliczania rozkładów.
| Właściwość | Opis |
|---|---|
| ln(ab) | Równy sumie logarytmów: ln(a) + ln(b) |
| ln(a/b) | Równy różnicy logarytmów: ln(a) - ln(b) |
| Monotoniczność | Funkcja rośnie dla x > 0 |
Praktyczne zastosowania logarytmu naturalnego w analizie danych
W dobie big data i zaawansowanej analizy danych, logarytm naturalny staje się kluczowym narzędziem w przetwarzaniu i interpretacji informacji. Jego właściwości pozwalają na transformację danych, co jest szczególnie przydatne w modelach regresji i analizie statystycznej. Na przykład, stosowanie logarytmu naturalnego w transformacji zmiennych może pomóc w stabilizacji wariancji i poprawie normalności rozkładu, co jest niezbędne w wielu testach statystycznych.
Dodatkowo, w kontekście uczenia maszynowego, logarytm naturalny jest często wykorzystywany w funkcjach kosztu, takich jak funkcja straty w regresji logistycznej. Dzięki temu, modelowanie złożonych zjawisk staje się bardziej efektywne, a przewidywania dokładniejsze. W przyszłości możemy spodziewać się, że zastosowanie logarytmu naturalnego w analizie danych będzie się rozwijać, szczególnie w obszarach takich jak analiza sentymentu czy przetwarzanie języka naturalnego, gdzie przekształcanie danych w odpowiedni sposób jest kluczowe dla uzyskania wartościowych wyników.




