Liczba e ma wiele interesujących właściwości, w tym to, że jest liczbą niewymierną i przestępną. Może być zdefiniowana na różne sposoby, na przykład jako granica ciągu liczbowego lub jako suma szeregu. W artykule przyjrzymy się bliżej znaczeniu liczby e, jej właściwościom oraz praktycznym zastosowaniom w różnych dziedzinach matematyki.
Kluczowe informacje:- Liczba e jest wartością około 2,718281828459045 i jest kluczowa w matematyce.
- Jest podstawą logarytmu naturalnego oraz funkcji wykładniczej.
- Właściwości liczby e obejmują jej niewymierność i przestępność.
- Liczba e znajduje zastosowanie w analizie matematycznej, fizyce i inżynierii.
- Może być zdefiniowana jako granica ciągu liczbowego lub suma szeregu.
- W notacji naukowej "e" oznacza "razy 10 do potęgi".
Definicja liczby e i jej podstawowe właściwości w matematyce
Liczba e, znana również jako liczba Nepera, jest jedną z najważniejszych stałych w matematyce. Jej wartość wynosi około 2,718281828459045, co czyni ją liczbą niewymierną i przestępną. Liczba e jest fundamentalna w wielu dziedzinach matematyki, będąc podstawą logarytmu naturalnego oraz funkcji wykładniczej. Wartość ta odgrywa kluczową rolę w teorii równań różniczkowych, gdzie pochodna funkcji e^x jest równa samej sobie.Istnieje kilka sposobów na obliczenie liczby e. Można ją zdefiniować jako granicę ciągu liczbowego: lim_{n \to \infty} (1 + \frac{1}{n})^n. Inna metoda to suma szeregu nieskończonego, gdzie e = \sum_{n=0}^{\infty} \frac{1}{n!}. Dzięki tym definicjom, liczba e staje się nie tylko interesującym obiektem matematycznym, ale także narzędziem do rozwiązywania skomplikowanych problemów w analizie matematycznej i innych dziedzinach.
Co to jest liczba e i jak ją obliczyć?
Liczba e jest stałą matematyczną, która znajduje zastosowanie w wielu obszarach. Jej wartość, wynosząca około 2,718281828459045, jest często używana w obliczeniach związanych z funkcjami wykładniczymi. Aby obliczyć liczbę e, można skorzystać z różnych metod, takich jak wspomniana wcześniej granica ciągu liczbowego: lim_{n \to \infty} (1 + \frac{1}{n})^n. Innym sposobem jest wykorzystanie szeregu Taylora, który pozwala na obliczenie e jako sumy nieskończonej.
Właściwości liczby e, które czynią ją wyjątkową
Liczba e ma kilka unikalnych właściwości, które odgrywają kluczową rolę w matematyce. Po pierwsze, jest to liczba niewymierna, co oznacza, że nie można jej wyrazić jako ułamka dwóch liczb całkowitych. Co więcej, liczba e jest również przestępna, co oznacza, że nie jest pierwiastkiem żadnego wielomianu o współczynnikach całkowitych. To sprawia, że liczba ta jest fundamentalna w teorii liczb oraz w analizie matematycznej.
Inną interesującą właściwością liczby e jest jej znaczenie w rachunku różniczkowym. Funkcja wykładnicza e^x ma tę unikalną cechę, że jej pochodna jest równa samej sobie, co sprawia, że jest niezwykle przydatna w rozwiązywaniu równań różniczkowych. Te właściwości liczby e czynią ją nie tylko fascynującym obiektem badań, ale także niezastąpionym narzędziem w różnych dziedzinach matematyki.
Znaczenie liczby e w różnych dziedzinach matematyki
Liczba e odgrywa kluczową rolę w wielu dziedzinach matematyki, a jej znaczenie jest szczególnie widoczne w analizie matematycznej. W kontekście funkcji wykładniczych, liczba e stanowi punkt odniesienia, który umożliwia zrozumienie zachowania funkcji w różnych warunkach. W matematyce, liczba ta jest często wykorzystywana do modelowania zjawisk naturalnych, takich jak wzrost populacji czy procesy finansowe.
W teorii równań różniczkowych, liczba e jest niezastąpiona, ponieważ wiele równań różniczkowych można rozwiązać przy użyciu funkcji wykładniczej. Właściwości liczby e sprawiają, że jest ona nie tylko narzędziem do rozwiązywania problemów, ale także kluczowym elementem w zrozumieniu złożonych systemów matematycznych. Dzięki tym właściwościom, liczba e ma ogromne znaczenie w matematyce i naukach ścisłych.
Rola liczby e w analizie matematycznej i funkcjach wykładniczych
Liczba e odgrywa kluczową rolę w analizie matematycznej, szczególnie w kontekście funkcji wykładniczych. Funkcja wykładnicza e^x jest jedną z najważniejszych funkcji w matematyce, ponieważ ma unikalną właściwość: jej pochodna jest równa samej sobie. To oznacza, że w każdym punkcie funkcja ta zachowuje się w sposób przewidywalny, co jest niezwykle przydatne w różnych dziedzinach matematyki. Dzięki tej właściwości, liczba e jest wykorzystywana do modelowania zjawisk, które rosną w sposób wykładniczy, takich jak populacja czy zyski finansowe.
W analizie matematycznej, liczba e jest także podstawą dla logarytmu naturalnego, co sprawia, że jest niezbędna w wielu obliczeniach. Funkcje wykładnicze o podstawie e są szczególnie ważne w kontekście równań różniczkowych, gdzie pojawiają się w rozwiązaniach wielu praktycznych problemów. Dzięki temu, liczba e jest nie tylko narzędziem teoretycznym, ale także praktycznym w zastosowaniach inżynieryjnych i naukowych.
Zastosowanie liczby e w teorii równań różniczkowych
Liczba e ma fundamentalne znaczenie w teorii równań różniczkowych, gdzie jest kluczowym elementem w rozwiązaniach wielu typów równań. Równania różniczkowe, które opisują zmiany w czasie, często przyjmują formę, w której liczba e pojawia się jako część rozwiązania. Na przykład, w równaniu różniczkowym pierwszego rzędu, rozwiązanie może być wyrażone jako y(t) = Ce^{kt}, gdzie C to stała, a k to współczynnik wzrostu. Takie równania są powszechnie używane w modelowaniu procesów naturalnych, takich jak wzrost populacji czy rozpad radioaktywny.
W praktyce, liczba e umożliwia łatwe obliczenia i przewidywania dotyczące zachowania systemów dynamicznych. Dzięki jej właściwościom, można zrozumieć, jak zmiany w jednym parametrze wpływają na całość systemu, co czyni ją niezastąpioną w analizie matematycznej i inżynieryjnej. W ten sposób, liczba e nie tylko ułatwia rozwiązywanie równań, ale także pozwala na głębsze zrozumienie zjawisk, które są analizowane.
Czytaj więcej: Gdzie znaleźć 17 równań które zmieniły świat w formacie PDF?
Przykłady zastosowań liczby e w praktyce
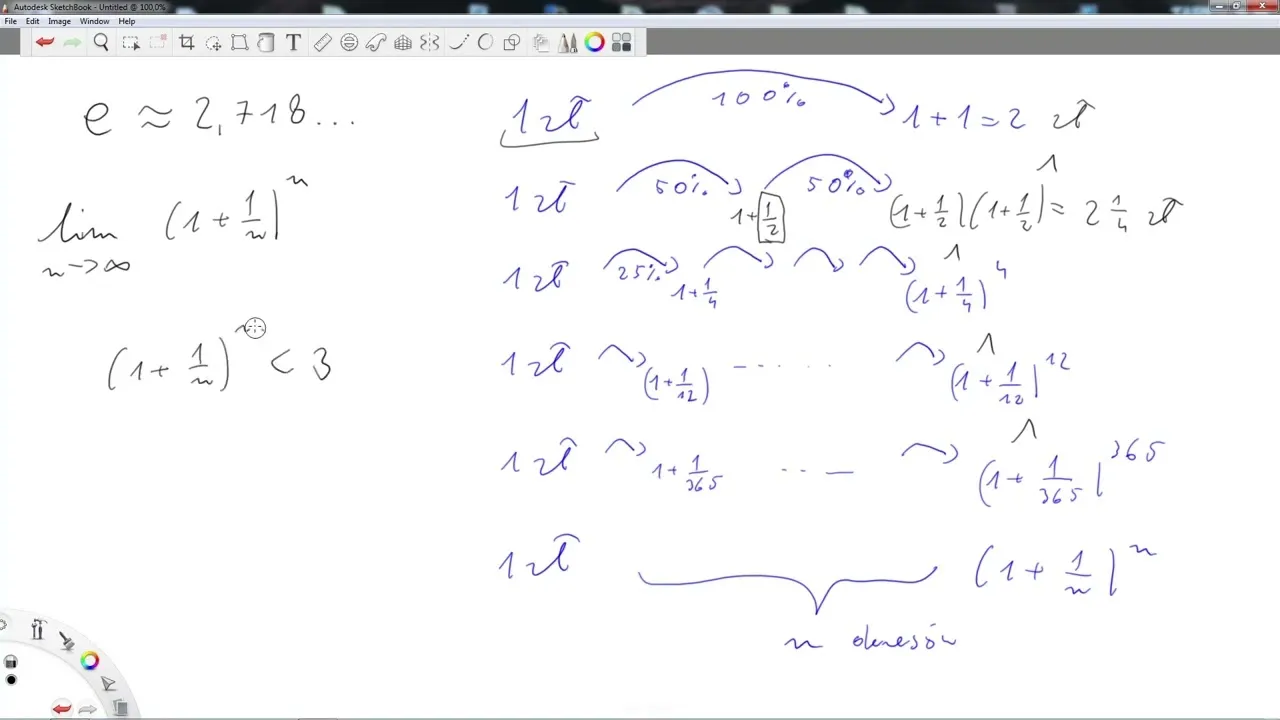
Liczba e znajduje szerokie zastosowanie w różnych dziedzinach życia, w tym w finansach oraz modelowaniu wzrostu populacji. W kontekście finansowym, liczba e jest kluczowa przy obliczeniach związanych z oprocentowaniem składanym. Na przykład, jeśli inwestor zdecyduje się na lokatę, która oferuje roczne oprocentowanie na poziomie 5%, to po roku jego kapitał wzrośnie o 5%. Jednak w przypadku, gdy oprocentowanie jest kapitalizowane częściej, na przykład co miesiąc, użycie liczby e pozwala na dokładniejsze obliczenie finalnej wartości inwestycji.
Wzór na obliczenie wartości inwestycji po czasie t można zapisać jako A = Pe^{rt}, gdzie A to kwota końcowa, P to początkowa kwota inwestycji, r to stopa procentowa, a t to czas w latach. Dzięki zastosowaniu liczby e, inwestorzy mogą lepiej zrozumieć, jak częste kapitalizowanie wpływa na wzrost ich kapitału. W ten sposób liczba e dostarcza praktycznych informacji, które mogą pomóc w podejmowaniu decyzji inwestycyjnych.
Liczba e w modelowaniu wzrostu populacji i finansach
Liczba e jest również niezbędna w modelowaniu wzrostu populacji. W biologii, wzrost populacji często opisuje się za pomocą równania wykładniczego, które wykorzystuje liczbę e. Przykładowo, jeśli populacja pewnego gatunku zwierząt rośnie w tempie 10% rocznie, można to modelować za pomocą wzoru P(t) = P_0 e^{rt}, gdzie P_0 to początkowa liczba osobników, r to współczynnik wzrostu, a t to czas.
W praktyce, ten model pozwala naukowcom przewidzieć, jak populacja będzie się zmieniać w czasie, co jest kluczowe dla zarządzania zasobami naturalnymi oraz ochrony gatunków. Dzięki zastosowaniu liczby e, można uzyskać dokładniejsze prognozy, co w konsekwencji może prowadzić do lepszych strategii ochrony środowiska i zarządzania populacjami. Takie zastosowania liczby e w biologii i ekologii pokazują jej wszechstronność i znaczenie w różnych dziedzinach nauki.
Wykorzystanie liczby e w statystyce i teorii prawdopodobieństwa
Liczba e odgrywa istotną rolę w statystyce oraz teorii prawdopodobieństwa, gdzie jest wykorzystywana w różnych rozkładach prawdopodobieństwa. Na przykład, rozkład normalny, znany również jako rozkład Gaussa, wykorzystuje liczbę e w swoim wzorze, co pozwala na modelowanie wielu zjawisk naturalnych. Wzór na funkcję gęstości prawdopodobieństwa rozkładu normalnego zawiera czynnik e^{- \frac{(x - \mu)^2}{2\sigma^2}}, gdzie μ to średnia, a σ to odchylenie standardowe. Dzięki temu liczba e jest kluczowym elementem w analizie danych i przewidywaniu wyników.
Innym przykładem zastosowania liczby e w statystyce jest rozkład Poissona, który modeluje liczbę zdarzeń występujących w stałym okresie czasu. Wzór tego rozkładu również zawiera liczbę e, co czyni ją niezbędną do obliczania prawdopodobieństwa wystąpienia określonej liczby zdarzeń. W praktyce, liczba e umożliwia analitykom i statystykom dokładniejsze prognozowanie oraz podejmowanie decyzji opartych na danych, co czyni ją niezastąpionym narzędziem w badaniach statystycznych.
Różnice między liczbą e a notacją naukową w matematyce
Liczba e i notacja naukowa to dwa różne koncepty w matematyce, które pełnią różne funkcje. Liczba e jest stałą matematyczną, która ma wartość około 2,71828 i jest używana w kontekście funkcji wykładniczych oraz logarytmów naturalnych. Z kolei notacja naukowa to sposób zapisywania dużych lub małych liczb w formie a × 10^n, gdzie a jest liczbą nie większą niż 10, a n jest liczbą całkowitą. Notacja ta ułatwia obliczenia i przedstawianie wyników w bardziej zrozumiałej formie.
W kontekście obliczeń, liczba e jest używana w różnych wzorach matematycznych, podczas gdy notacja naukowa jest bardziej praktyczna w codziennych obliczeniach oraz prezentacji danych. Na przykład, liczba e może być wykorzystana do obliczeń związanych z funkcjami wykładniczymi, podczas gdy notacja naukowa może być używana do zapisywania wyników obliczeń, takich jak 3,2 × 10^5, co oznacza 320000. Zrozumienie tych różnic jest kluczowe dla efektywnego posługiwania się matematycznymi narzędziami w różnych dziedzinach nauki.
Jak zrozumieć notację e w kontekście obliczeń naukowych?
Liczba e w kontekście obliczeń naukowych jest często używana w połączeniu z notacją naukową, co może być mylące dla niektórych. W notacji naukowej, e oznacza "razy 10 do potęgi", co jest używane do przedstawiania bardzo dużych lub bardzo małych liczb. Na przykład, zapis 3,0e5 oznacza 3,0 × 10^5, co równa się 300000. Wartość ta jest przydatna w różnych obliczeniach, szczególnie w naukach przyrodniczych, gdzie często pracuje się z ekstremalnymi wartościami.
W kontekście obliczeń, liczba e jest również używana w różnych wzorach matematycznych, zwłaszcza w tych dotyczących wzrostu wykładniczego, co może być prezentowane w notacji naukowej. Zrozumienie, jak liczba e współdziała z notacją naukową, pozwala na lepsze zrozumienie obliczeń i ułatwia analizę danych w naukach ścisłych. Dzięki temu, naukowcy i inżynierowie mogą skuteczniej interpretować wyniki swoich badań i podejmować bardziej świadome decyzje.Wykorzystanie liczby e w nowoczesnych technologiach i AI
W miarę jak technologia i sztuczna inteligencja (AI) rozwijają się, liczba e staje się coraz bardziej istotna w zaawansowanych algorytmach uczenia maszynowego. W kontekście analizy danych, liczba e jest kluczowa w funkcjach aktywacji, takich jak funkcja sigmoidalna, która jest używana w sieciach neuronowych. Dzięki zastosowaniu liczby e, modele te są w stanie lepiej przewidywać wyniki, co ma zastosowanie w różnych dziedzinach, od finansów po medycynę.
Co więcej, w obszarze analizy statystycznej, liczba e jest wykorzystywana w zaawansowanych technikach, takich jak modelowanie regresji oraz w algorytmach optymalizacji. W przyszłości możemy spodziewać się, że liczba e będzie miała jeszcze większe znaczenie w kontekście analizy dużych zbiorów danych oraz w tworzeniu bardziej wydajnych algorytmów, które będą w stanie szybko przetwarzać i analizować złożone informacje. W ten sposób, liczba e nie tylko pozostaje fundamentalnym elementem matematyki, ale także staje się kluczowym narzędziem w nowoczesnych technologiach i innowacjach.
