Znajomość kątów jest nie tylko istotna w teorii, ale również w praktyce, na przykład w architekturze czy inżynierii. Zrozumienie ich klasyfikacji oraz relacji między nimi, takich jak kąty przyległe czy wierzchołkowe, może pomóc w rozwiązywaniu problemów geometrycznych oraz w projektowaniu różnych struktur. W dalszej części artykułu omówimy szczegółowo te zagadnienia oraz ich zastosowanie w różnych dziedzinach.
Najważniejsze informacje:
- Kąt to część płaszczyzny wyznaczona przez dwie półproste o wspólnym początku.
- Rodzaje kątów obejmują kąty zerowe, ostre, proste, rozwarte, półpełne i pełne.
- Kąty klasyfikowane są na podstawie ich miary, co ułatwia ich zrozumienie.
- Kąty przyległe mają wspólne ramię i suma ich miar wynosi 180°.
- Kąty wierzchołkowe mają wspólny wierzchołek i są zawsze równe.
- Kąty mają zastosowanie w architekturze i inżynierii, wpływając na obliczenia i konstrukcje.
- W geometrii kąty są kluczowe przy obliczaniu sumy kątów w różnych figurach geometrycznych.
Kąty w matematyce: Definicje i podstawowe pojęcia
Kąty są kluczowym elementem w matematyce, szczególnie w geometrii. Definiuje się je jako część płaszczyzny, która jest wyznaczona przez dwie półproste o wspólnym początku. Ten wspólny początek nazywamy wierzchołkiem kąta, a półproste te to ramiona kąta. Kąt można również opisać jako część wspólną dwóch półpłaszczyzn, które są oddzielone przez nierównoległe proste. Dzięki tej definicji możemy zrozumieć, jak kąty są używane do opisu przestrzeni i form geometrycznych.
Kąty odgrywają istotną rolę w matematyce, ponieważ są podstawą wielu konstrukcji i obliczeń. W matematyce klasyfikacja kątów opiera się głównie na ich miarze. Kąty wypukłe, na przykład, mają miarę mniejszą lub równą 180°, podczas gdy kąty wklęsłe mają miarę większą niż 180°, ale mniejszą niż 360°. Oznaczanie kątów za pomocą małych liter greckich, takich jak α (alfa) czy β (beta), jest powszechne i ułatwia ich identyfikację w różnych kontekstach. Zrozumienie tych podstawowych definicji jest kluczowe dla dalszego zgłębiania tematu kątów w matematyce.
Czym są kąty i jak je definiujemy w matematyce?
Kąty można zdefiniować jako przestrzeń między dwiema półprostymi, które mają wspólny początek. Wierzchołek kąta to punkt, w którym te półproste się spotykają. Ramiona kąta to z kolei te półproste, które tworzą kąt. Wartością miary kąta jest kąt, który powstaje między tymi ramionami. W matematyce używamy różnych jednostek miary kątów, z których najpopularniejsze to stopnie oraz radiany.
W matematyce kąty są reprezentowane graficznie, co pozwala na ich lepsze zrozumienie. Przykładowo, rysując kąt, można zobaczyć, jak ramiona kąta oddzielają dwie półpłaszczyzny. Tego typu wizualizacje są niezwykle pomocne w nauczaniu i zrozumieniu pojęcia kątów, a także w dalszym rozwoju umiejętności geometrycznych.
Jakie są różne rodzaje kątów i ich miary?
W matematyce istnieje wiele różnych rodzajów kątów, które różnią się swoją miarą i właściwościami. Każdy z tych rodzajów kątów w matematyce ma swoje unikalne cechy, które są istotne w wielu zastosowaniach geometrycznych. Zrozumienie tych różnic jest kluczowe dla dalszego poznawania geometrii i jej zastosowań. Poniżej przedstawiamy najważniejsze rodzaje kątów oraz ich miary.
Każdy kąt można zmierzyć w stopniach, a jego wartość określa, do jakiego rodzaju należy. Kąty klasyfikowane są na podstawie ich miar, co pozwala na ich łatwe zrozumienie i zastosowanie w praktyce. W tej sekcji omówimy sześć podstawowych typów kątów i ich miary, które są fundamentem dla dalszej nauki o właściwościach kątów w matematyce.Rodzaje kątów i ich miary
- Kąt zerowy – miara równa 0°. Jest to kąt, w którym ramiona pokrywają się, co oznacza, że nie tworzy on żadnej przestrzeni.
- Kąt ostry – miara większa od 0°, ale mniejsza od 90°. Kąty ostre mają zastosowanie w wielu dziedzinach, takich jak architektura i inżynieria.
- Kąt prosty – miara równa dokładnie 90°. Kąt prosty jest podstawowym elementem w geometrii, szczególnie w konstrukcjach prostokątnych.
- Kąt rozwarty – miara większa od 90°, ale mniejsza od 180°. Kąty te są często spotykane w różnych figurach geometrycznych.
- Kąt półpełny – miara równa 180°. Kąt ten dzieli płaszczyznę na dwie równe półpłaszczyzny.
- Kąt pełny – miara równa 360°. Kąt pełny obejmuje pełen obrót wokół wierzchołka, tworząc zamkniętą pętlę.
Kąty ostre, proste, rozwarte i pełne: Co je odróżnia?
Kąty można klasyfikować na różne sposoby, a jednym z najważniejszych podziałów jest ten oparty na ich miarze. Kąty ostre mają miarę większą od 0° i mniejszą od 90°. Są to kąty, które tworzą wrażenie "ostrości" i często występują w wielu zastosowaniach, takich jak projektowanie. Z kolei kąty proste mają miarę dokładnie 90°. To klasyczny kąt, który jest podstawą wielu konstrukcji, szczególnie w architekturze i inżynierii. Warto zauważyć, że kąty proste są często używane jako punkt odniesienia w różnych obliczeniach geometrycznych.
W dalszej klasyfikacji, kąty rozwarte mają miarę większą od 90°, ale mniejszą od 180°. Są one szersze niż kąty proste i mogą być używane w różnych kontekstach, takich jak w rysunkach technicznych. Ostatnim typem, który omówimy, jest kąt pełny, który ma miarę 360°. Kąt pełny to kąt, który obejmuje pełen obrót wokół wierzchołka, co oznacza, że jego ramiona pokrywają się. Zrozumienie tych różnic jest kluczowe dla dalszej nauki o kątach w matematyce.
Kąty przyległe i wierzchołkowe: Właściwości i przykłady
Kąty przyległe to dwa kąty, które mają wspólne ramię i wierzchołek, a ich suma miar wynosi zawsze 180°. Przykładem mogą być kąty, które tworzą się w wyniku przecięcia dwóch prostych. Kąty przyległe są istotne w geometrii, ponieważ pozwalają na określenie relacji między kątami w różnych figurach. Dzięki nim możemy lepiej zrozumieć, jak kąty współdziałają ze sobą w ramach danej figury.
Innym ważnym rodzajem kątów są kąty wierzchołkowe, które powstają, gdy dwie linie przecinają się, tworząc dwa zestawy kątów. Kąty te mają wspólny wierzchołek i są zawsze równe. Na przykład, jeśli jedna z linii tworzy kąt 30°, to kąt wierzchołkowy po drugiej stronie również będzie miał miarę 30°. Zrozumienie tych właściwości jest kluczowe dla analizy bardziej złożonych problemów geometrycznych.
Zastosowania kątów w praktyce: Jak wykorzystujemy je na co dzień?
Kąty odgrywają kluczową rolę w wielu dziedzinach, takich jak architektura i inżynieria, gdzie ich zastosowanie jest niezbędne do tworzenia stabilnych i funkcjonalnych struktur. W architekturze kąty są wykorzystywane do projektowania budynków, mostów i innych obiektów, zapewniając odpowiednią stabilność i estetykę. Na przykład, w przypadku budynków mieszkalnych, kąty prostokątne są kluczowe dla zapewnienia prawidłowego rozmieszczenia pomieszczeń oraz ich funkcjonalności. Bez precyzyjnych kątów, projektowanie i budowa obiektów stałoby się znacznie trudniejsze.
W inżynierii kąty są również istotne w obliczeniach dotyczących sił działających na konstrukcje. Na przykład, w przypadku mostów, inżynierowie muszą dokładnie obliczyć kąty, aby zapewnić równomierne rozłożenie obciążenia. Kąty są także wykorzystywane w mechanice do określenia kierunku ruchu oraz w projektowaniu systemów, takich jak dźwigi czy windy. Zrozumienie zastosowania kątów w praktyce pozwala na lepsze projektowanie i optymalizację różnych systemów inżynieryjnych, co przekłada się na ich efektywność i bezpieczeństwo.
Kąty w architekturze i inżynierii: Przykłady zastosowań
W architekturze, kąty są kluczowe w tworzeniu estetycznych i funkcjonalnych przestrzeni. Na przykład, w projekcie słynnego budynku Burj Khalifa w Dubaju, zastosowano różne kąty, aby osiągnąć jego unikalny kształt i wysokość. Kąt nachylenia fasady tego wieżowca nie tylko nadaje mu charakterystyczny wygląd, ale także pomaga w zarządzaniu wiatrem i innymi czynnikami atmosferycznymi. Dzięki precyzyjnym obliczeniom kątów, architekci mogą tworzyć innowacyjne projekty, które są zarówno piękne, jak i funkcjonalne.
W inżynierii, kąty mają kluczowe znaczenie w projektowaniu mostów, takich jak Most Golden Gate w San Francisco. Kąty użyte w konstrukcji mostu pozwalają na efektywne rozłożenie obciążenia, co jest niezbędne dla jego stabilności. Inżynierowie muszą dokładnie obliczyć kąty, aby zapewnić, że most wytrzyma różne siły, takie jak ciężar pojazdów oraz wiatr. Przykłady te pokazują, jak istotne są kąty w praktycznych zastosowaniach, wpływając na bezpieczeństwo i funkcjonalność różnych struktur.
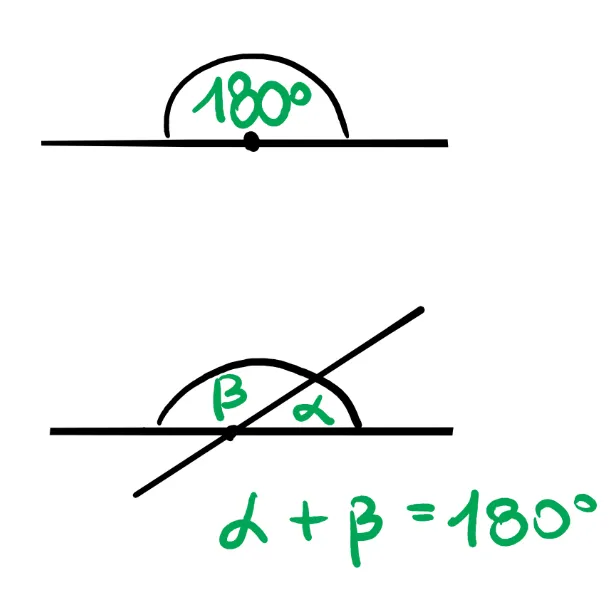
Kąty w geometrii: Jak wpływają na obliczenia i konstrukcje?
Kąty odgrywają kluczową rolę w geometrii, wpływając na różne obliczenia i konstrukcje. Ich miara jest istotna w określaniu powierzchni figur geometrycznych, takich jak trójkąty czy czworokąty. Na przykład, w przypadku trójkąta, suma miar wszystkich kątów wynosi zawsze 180°. To fundamentalne założenie pozwala na obliczenie brakujących kątów, co jest niezbędne w wielu zastosowaniach praktycznych. Ponadto, kąty są również istotne przy obliczaniu objętości i powierzchni brył, takich jak sześciany czy ostrosłupy.
W konstrukcjach inżynieryjnych, precyzyjne pomiary kątów są niezbędne do zapewnienia stabilności i bezpieczeństwa. Na przykład, w budowie mostów, inżynierowie muszą uwzględnić kąty, aby obliczyć obciążenia działające na konstrukcję. Wykorzystując odpowiednie kąty, można zoptymalizować rozkład sił, co przekłada się na dłuższą żywotność budowli. Zrozumienie roli kątów w obliczeniach geometrycznych jest kluczowe dla każdego, kto pracuje w dziedzinach związanych z architekturą i inżynierią.
Innowacyjne zastosowania kątów w projektowaniu 3D i VR
W dzisiejszych czasach, kąty odgrywają kluczową rolę nie tylko w tradycyjnej geometrii, ale także w nowoczesnym projektowaniu 3D oraz technologii wirtualnej rzeczywistości (VR). W tych dziedzinach, precyzyjne obliczenia kątów są niezbędne do tworzenia realistycznych modeli i symulacji. Na przykład, w projektowaniu gier komputerowych, kąty są używane do definiowania perspektywy kamery oraz interakcji obiektów w przestrzeni 3D, co znacząco wpływa na doświadczenia użytkowników.
Co więcej, technologie takie jak druk 3D wykorzystują kąty do optymalizacji struktur, co pozwala na tworzenie lekkich, ale mocnych konstrukcji. Dzięki zastosowaniu zaawansowanych algorytmów, inżynierowie mogą analizować, jak zmiana kątów wpływa na trwałość i funkcjonalność wydrukowanych obiektów. W miarę jak technologia się rozwija, możemy oczekiwać, że zastosowanie kątów w takich innowacyjnych obszarach będzie się jeszcze bardziej rozwijać, prowadząc do nowych możliwości w projektowaniu i inżynierii.




