Czeski błąd w matematyce to termin odnoszący się do przestawienia dwóch ostatnich cyfr w liczbie, co może prowadzić do poważnych pomyłek w obliczeniach. Tego rodzaju błąd często występuje podczas szybkiego pisania lub wpisywania danych na klawiaturze. Na przykład, zamieniając ostatnie dwie cyfry liczby 8590, otrzymujemy 8509, a różnica między tymi dwoma wartościami zawsze dzieli się przez 9. Zrozumienie tego błędu jest kluczowe, ponieważ może on znacząco wpłynąć na wyniki matematyczne, zwłaszcza w kontekście mnożenia i innych operacji arytmetycznych.
W praktyce, czeski błąd może być trudny do zauważenia, ponieważ przestawienie cyfr nie zawsze wpływa na wartość liczbową w oczywisty sposób. Warto jednak wiedzieć, jak go unikać, aby nie prowadził do kosztownych pomyłek. W tym artykule przyjrzymy się definicji czeskiego błędu, jego wpływowi na obliczenia oraz skutecznym metodom, które pomogą w jego unikaniu.Kluczowe wnioski:- Czeski błąd polega na przestawieniu dwóch ostatnich cyfr w liczbie.
- Różnica między liczbą oryginalną a zmienioną zawsze dzieli się przez 9.
- Błąd ten może prowadzić do błędnych wyników w obliczeniach, szczególnie w mnożeniu.
- Przykłady czeskiego błędu można znaleźć w różnych dziedzinach, takich jak finanse i inżynieria.
- Istnieją skuteczne metody, aby unikać czeskiego błędu, takie jak dokładne sprawdzanie wyników.
- Czeski błąd wpływa na proces nauki matematyki, utrudniając zrozumienie i dokładność obliczeń.
Czeski błąd w matematyce: definicja i znaczenie w obliczeniach
Czeski błąd w matematyce to termin, który odnosi się do przestawienia dwóch ostatnich cyfr w liczbie. Tego rodzaju błąd często występuje podczas szybkiego pisania lub wpisywania liczb na klawiaturze, co może prowadzić do poważnych pomyłek w obliczeniach. Na przykład, jeśli weźmiemy liczbę 8590 i zamienimy ostatnie dwie cyfry, otrzymamy 8509. Różnica między tymi dwiema wartościami wynosi 81, a co ważne, zawsze dzieli się przez 9. Zrozumienie tego błędu jest kluczowe, ponieważ może on znacząco wpłynąć na wyniki matematyczne, zwłaszcza w kontekście mnożenia i innych operacji arytmetycznych.
W praktyce, czeski błąd może być trudny do zauważenia, ponieważ przestawienie cyfr w liczbie nie zawsze wpływa na wartość liczbową w oczywisty sposób. Jednakże, jeśli nie zostanie dostrzeżony, może prowadzić do błędnych wyników, co jest szczególnie istotne w dziedzinach takich jak finanse czy inżynieria. Dlatego ważne jest, aby każdy, kto pracuje z liczbami, był świadomy istnienia czeskiego błędu i jego potencjalnych konsekwencji w obliczeniach.
Przykłady czeskiego błędu w praktycznych obliczeniach
W praktyce, czeski błąd w matematyce może mieć poważne konsekwencje, zwłaszcza w dziedzinach takich jak finanse czy inżynieria. Na przykład, w finansach, jeśli księgowy przez przypadek zamieni cyfry w kwocie 1 250 na 1 520, może to prowadzić do błędnych raportów finansowych. Tego rodzaju pomyłki mogą skutkować niewłaściwymi decyzjami inwestycyjnymi, które mogą narazić firmę na straty. Dlatego tak ważne jest, aby być świadomym możliwości wystąpienia czeskiego błędu w codziennych obliczeniach.
Inny przykład można znaleźć w inżynierii, gdzie dokładność obliczeń jest kluczowa. Jeśli inżynier oblicza obciążenie konstrukcji i przez przypadek wprowadzi błędnie wartość 5 400 kg zamiast 4 300 kg, może to prowadzić do poważnych problemów strukturalnych. Tego typu błędy mogą mieć katastrofalne skutki, dlatego ważne jest, aby stosować odpowiednie metody weryfikacji wyników, aby unikać czeskiego błędu.
| Numer oryginalny | Numer z czeskim błędem | Różnica | Skutki |
|---|---|---|---|
| 1250 | 1520 | 270 | Błędne raporty finansowe |
| 4300 | 5400 | 1000 | Problemy strukturalne w budowie |
Typowe sytuacje, w których występuje czeski błąd
Czeski błąd często występuje w sytuacjach, gdzie pośpiech i nieuwaga mogą prowadzić do pomyłek. Przykłady obejmują szybkie wprowadzanie danych do systemów komputerowych, gdzie pracownicy mogą przypadkowo zamienić cyfry. Inne typowe sytuacje to obliczenia wykonywane podczas rozmów telefonicznych, gdzie liczby są podawane ustnie, co zwiększa ryzyko błędów. W takich przypadkach, warto stosować metody weryfikacji, aby upewnić się, że wprowadzone dane są poprawne.
Czytaj więcej: Jak się liczy skalę w matematyce? Proste przykłady i wyjaśnienia
Jak unikać czeskiego błędu w matematyce podczas obliczeń?
Aby skutecznie unikać czeskiego błędu w matematyce, kluczowe jest wprowadzenie kilku prostych, ale efektywnych strategii. Przede wszystkim, podwójne sprawdzanie wyników może znacząco zmniejszyć ryzyko wystąpienia tego błędu. Kiedy wprowadzamy dane, warto zawsze zweryfikować, czy cyfry zostały poprawnie zapisane. Może to być tak proste, jak ponowne przeczytanie wartości lub skorzystanie z narzędzi, które automatycznie sprawdzają poprawność wprowadzonych danych. W praktyce, takie działania mogą uratować nas przed kosztownymi pomyłkami.
Innym skutecznym sposobem na unikanie czeskiego błędu jest korzystanie z kalkulatorów lub programów komputerowych, które minimalizują ryzyko błędów w obliczeniach. Wiele nowoczesnych aplikacji do obliczeń matematycznych oferuje funkcje, które automatycznie sprawdzają wprowadzone dane i sugerują poprawki. Dzięki temu możemy mieć pewność, że nasze obliczenia są dokładne, a potencjalne błędy zostaną wykryte na wczesnym etapie. Warto także zainwestować czas w naukę korzystania z takich narzędzi, co przyniesie korzyści w dłuższej perspektywie.
Skuteczne metody na sprawdzanie poprawności wyników
Weryfikacja wyników obliczeń jest kluczowym elementem unikania czeskiego błędu. Istnieje wiele metod, które można zastosować, aby upewnić się, że nasze obliczenia są poprawne. Cross-checking, czyli sprawdzanie wyników poprzez porównanie ich z innymi danymi, jest jedną z najskuteczniejszych technik. Możemy również korzystać z szacowania wyników, co pozwala na szybkie zweryfikowanie, czy nasze obliczenia mieszczą się w oczekiwanym zakresie. Tego rodzaju techniki są niezwykle pomocne w codziennej pracy z liczbami.
- Podwójne sprawdzanie: zawsze weryfikuj wprowadzone dane, aby uniknąć błędów.
- Korzystanie z kalkulatorów: używaj narzędzi, które automatycznie sprawdzają poprawność wyników.
- Cross-checking: porównuj wyniki z innymi danymi, aby upewnić się, że są poprawne.
- Szacowanie: szybko weryfikuj, czy wyniki mieszczą się w oczekiwanym zakresie.
Czeski błąd a inne matematyczne pomyłki: różnice i podobieństwa
Czeski błąd w matematyce jest jednym z wielu błędów, które mogą wystąpić podczas obliczeń. W przeciwieństwie do błędów zaokrągleń, które wynikają z przybliżenia wartości liczbowych, czeski błąd polega na przestawieniu cyfr, co prowadzi do całkowicie innej wartości. Na przykład, w przypadku liczby 1234, przestawienie cyfr na 1324 zmienia wynik obliczenia, co może mieć poważne konsekwencje, zwłaszcza w kontekście finansowym. Różnica między tymi błędami polega na tym, że czeski błąd jest często wynikiem nieuwagi, a błędy zaokrągleń są związane z metodami obliczeniowymi.
Inną istotną różnicą jest to, że czeski błąd może być trudniejszy do zauważenia podczas weryfikacji wyników. W przypadku błędów zaokrągleń, można łatwo sprawdzić, czy wynik jest w rozsądnych granicach, natomiast czeski błąd może prowadzić do wartości, które są nadal logiczne, ale całkowicie błędne. Błędy obliczeniowe, takie jak błędy w dodawaniu lub mnożeniu, również różnią się od czeskiego błędu, ponieważ wynik tych błędów wynika z niewłaściwego zastosowania reguł matematycznych, a nie z przestawienia cyfr. Zrozumienie tych różnic jest kluczowe, aby skutecznie unikać różnych typów błędów w matematyce.
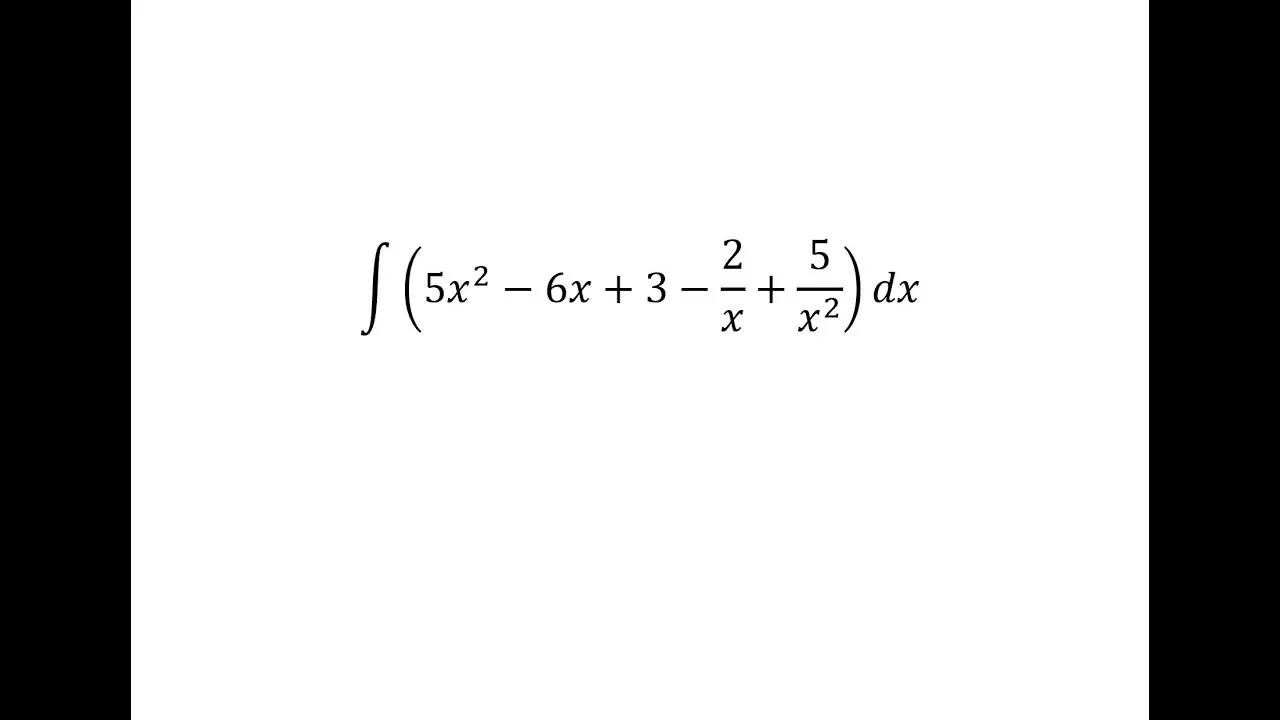
Jak czeski błąd wpływa na proces nauki matematyki?
Czeski błąd w matematyce ma istotny wpływ na proces nauki, zwłaszcza wśród uczniów i studentów. Kiedy uczniowie popełniają ten błąd, często nie zdają sobie sprawy z tego, że ich wyniki są błędne, co może prowadzić do nieporozumień w zrozumieniu materiału. Tego rodzaju pomyłki mogą zniechęcać do dalszej nauki, ponieważ uczniowie mogą czuć się zagubieni i mniej pewni swoich umiejętności matematycznych. W konsekwencji, czeski błąd może wpływać na ich samoocenę oraz motywację do nauki przedmiotów ścisłych.Ważne jest, aby nauczyciele i rodzice byli świadomi wpływu, jaki czeski błąd może mieć na naukę. Dobrze jest wprowadzać metody weryfikacji wyników, aby uczniowie nauczyli się sprawdzać swoje obliczenia. Umożliwi to lepsze zrozumienie zasad matematycznych oraz pomoże w budowaniu pewności siebie w obliczeniach. W ten sposób można zminimalizować negatywne skutki czeskiego błędu, a uczniowie będą bardziej skłonni do podejmowania wyzwań związanych z nauką matematyki.
Jak technologia może pomóc w eliminacji czeskiego błędu?
W erze cyfrowej, technologia odgrywa kluczową rolę w minimalizowaniu ryzyka wystąpienia czeskiego błędu w matematyce. Aplikacje mobilne i programy komputerowe do nauki matematyki często oferują funkcje, które automatycznie weryfikują wprowadzone dane i obliczenia. Dzięki temu użytkownicy mogą szybko zidentyfikować błędy i poprawić je zanim przejdą do dalszych obliczeń. Wprowadzenie takich narzędzi do codziennej praktyki uczniów i profesjonalistów może znacznie zwiększyć dokładność obliczeń oraz zbudować pewność siebie w pracy z liczbami.
Co więcej, uczenie maszynowe i sztuczna inteligencja mogą być wykorzystane do analizy typowych błędów popełnianych przez użytkowników. Systemy te mogą dostarczać spersonalizowane rekomendacje dotyczące poprawy umiejętności matematycznych na podstawie analizy wcześniejszych błędów. Przykładowo, jeśli program zauważy, że użytkownik często myli cyfry w określonych warunkach, może zasugerować dodatkowe ćwiczenia lub techniki, które pomogą w przezwyciężeniu tych trudności. Takie podejście nie tylko zwiększa efektywność nauki, ale także czyni ją bardziej interaktywną i angażującą.





