System dziesiętny jest fundamentalnym elementem matematyki, który odgrywa kluczową rolę w codziennym życiu. Jest to system liczbowy oparty na dziesięciu cyfrach: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. Dzięki temu, że wartości cyfr zależą od ich pozycji, możemy tworzyć różnorodne liczby. Użycie przecinka jako separatora między częścią całkowitą a ułamkową pozwala na łatwe zapisywanie i interpretowanie liczb dziesiętnych.
W artykule przyjrzymy się bliżej historii systemu dziesiętnego, jego zastosowaniom oraz temu, jak ułamki dziesiętne wpływają na nasze codzienne obliczenia. Zrozumienie tych zasad jest nie tylko istotne dla uczniów, ale także dla każdego, kto pragnie lepiej zrozumieć podstawy matematyki.
Kluczowe informacje:
- System dziesiętny jest pozycyjnym systemem liczbowym opartym na dziesięciu cyfrach.
- Ułamki dziesiętne to zapis ułamków zwykłych z mianownikiem będącym potęgą liczby 10.
- System dziesiętny ma swoje korzenie w starożytnych cywilizacjach, takich jak Sumerowie i Indie.
- W codziennym życiu ułamki dziesiętne są używane w finansach, pomiarach i wielu innych dziedzinach.
- Porównanie systemu dziesiętnego z innymi systemami liczbowymi, takimi jak binarny, ujawnia jego unikalne zalety.
- Wiele osób ma błędne przekonania na temat ułamków dziesiętnych, które warto wyjaśnić.
Zrozumienie systemu dziesiętnego w matematyce i jego znaczenie
System dziesiętny, znany również jako system dziesiątkowy lub system arabski, jest podstawowym systemem liczbowym, który wykorzystujemy na co dzień. Opiera się na dziesięciu cyfrach: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. Wartość każdej cyfry w liczbie zależy od jej pozycji, co oznacza, że każda cyfra jest mnożona przez odpowiednią potęgę liczby 10. Dzięki temu systemowi możemy efektywnie przedstawiać i obliczać liczby, co czyni go niezwykle użytecznym w matematyce.
Wartością wyróżniającą system dziesiętny jest jego prostota i intuicyjność. Umożliwia on łatwe wykonywanie podstawowych działań matematycznych, takich jak dodawanie, odejmowanie, mnożenie i dzielenie. Zrozumienie zasad działania systemu dziesiętnego jest kluczowe nie tylko dla uczniów, ale także dla każdego, kto chce lepiej zrozumieć matematykę i jej zastosowania w życiu codziennym. Dlatego tak ważne jest, aby poznać jego podstawowe zasady i zastosowania.Definicja systemu dziesiętnego i jego podstawowe zasady
System dziesiętny jest systemem pozycyjnym, co oznacza, że każda cyfra ma wartość w zależności od swojej pozycji w liczbie. Na przykład w liczbie 345, cyfra 3 reprezentuje trzysta (3 x 100), cyfra 4 reprezentuje czterdzieści (4 x 10), a cyfra 5 to pięć (5 x 1). System ten wykorzystuje separator dziesiętny, zazwyczaj przecinek, do oddzielania części całkowitej od ułamkowej. Ułamek dziesiętny jest zapisywany w formie, gdzie mianownik jest potęgą liczby 10, co ułatwia jego zrozumienie i obliczenia.
Jak działa zapis liczb dziesiętnych i ich wartości
Zapis liczb dziesiętnych opiera się na systemie pozycyjnym, co oznacza, że każda cyfra ma wartość uzależnioną od jej pozycji w liczbie. W systemie dziesiętnym wykorzystujemy separator dziesiętny, zazwyczaj przecinek, aby oddzielić część całkowitą od ułamkowej. Na przykład w liczbie 45,67, cyfra 4 znajduje się w pozycji dziesiątek, co oznacza, że reprezentuje 40, a cyfra 5 to 5 jednostek. Część po przecinku, czyli 67, pokazuje wartości ułamkowe, gdzie 6 to 6 dziesiątych, a 7 to 7 setnych. Dzięki temu systemowi możemy w prosty sposób przedstawiać zarówno liczby całkowite, jak i ułamki.Historia systemu dziesiętnego: Od Sumerów do dzisiaj
Historia systemu dziesiętnego sięga starożytnych cywilizacji, w tym Sumerów, którzy jako pierwsi zaczęli używać systemu pozycyjnego. Z czasem, system ten ewoluował i był rozwijany przez różne kultury, w tym Egipcjan i Greków. Kluczowym momentem w historii systemu dziesiętnego było wprowadzenie zera jako wartości, co znacznie ułatwiło wykonywanie obliczeń. System dziesiętny zyskał na popularności dzięki swojej prostocie i efektywności w porównaniu do innych systemów liczbowych.
W miarę upływu czasu, system dziesiętny dotarł do Indii, gdzie został znacznie rozwinięty przez matematyka Brahmaguptę. Z Indii system ten rozprzestrzenił się do Europy, głównie dzięki Arabom, którzy przetłumaczyli i rozpowszechnili wiedzę matematyczną. W rezultacie, system dziesiętny stał się podstawowym systemem liczbowym używanym w większości krajów na całym świecie, co miało ogromny wpływ na rozwój nauki i technologii.
Ewolucja systemu dziesiętnego w różnych kulturach
System dziesiętny ma swoje korzenie w starożytnych cywilizacjach, które przyczyniły się do jego rozwoju. Sumerowie, żyjący około 3100 roku p.n.e., jako pierwsi zaczęli stosować system pozycyjny, który stanowił fundament dla późniejszych systemów liczbowych. W Egipcie i Babilonii rozwijano różne metody obliczeń, które wykorzystywały zasady systemu dziesiętnego, jednak to Indowie wprowadzili kluczowe innowacje, takie jak zero, które znacznie uprościło obliczenia. Z czasem, system dziesiętny przyjął się w Europie, a jego zasady zostały spopularyzowane przez arabskich uczonych, co miało ogromny wpływ na rozwój matematyki w średniowieczu.
Wpływ Indii i Arabów na rozwój systemu dziesiętnego
Indyjscy matematycy mieli kluczowy wpływ na rozwój systemu dziesiętnego, wprowadzając koncepcję zera jako wartości, co zrewolucjonizowało sposób obliczania. Brahmagupta, jeden z najważniejszych indyjskich matematyków, wprowadził zasady dotyczące operacji na liczbach z zerem. Arabowie, przetłumaczywszy indyjskie teksty matematyczne, przyczynili się do dalszego rozwoju systemu dziesiętnego, wprowadzając go do Europy. Dzięki ich pracy, system dziesiętny stał się powszechnie stosowany w zachodniej matematyce, co miało ogromny wpływ na naukę i technologię w późniejszych wiekach.
Ułamki dziesiętne: Przykłady i zastosowania w praktyce
Ułamki dziesiętne to liczby, które są wyrażane w formie dziesiętnej, co oznacza, że mają część całkowitą oraz część ułamkową oddzieloną przecinkiem. W codziennym życiu ułamki dziesiętne są niezwykle użyteczne, ponieważ pozwalają na precyzyjne przedstawienie wartości, które nie są całkowite. Na przykład, w finansach, ceny produktów są często zapisywane jako ułamki dziesiętne, takie jak 19,99 zł. Aby zamienić ułamek zwykły na dziesiętny, wystarczy podzielić licznik przez mianownik, co ułatwia obliczenia i porównania wartości.
Użycie ułamków dziesiętnych ma wiele praktycznych zastosowań, od obliczeń w sklepie po pomiary w naukach przyrodniczych. W kuchni, na przykład, przepisy często wymagają precyzyjnych ilości składników, które można zapisać jako ułamki dziesiętne, takie jak 0,5 litra mleka. Dzięki systemowi dziesiętnemu, obliczenia stają się prostsze i bardziej zrozumiałe, co czyni go kluczowym narzędziem w różnych dziedzinach życia.
Jak zamieniać ułamki zwykłe na dziesiętne i odwrotnie
Proces zamiany ułamków zwykłych na ułamki dziesiętne jest prosty i polega na podzieleniu licznika przez mianownik. Na przykład, aby zamienić ułamek 1/4 na ułamek dziesiętny, dzielimy 1 przez 4, co daje nam 0,25. Z kolei, aby zamienić ułamek dziesiętny na ułamek zwykły, możemy zidentyfikować miejsce przecinka. Na przykład, liczba 0,75 można zapisać jako 75/100, co po uproszczeniu daje 3/4. Te proste metody pozwalają na łatwe przechodzenie między różnymi formami zapisu liczb, co jest przydatne w wielu sytuacjach.
| Ułamek zwykły | Ułamek dziesiętny |
| 1/2 | 0,5 |
| 3/4 | 0,75 |
| 1/5 | 0,2 |
| 2/3 | 0,6667 |
Przykłady zastosowania ułamków dziesiętnych w codziennym życiu
Ułamki dziesiętne znajdują szerokie zastosowanie w codziennym życiu, szczególnie w dziedzinach takich jak finanse i pomiary. Na przykład, w sklepach ceny produktów często są wyrażane w formie ułamków dziesiętnych, takich jak 29,99 zł za produkt, co ułatwia zakupy i porównania cen. W kuchni, przepisy kulinarne mogą wymagać precyzyjnych ilości składników, jak 0,5 litra mleka lub 0,25 szklanki cukru, co pomaga w dokładnym przygotowaniu potraw. Ułamki dziesiętne są również powszechnie używane w naukach przyrodniczych, gdzie pomiary długości, masy czy objętości są często wyrażane w formie dziesiętnej, co zwiększa dokładność wyników.
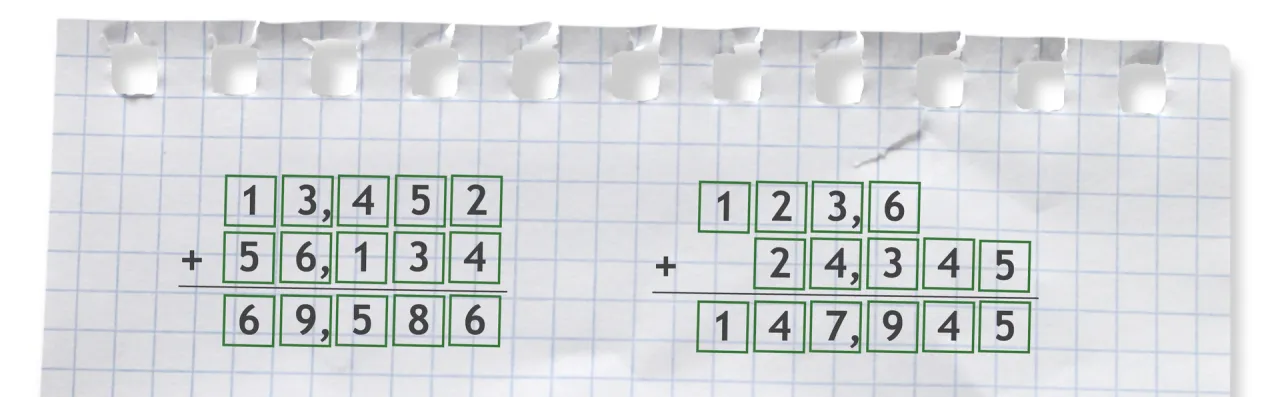
Porównanie systemu dziesiętnego z innymi systemami liczbowymi
System dziesiętny, w przeciwieństwie do systemów takich jak binarny czy ósemkowy, oparty jest na dziesięciu cyfrach, co czyni go bardziej intuicyjnym dla większości ludzi. W systemie binarnym, który używa tylko dwóch cyfr (0 i 1), liczby są reprezentowane w sposób bardziej skomplikowany, co może być trudniejsze do zrozumienia dla osób, które nie są zaznajomione z informatyką. Dzięki temu, że system dziesiętny jest powszechnie stosowany w codziennych obliczeniach, jego zalety stają się oczywiste, zwłaszcza w kontekście prostoty i efektywności w wykonywaniu podstawowych działań matematycznych.
Warto również zauważyć, że system dziesiętny ma przewagę w zastosowaniach praktycznych, ponieważ jest bardziej zrozumiały dla ludzi w porównaniu do systemów, takich jak ósemkowy, który używa ośmiu cyfr (0-7). W praktyce, to oznacza, że obliczenia w systemie dziesiętnym są szybsze i łatwiejsze do wykonania, co ma kluczowe znaczenie w sytuacjach wymagających szybkich decyzji, takich jak zakupy czy obliczenia w naukach przyrodniczych. Dlatego system dziesiętny jest nie tylko podstawowym systemem używanym w matematyce, ale także najbardziej praktycznym w codziennym życiu.
Przyszłość systemu dziesiętnego: Innowacje i nowe zastosowania
W miarę jak technologia się rozwija, system dziesiętny zyskuje nowe zastosowania, które mogą zrewolucjonizować sposób, w jaki postrzegamy i używamy liczb. Przykładem jest integracja uczenia maszynowego i sztucznej inteligencji w aplikacjach finansowych, gdzie ułamki dziesiętne są wykorzystywane do analizy danych i prognozowania trendów rynkowych. Dzięki precyzyjnym obliczeniom opartym na ułamkach dziesiętnych, inwestorzy mogą podejmować bardziej świadome decyzje, co zwiększa efektywność operacji na giełdzie oraz w zarządzaniu portfelem.
Co więcej, w kontekście Internetu Rzeczy (IoT), system dziesiętny odgrywa kluczową rolę w zbieraniu i przetwarzaniu danych z różnych urządzeń. Użycie ułamków dziesiętnych w pomiarach, takich jak temperatura, wilgotność czy ciśnienie, pozwala na dokładniejsze monitorowanie i analizowanie warunków w czasie rzeczywistym. W przyszłości możemy spodziewać się jeszcze większej integracji systemu dziesiętnego w codziennym życiu, co przyczyni się do dalszego uproszczenia obliczeń i zwiększenia precyzji w różnych dziedzinach, takich jak medycyna, inżynieria czy zarządzanie danymi.





