Zrozumienie zadań tekstowych z równaniami może być wyzwaniem, ale z odpowiednim podejściem staje się znacznie prostsze. Kluczowym krokiem jest ustalenie niewiadomej, co pozwala na systematyczne podejście do problemu. W tym artykule przedstawimy proste kroki, które pomogą Ci w rozwiązywaniu zadań tekstowych, a także zaprezentujemy przykłady, które ułatwią zrozumienie tego tematu.
Podczas rozwiązywania zadań, ważne jest, aby umieć tworzyć równania na podstawie treści zadania oraz właściwie interpretować podane informacje. Dzięki temu, będziesz w stanie nie tylko znaleźć rozwiązanie, ale także upewnić się, że jest ono poprawne. Pamiętaj, że każdy krok jest istotny, aby ostatecznie sformułować odpowiedź na postawione pytanie.
Najistotniejsze informacje:
- Określenie niewiadomej jest pierwszym krokiem w rozwiązywaniu zadań tekstowych.
- Tworzenie równań z treści zadania pozwala na systematyczne podejście do problemu.
- W zadaniach dotyczących wieku można oznaczyć wiek ojca jako x, a syna jako y.
- W przypadku zadań o liczbie przedmiotów, warto ustalić, ile przedmiotów jest w danym zadaniu.
- Najczęstsze błędy wynikają z niewłaściwej interpretacji treści zadania.
- Sprawdzanie rozwiązań jest kluczowe, aby upewnić się, że odpowiedź jest poprawna.
Jak zrozumieć zadania tekstowe z równaniami - kluczowe kroki
Aby zrozumieć zadania tekstowe z równaniami, warto postępować według określonego schematu, który ułatwia systematyczne podejście do problemu. Kluczowym krokiem jest ustalenie niewiadomej, co pozwala na późniejsze tworzenie odpowiednich równań. Dzięki temu, będziesz w stanie przeanalizować treść zadania i wyodrębnić istotne informacje, które są niezbędne do rozwiązania. Prawidłowe zrozumienie problemu jest fundamentem, na którym opiera się dalszy proces rozwiązywania.
Po zidentyfikowaniu niewiadomej, kolejnym krokiem jest tworzenie równań na podstawie treści zadania. Umożliwia to zapisanie problemu w formie matematycznej, co jest niezbędne do jego analizy i rozwiązania. Warto pamiętać, że każdy krok w tym procesie jest istotny, ponieważ pozwala na zbudowanie logicznego ciągu myślowego, który prowadzi do ostatecznego rozwiązania. Właściwe podejście do zadań tekstowych sprawia, że stają się one bardziej zrozumiałe i mniej stresujące.
Określenie niewiadomej - pierwszy krok do rozwiązania
Określenie niewiadomej jest kluczowym etapem w rozwiązywaniu zadań tekstowych. Właściwe zidentyfikowanie niewiadomej pozwala na skupienie się na istotnych elementach problemu i ułatwia późniejsze tworzenie równań. Warto oznaczyć niewiadomą literą, na przykład x, co uprości dalsze działania i pozwoli na lepsze zrozumienie relacji między danymi w zadaniu.
- Używaj liter, takich jak x, y, czy z, aby oznaczyć niewiadome.
- Sprawdź, czy w treści zadania pojawiają się informacje, które mogą pomóc w ustaleniu, co oznacza niewiadoma.
- W przypadku zadań z wieloma niewiadomymi, staraj się wyodrębnić każdą z nich, aby uniknąć zamieszania.
Tworzenie równań z treści zadania - jak to zrobić?
Aby skutecznie tworzyć równania z treści zadania, należy najpierw dokładnie przeanalizować podane informacje. Kluczowe jest, aby zrozumieć, co dana treść oznacza i jakie relacje między danymi występują. Po zidentyfikowaniu niewiadomych, można przystąpić do zapisywania równań, które odzwierciedlają sytuację opisaną w zadaniu. Pamiętaj, że każde równanie powinno być logicznie powiązane z informacjami zawartymi w treści, co ułatwi dalsze rozwiązywanie problemu.
Podczas tworzenia równań warto stosować różne techniki, takie jak używanie symboli i liter do oznaczania niewiadomych oraz tworzenie równań na podstawie relacji między danymi. Umożliwia to zapisanie problemu w formie algebraicznej, co jest niezbędne do jego analizy. Kluczowe jest, aby upewnić się, że wszystkie istotne informacje zostały uwzględnione, co pozwoli na dokładne rozwiązanie zadania.
| Typ problemu | Przykładowe równanie |
|---|---|
| Wiek (ojciec i syn) | x + 5 = y |
| Liczba przedmiotów (krowy i kaczki) | x + y = 170 |
| Podział pieniędzy | x + 2y = 100 |
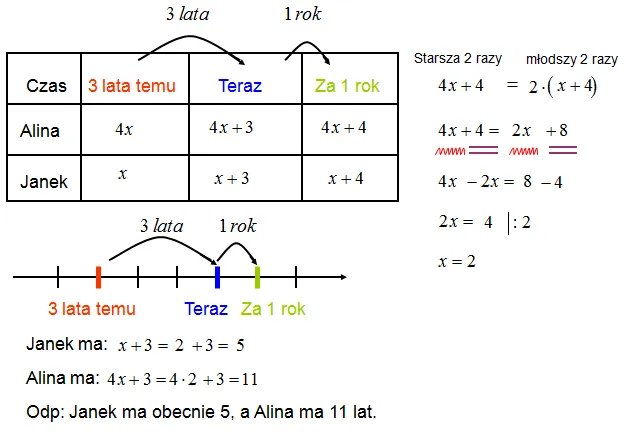
Zadania dotyczące wieku - praktyczne przykłady i rozwiązania
Zadania dotyczące wieku często opierają się na relacjach między osobami, takimi jak ojciec i syn. Zwykle w takich problemach pojawiają się informacje o wieku w różnych momentach czasu, co pozwala na stworzenie równań. Typowy format tych zadań może obejmować stwierdzenia takie jak "za pięć lat ojciec będzie dwa razy starszy od syna". Kluczowe jest, aby umieć zidentyfikować, które zmienne będą niewiadomymi, co pozwoli na skonstruowanie odpowiednich równań.
Przykład: Załóżmy, że wiek ojca oznaczymy jako x, a wiek syna jako y. Z treści zadania możemy wywnioskować, że "za 5 lat ojciec będzie miał 5 lat więcej, a syn również 5 lat więcej". Możemy zatem zapisać równanie: x + 5 = 2(y + 5). Rozwiązując to równanie, mamy:
x + 5 = 2y + 10
x - 2y = 5.
Zadania o liczbie przedmiotów - jak tworzyć równania?
Zadania o liczbie przedmiotów zazwyczaj koncentrują się na ilościach, takich jak liczba jabłek, krów czy innych obiektów. W takich problemach kluczowe jest ustalenie, jakie relacje istnieją między różnymi typami przedmiotów. Na przykład, jeśli mamy 170 zwierząt na łące, z których część to krowy, a część to kaczki, możemy oznaczyć liczbę krów jako x, a liczbę kaczek jako 170 - x. To pozwoli nam na stworzenie równań, które odzwierciedlają sytuację opisaną w zadaniu.
Przykład: Jeśli w treści zadania stwierdzono, że krowy mają 4 nogi, a kaczki 2 nogi, możemy stworzyć równanie dotyczące całkowitej liczby nóg. Równanie będzie wyglądać następująco: 4x + 2(170 - x) = 680. Rozwiązując to równanie, uzyskujemy: 4x + 340 - 2x = 680, co upraszcza się do 2x = 340, a zatem x = 170. Oznacza to, że wszystkie zwierzęta na łące to krowy.
Najczęstsze pułapki w zadaniach tekstowych z równaniami
Podczas rozwiązywania zadań tekstowych z równaniami, wiele osób napotyka na typowe pułapki, które mogą prowadzić do błędnych odpowiedzi. Jedną z najczęstszych pomyłek jest niewłaściwa interpretacja treści zadania. Często zdarza się, że kluczowe informacje są przeoczone lub źle zrozumiane, co prowadzi do błędnego sformułowania równań. Aby tego uniknąć, warto dokładnie analizować każde zdanie i zwracać uwagę na szczegóły, które mogą mieć znaczenie dla rozwiązania.
Inną powszechną pułapką jest niedokładne sprawdzanie rozwiązań. Po rozwiązaniu równania, wielu uczniów zapomina zweryfikować, czy uzyskane odpowiedzi spełniają warunki zadania. To może prowadzić do sytuacji, w której odpowiedź wydaje się poprawna, ale w rzeczywistości nie jest zgodna z treścią problemu. Aby temu zapobiec, zawsze warto wrócić do treści zadania i upewnić się, że rozwiązanie jest logiczne i sensowne w kontekście postawionego pytania.
Błędy w interpretacji treści - jak ich unikać?
Dokładna analiza treści zadania jest kluczowa, aby uniknąć błędów w interpretacji. Często zdarza się, że uczniowie przeoczą istotne informacje lub źle zrozumieją, co jest wymagane w danym problemie. Niewłaściwe zrozumienie treści może prowadzić do błędnego sformułowania równań i, w efekcie, do błędnych odpowiedzi. Aby tego uniknąć, warto przywiązywać dużą wagę do starannego czytania i analizowania każdego zdania, a także zwracać uwagę na kluczowe słowa i wyrażenia, które mogą zmieniać sens zadania.
- "W ciągu" - może oznaczać różne okresy czasu, co wpływa na interpretację.
- "Za" - często wskazuje na przyszłość i wymaga uwzględnienia zmian w czasie.
- "Razem" - może sugerować dodawanie, ale w kontekście zadania może oznaczać coś innego.
- "O ile" - wymaga zrozumienia relacji między różnymi danymi w zadaniu.
Sprawdzanie rozwiązań - klucz do pewności w odpowiedziach
Weryfikacja rozwiązań jest niezbędna, aby upewnić się, że odpowiedzi są poprawne. Po rozwiązaniu zadania warto wrócić do treści problemu i sprawdzić, czy uzyskane rozwiązanie spełnia wszystkie wymagane warunki. Można to zrobić poprzez podstawienie uzyskanych wartości do równań i upewnienie się, że są one zgodne z danymi z treści zadania. Na przykład, jeśli w zadaniu dotyczącym wieku otrzymaliśmy, że syn ma 12 lat, a ojciec 30, warto sprawdzić, czy te liczby pasują do relacji przedstawionej w treści.
Jak rozwijać umiejętności rozwiązywania zadań tekstowych?
Aby rozwinąć umiejętności rozwiązywania zadań tekstowych, warto wprowadzić różnorodne techniki praktyczne, które pomogą w lepszym zrozumieniu i interpretacji problemów. Jednym z podejść jest regularne ćwiczenie zadań z różnych dziedzin, co pozwala na rozpoznawanie wzorców i relacji między danymi. Można również korzystać z aplikacji edukacyjnych i platform online, które oferują interaktywne ćwiczenia oraz natychmiastowe informacje zwrotne, co sprzyja szybszemu przyswajaniu wiedzy.
Dodatkowo, warto angażować się w dyskusje grupowe na temat zadań tekstowych. Wspólne rozwiązywanie problemów z rówieśnikami może prowadzić do wymiany pomysłów oraz zrozumienia różnych podejść do tych samych zadań. Uczestnictwo w warsztatach lub kursach online również może wzbogacić umiejętności i dostarczyć nowych strategii, które będą przydatne w przyszłych wyzwaniach matematycznych. Im więcej praktyki i różnorodnych doświadczeń, tym łatwiej będzie radzić sobie z coraz bardziej złożonymi problemami.





