Zakreskowanie liczby będącej rozwiązaniem równania to kluczowy krok w nauce matematyki, który pozwala zrozumieć, jak działa algebra. W artykule omówimy, jak poprawnie identyfikować rozwiązania równań oraz jak je zaznaczać. Nie tylko przedstawimy przykłady konkretnych równań, ale także wyjaśnimy, co oznaczają poszczególne litery przypisane do tych rozwiązań.
Przykłady równań, takie jak 2(x + 4) = 6x czy -3x + 7 = -5x - 1, pomogą nam zrozumieć, jak znaleźć odpowiednie liczby i przyporządkować im odpowiednie litery. Dzięki temu każdy, kto chce nauczyć się matematyki, będzie mógł skutecznie zaznaczać rozwiązania i lepiej rozumieć tę dziedzinę.
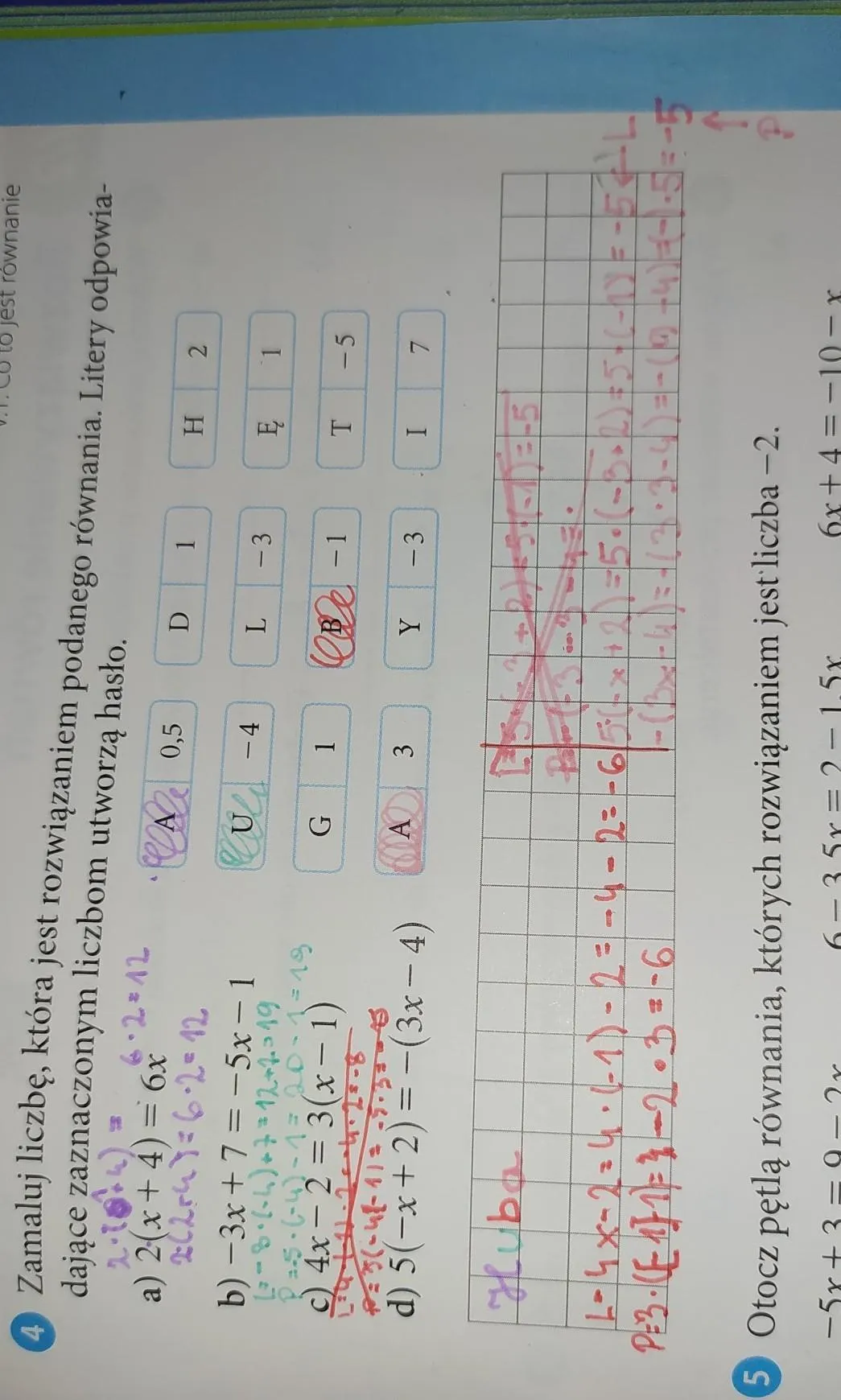
Kluczowe informacje:- Rozwiązanie równania 2(x + 4) = 6x to liczba 2, oznaczona literą H.
- W równaniu -3x + 7 = -5x - 1 rozwiązaniem jest liczba -4, co odpowiada literze U.
- Równanie 4x - 2 = 3(x - 1) ma rozwiązanie -1, przypisane literze B.
- W przypadku równania 5(-x + 2) = -(3x - 4) rozwiązaniem jest liczba 3, co odpowiada literze A.
- Umiejętność zaznaczania rozwiązań jest istotna dla zrozumienia równań w matematyce.
Jak skutecznie zakreskować rozwiązanie równania matematycznego
Umiejętność zakreskowania liczby będącej rozwiązaniem równania jest kluczowa w matematyce. Właściwe identyfikowanie rozwiązań pozwala na lepsze zrozumienie równań i ich zastosowania w różnych dziedzinach. Kiedy potrafimy zaznaczyć odpowiednie liczby, stajemy się bardziej pewni siebie w rozwiązywaniu problemów matematycznych.
W matematyce istnieje wiele rodzajów równań, a każde z nich ma swoje unikalne rozwiązania. Zrozumienie, jak je znaleźć i oznaczyć, jest istotne nie tylko dla uczniów, ale także dla osób pracujących w dziedzinach technicznych i naukowych. Dzięki temu możemy skutecznie analizować dane i podejmować lepsze decyzje oparte na wynikach naszych obliczeń.
Zrozumienie równań i ich rozwiązań dla lepszego podejścia
Równania matematyczne to wyrażenia, które pokazują relacje między różnymi zmiennymi. Każde równanie ma swoje rozwiązanie, które jest wartością zmiennej, która sprawia, że równanie jest prawdziwe. Wyróżniamy różne typy równań, takie jak liniowe, kwadratowe czy wielomianowe, a każde z nich wymaga innego podejścia do rozwiązania.
Znajomość różnych typów równań oraz ich rozwiązań jest kluczowa dla efektywnego uczenia się matematyki. Dzięki temu możemy zrozumieć, jak różne zmienne wpływają na siebie nawzajem. Właściwe podejście do równań pozwala na łatwiejsze i szybsze znajdowanie odpowiedzi na złożone problemy matematyczne, co jest szczególnie przydatne w naukach ścisłych oraz inżynierii.Kluczowe kroki do rozwiązania równań matematycznych
Rozwiązywanie równań matematycznych może wydawać się skomplikowane, ale istnieją kluczowe kroki, które ułatwiają ten proces. Pierwszym krokiem jest zrozumienie struktury równania. Ważne jest, aby wiedzieć, jakie elementy są w równaniu i jakie operacje można na nich przeprowadzić. Ułatwia to dalsze działania i pozwala na uniknięcie pomyłek.Następnie, należy przenieść wszystkie wyrazy z jedną zmienną na jedną stronę równania. Może to wymagać dodawania lub odejmowania wyrazów. Po uporządkowaniu równań można przystąpić do dalszych obliczeń, co pozwala na wyizolowanie zmiennej. To kluczowy moment, w którym zaczynamy widzieć, jaką wartość przyjmuje zmienna.
Praktyczne kroki do rozwiązania równań
W kolejnym kroku warto stosować odpowiednie operacje matematyczne, takie jak mnożenie lub dzielenie, aby uprościć równanie. Upewnij się, że wykonujesz te operacje na obu stronach równania, aby zachować równowagę. To ważne, aby nie pomijać żadnego kroku, ponieważ może to prowadzić do błędnych wyników.
- Dokładnie analizuj każdy krok rozwiązania, aby upewnić się, że nie popełniasz błędów.
- W przypadku bardziej skomplikowanych równań, rozważ użycie metod graficznych lub numerycznych.
- Nie zapominaj o sprawdzeniu swojego rozwiązania, podstawiając je z powrotem do oryginalnego równania.
Czytaj więcej: Jak się liczy logarytmy? Prosty sposób na zrozumienie obliczeń
Analiza równania 2(x + 4) = 6x i jego rozwiązanie
Równanie 2(x + 4) = 6x jest przykładem równania liniowego, które możemy rozwiązać krok po kroku. Na początku przekształcamy równanie, aby uprościć jego formę. Rozpoczynamy od rozłożenia nawiasów: 2x + 8 = 6x. Następnie przenosimy wszystkie wyrazy z x na jedną stronę równania, co daje nam 8 = 6x - 2x.
Po uproszczeniu otrzymujemy 8 = 4x. Teraz wystarczy podzielić obie strony przez 4, aby uzyskać wartość x = 2. To oznacza, że rozwiązaniem równania jest liczba 2, co odpowiada literze H.
Zrozumienie równania -3x + 7 = -5x - 1 i jego wynik
Przyjrzyjmy się teraz równaniu -3x + 7 = -5x - 1. Na początku przekształcamy równanie, aby uprościć jego formę. Przenosimy wszystkie wyrazy z x na jedną stronę, co daje nam -3x + 5x = -1 - 7.
Po uproszczeniu otrzymujemy 2x = -8. Następnie, dzieląc obie strony przez 2, uzyskujemy x = -4. W ten sposób rozwiązaniem równania jest liczba -4, co odpowiada literze U.
Jak identyfikować rozwiązania w równaniach matematycznych
Identyfikacja rozwiązań w równaniach matematycznych jest kluczowym umiejętnością, która pozwala na efektywne rozwiązywanie problemów. Istnieje wiele metod, które można zastosować, aby znaleźć rozwiązania, w tym podejścia graficzne i numeryczne. Wizualizacja równań może być niezwykle pomocna, zwłaszcza w przypadku bardziej skomplikowanych problemów, które nie zawsze są łatwe do rozwiązania analitycznie. Jedną z najczęściej stosowanych metod jest wykres funkcji, który pozwala na zobaczenie, gdzie funkcja przecina oś X. To właśnie w tych punktach znajdują się rozwiązania równania. Inne podejścia, takie jak metody numeryczne, mogą być używane, gdy rozwiązania nie mogą być znalezione w sposób analityczny. Te metody wykorzystują algorytmy, które przybliżają rozwiązania na podstawie danych wejściowych.Techniki rozwiązywania równań liniowych dla początkujących
Rozwiązywanie równań liniowych może być prostsze, gdy zastosujemy odpowiednie techniki. Substytucja to jedna z podstawowych metod, która polega na zastąpieniu jednej zmiennej inną, aby uprościć równanie. Dzięki temu możemy łatwiej znaleźć wartość zmiennej, a proces staje się bardziej przejrzysty.
Inną popularną techniką jest eliminacja, która polega na dodawaniu lub odejmowaniu równań, aby wyeliminować jedną ze zmiennych. To podejście pozwala na uzyskanie prostszego równania, które można łatwo rozwiązać. Używając tych technik, początkujący uczniowie mogą skutecznie odnaleźć rozwiązania równań liniowych, co stanowi solidną podstawę do dalszej nauki matematyki.
Wskazówki dotyczące wizualizacji rozwiązań równań
Wizualizacja rozwiązań równań jest kluczowym elementem w nauce matematyki, który pomaga zrozumieć, jak różne zmienne wpływają na siebie nawzajem. Wykresy i diagramy mogą znacznie ułatwić interpretację danych oraz identyfikację punktów, w których równania mają swoje rozwiązania. Dzięki wizualizacji, uczniowie mogą lepiej zrozumieć pojęcia, które mogą wydawać się abstrakcyjne w formie algebraicznej.
Aby stworzyć skuteczne wizualizacje, warto zacząć od prostych wykresów, które pokazują, jak zmieniają się wartości zmiennych w zależności od siebie. Można używać programów komputerowych, takich jak Excel czy GeoGebra, które oferują narzędzia do rysowania wykresów. Warto również eksperymentować z różnymi typami wykresów, takimi jak wykresy liniowe, słupkowe czy punktowe, aby zobaczyć, która forma najlepiej ilustruje dane rozwiązania.
| Typ wizualizacji | Opis | Efektywność |
| Wykres liniowy | Pokazuje zmiany wartości w czasie lub w zależności od innej zmiennej. | Wysoka, szczególnie w przypadku funkcji liniowych. |
| Wykres słupkowy | Używany do porównania różnych wartości w zbiorze danych. | Średnia, dobry do porównań między różnymi grupami. |
| Wykres punktowy | Ilustruje relacje między dwiema zmiennymi. | Wysoka, szczególnie w analizie korelacji. |
Jak wykorzystać wizualizacje do rozwiązywania problemów matematycznych
Wizualizacje równań nie tylko ułatwiają zrozumienie rozwiązań, ale również mogą być używane jako potężne narzędzie w rozwiązywaniu rzeczywistych problemów matematycznych. Analiza danych przy użyciu wykresów pozwala na szybsze identyfikowanie trendów i wzorców, co jest szczególnie przydatne w dziedzinach takich jak ekonomia, inżynieria czy nauki przyrodnicze. Przykładowo, w analizie finansowej, wizualizacje mogą pomóc inwestorom w ocenie ryzyka i potencjalnych zysków z różnych inwestycji.
Dodatkowo, w erze rozwoju technologii, wykorzystanie zaawansowanych narzędzi do wizualizacji, takich jak programy do modelowania 3D czy aplikacje do wizualizacji danych w czasie rzeczywistym, staje się coraz bardziej popularne. Umożliwiają one nie tylko przedstawienie skomplikowanych równań w przystępnej formie, ale także symulację różnych scenariuszy, co może być kluczowe w podejmowaniu decyzji w czasie rzeczywistym. Takie podejście otwiera nowe możliwości w edukacji oraz w praktycznych zastosowaniach w przemyśle i badaniach naukowych.





