Ile wysokości ma trójkąt? To pytanie może wydawać się proste, ale ma istotne znaczenie w geometrii. Każdy trójkąt ma trzy wysokości, które są odcinkami łączącymi wierzchołki trójkąta z prostą zawierającą przeciwległy bok, a także prostopadłymi do tej prostej. Wysokości te, lub ich przedłużenia, spotykają się w jednym punkcie, który nazywamy ortocentrum. Zrozumienie tego pojęcia jest kluczowe dla dalszego zgłębiania geometrii i jej zastosowań.
W artykule przyjrzymy się nie tylko definicji wysokości w trójkącie, ale również sposobom ich obliczania w różnych typach trójkątów. Zrozumienie tych zagadnień pomoże lepiej zrozumieć, jak funkcjonują trójkąty i jakie mają właściwości geometryczne.
Najistotniejsze informacje:- Każdy trójkąt ma trzy wysokości, które są kluczowe dla jego analizy geometrycznej.
- Wysokość to odcinek łączący wierzchołek z przeciwległym bokiem, prostopadły do tego boku.
- Wysokości trójkąta przecinają się w punkcie zwanym ortocentrum.
- Obliczanie wysokości różni się w zależności od rodzaju trójkąta: równobocznego, prostokątnego i różnobocznego.
- Ortocentrum ma istotne znaczenie w geometrii, ponieważ łączy różne aspekty trójkątów.
Ile wysokości ma trójkąt i jak je zdefiniować?
Każdy trójkąt ma trzy wysokości, które są kluczowe dla zrozumienia jego geometrii. Wysokość w trójkącie to odcinek łączący wierzchołek z przeciwległym bokiem, prostopadły do tego boku. To właśnie dzięki wysokościom możemy określić różne właściwości trójkąta, takie jak jego pole. Wysokości mają istotne znaczenie, ponieważ ich długości oraz wzajemne relacje mogą pomóc w dalszym analizowaniu trójkątów.
Wysokości trójkąta, a także ich przedłużenia, spotykają się w jednym punkcie, który nazywamy ortocentrum. Zrozumienie, ile wysokości ma trójkąt, oraz ich definicji, jest fundamentalne dla dalszego zgłębiania geometrii. Każda wysokość jest unikalna dla danego wierzchołka, co sprawia, że trójkąty różnią się między sobą nie tylko kształtem, ale również właściwościami geometrycznymi.
Zrozumienie pojęcia wysokości w trójkącie i ich znaczenie
Wysokość trójkąta to kluczowy element, który pomaga w analizie jego struktury. Wysokości są nie tylko istotne dla obliczeń, ale także dla zrozumienia, jak trójkąty funkcjonują w przestrzeni. Dzięki nim możemy określić pole trójkąta oraz inne ważne właściwości. Wysokości odgrywają również rolę w różnych zastosowaniach praktycznych, takich jak inżynieria czy architektura, gdzie precyzyjne pomiary są niezbędne.
Trzy wysokości w trójkącie: jak są zbudowane?
W każdym trójkącie znajdują się trzy wysokości, które mają kluczowe znaczenie dla jego analizy geometrycznej. Każda z tych wysokości jest odcinkiem, który łączy wierzchołek trójkąta z prostą zawierającą przeciwległy bok, a jednocześnie jest prostopadły do tej prostej. Wysokość z wierzchołka A prowadzi do boku BC, wysokość z wierzchołka B prowadzi do boku AC, a wysokość z wierzchołka C prowadzi do boku AB. W ten sposób każda wysokość jest związana z jednym z wierzchołków trójkąta i jego przeciwległym bokiem.
Wysokości te, lub ich przedłużenia, spotykają się w punkcie, który nazywamy ortocentrum. Zrozumienie, jak są zbudowane te trzy wysokości, pozwala lepiej zrozumieć właściwości trójkąta oraz jego zachowanie w różnych kontekstach geometrycznych. Dzięki temu możemy również analizować, jak zmieniają się te wysokości w zależności od kształtu trójkąta.
Jak obliczyć wysokości w różnych typach trójkątów?
Obliczanie wysokości w trójkątach różni się w zależności od ich rodzaju. W przypadku trójkąta równobocznego, wysokość można łatwo obliczyć, korzystając z prostych wzorów matematycznych, które opierają się na długości boku. Wysokość w trójkącie równobocznym dzieli go na dwa mniejsze trójkąty, co ułatwia obliczenia. Ponadto, wysokość tego trójkąta jest również równa połowie długości boku pomnożonej przez pierwiastek z trzech, co czyni obliczenia prostymi i intuicyjnymi. Dla trójkąta prostokątnego, obliczenie wysokości jest równie proste, ponieważ jedna z wysokości jest jednocześnie długością jednego z boków. Wysokości w tym przypadku można łatwo zidentyfikować, korzystając z definicji trójkąta prostokątnego, gdzie jeden z kątów wynosi 90 stopni. Dzięki temu, wysokości można szybko obliczyć, stosując zasady dotyczące boków trójkąta.trójkąta różnobocznego, sytuacja jest nieco bardziej skomplikowana. Obliczanie wysokości w tym przypadku wymaga znajomości długości wszystkich boków oraz kątów, co czyni je bardziej złożonymi. Można zastosować wzory Herona do obliczenia pola, a następnie wykorzystać je do obliczenia wysokości. Wysokość w trójkącie różnobocznym jest zatem bardziej wyrafinowana i wymaga więcej pracy, ale jest kluczowa dla zrozumienia jego właściwości geometrycznych.
Wysokości w trójkącie równobocznym: prostota obliczeń
Obliczanie wysokości w trójkącie równobocznym jest stosunkowo proste dzięki symetrii tego kształtu. Wysokość trójkąta równobocznego dzieli go na dwa mniejsze trójkąty prostokątne, co pozwala na łatwe obliczenia. Wysokość (h) można obliczyć, korzystając z wzoru: h = (a * √3) / 2, gdzie a to długość boku trójkąta. Na przykład, jeśli bok trójkąta równobocznego ma długość 6 cm, wysokość wynosi h = (6 * √3) / 2 ≈ 5,2 cm. To pokazuje, jak łatwo można określić wysokość w tym typie trójkąta.
| Długość boku (a) [cm] | Wysokość (h) [cm] |
|---|---|
| 4 | 3,46 |
| 5 | 4,33 |
| 6 | 5,20 |
| 7 | 6,06 |
| 8 | 6,93 |
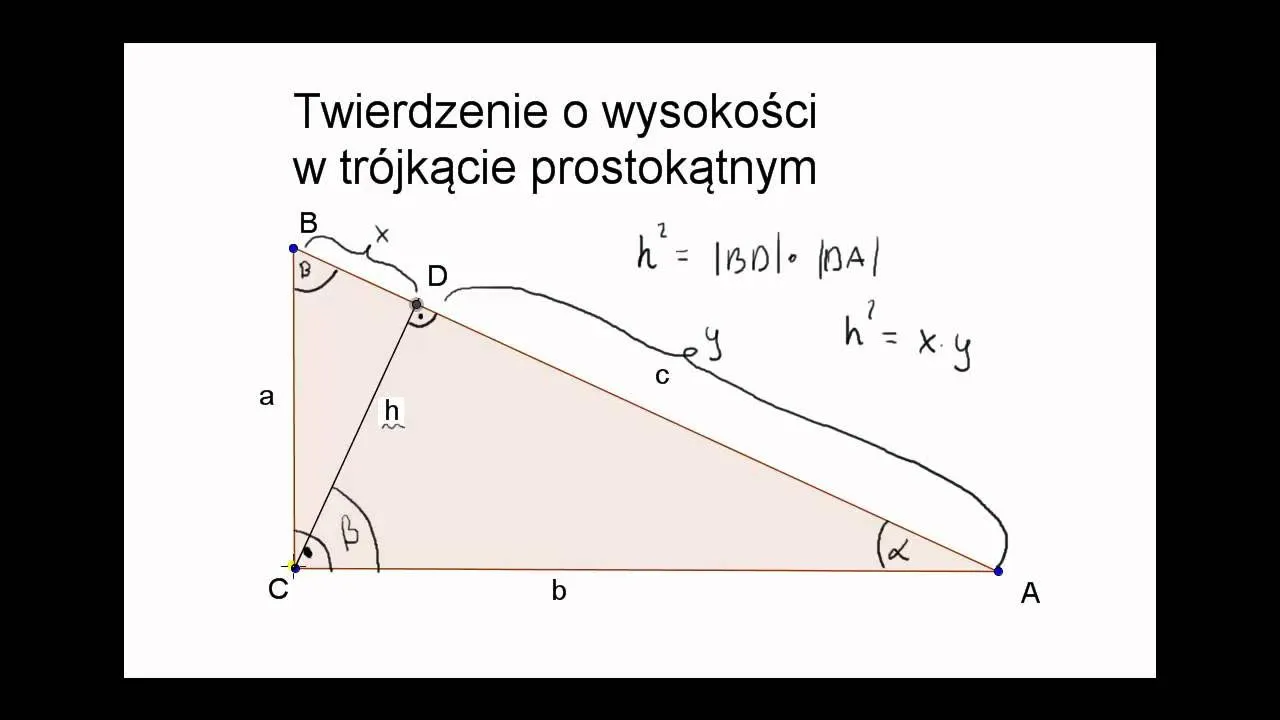
Wysokości w trójkącie prostokątnym: zasady i przykłady
W przypadku trójkąta prostokątnego, obliczanie wysokości jest również proste. Wysokość w tym trójkącie jest równa długości jednego z boków, który jest prostopadły do podstawy. Na przykład, jeśli mamy trójkąt prostokątny o bokach 3 cm i 4 cm, to jego wysokość wzdłuż boku 4 cm wynosi 3 cm. Wysokość można również obliczyć, korzystając z wzoru na pole trójkąta: pole = (podstawa * wysokość) / 2. Jeśli pole wynosi 6 cm², a podstawa to 4 cm, to wysokość wynosi h = (2 * 6) / 4 = 3 cm.
- Trójkąt prostokątny o bokach 3 cm i 4 cm ma wysokość 3 cm wzdłuż boku 4 cm.
- Wysokość w trójkącie prostokątnym można obliczyć jako długość boku prostopadłego do podstawy.
- Obliczając wysokość, można użyć wzoru na pole trójkąta, co ułatwia obliczenia.
Wysokości w trójkącie różnobocznym: wyzwania obliczeniowe
Obliczanie wysokości w trójkącie różnobocznym może być wyzwaniem ze względu na jego nieregularny kształt. W przeciwieństwie do trójkątów równobocznych czy prostokątnych, w których wysokości można łatwo obliczyć z użyciem prostych wzorów, trójkąty różnoboczne wymagają bardziej skomplikowanych metod. Aby obliczyć wysokość, konieczne jest znajomość długości wszystkich boków oraz kątów, co czyni obliczenia bardziej złożonymi. Można zastosować wzór Herona do obliczenia pola trójkąta, a następnie wykorzystać to pole do obliczenia wysokości. Wysokość można obliczyć, korzystając z wzoru: h = (2 * pole) / a, gdzie a to długość podstawy.
Ortocentrum: punkt przecięcia wysokości trójkąta
Ortocentrum to punkt, w którym przecinają się wysokości trójkąta. Jest to istotny element geometrii, ponieważ pozwala zrozumieć, jak różne wysokości współdziałają w trójkącie. Ortocentrum może znajdować się wewnątrz trójkąta, na jego wierzchołku lub na zewnątrz, w zależności od rodzaju trójkąta. W przypadku trójkątów ostrokątnych ortocentrum leży wewnątrz, w trójkątach prostokątnych znajduje się w wierzchołku prostokątnym, a w trójkątach rozwartokątnych jest umiejscowione na zewnątrz.
Znajomość ortocentrum i jego właściwości jest kluczowa dla analizy geometrycznej. To punkt, który łączy różne aspekty trójkąta, a jego znaczenie wykracza poza samą geometrię, mając zastosowanie w różnych dziedzinach, takich jak inżynieria czy architektura. Ortocentrum jest także ważne w kontekście zastosowań praktycznych, gdzie precyzyjne pomiary i obliczenia są kluczowe dla projektów budowlanych i inżynieryjnych.
Znaczenie ortocentrum w geometrii i jego właściwości
Ortocentrum jest punktem, w którym przecinają się wysokości trójkąta. Jego znaczenie w geometrii jest ogromne, ponieważ dostarcza istotnych informacji o kształcie i właściwościach trójkąta. Ortocentrum może znajdować się w różnych miejscach w zależności od rodzaju trójkąta: w trójkącie ostrokątnym leży wewnątrz, w trójkącie prostokątnym w wierzchołku prostokątnym, a w trójkącie rozwartokątnym na zewnątrz. Ta zmienność lokalizacji ortocentrum jest kluczowa dla analizy geometrycznej i pozwala na lepsze zrozumienie relacji między wysokościami a pozostałymi elementami trójkąta.Warto również zauważyć, że ortocentrum jest jednym z punktów charakterystycznych trójkąta, obok centroidu i circumcentru. Każdy z tych punktów ma swoje unikalne właściwości i zastosowania w różnych dziedzinach, takich jak inżynieria czy architektura. Ortocentrum jest istotne nie tylko w kontekście teoretycznym, ale także praktycznym, zwłaszcza w projektowaniu struktur, gdzie precyzyjne obliczenia i zrozumienie właściwości geometrycznych są kluczowe dla stabilności i funkcjonalności budowli.
Praktyczne zastosowania ortocentrum w inżynierii i architekturze
Ortocentrum, jako punkt przecięcia wysokości trójkąta, ma wiele praktycznych zastosowań w inżynierii i architekturze. W projektowaniu budynków, zrozumienie lokalizacji ortocentrum może pomóc inżynierom w określeniu punktów, w których siły działające na konstrukcję będą się równoważyć. Dzięki temu można lepiej rozplanować rozmieszczenie elementów nośnych, co zwiększa stabilność i bezpieczeństwo budowli. Dodatkowo, w przypadku projektów wymagających precyzyjnych obliczeń, takich jak mosty czy wieżowce, ortocentrum może być używane do analizy wpływu obciążeń na różne segmenty konstrukcji.
W przyszłości, z zastosowaniem technologii modelowania informacji o budynku (BIM), inżynierowie będą mogli jeszcze dokładniej analizować ortocentrum w kontekście całej struktury. Dzięki zaawansowanym symulacjom komputerowym, możliwe będzie przewidywanie, jak zmiany w kształcie trójkąta (np. w wyniku obciążeń dynamicznych) mogą wpłynąć na ortocentrum i, w konsekwencji, na stabilność całej konstrukcji. To podejście może zrewolucjonizować sposób, w jaki projektujemy i budujemy, poprawiając zarówno efektywność, jak i bezpieczeństwo budowli.





