W artykule przyjrzymy się różnym rodzajom symetrii, ich właściwościom oraz przykładom, które ilustrują, jak ważna jest ta koncepcja w matematyce. Zrozumienie symetrii nie tylko ułatwia analizę obiektów matematycznych, ale także pozwala na głębsze zrozumienie struktur, które nas otaczają.
Najważniejsze informacje:
- Symetria w matematyce to właściwość obiektów, które pozostają niezmienne podczas przekształceń.
- Rodzaje symetrii obejmują symetrię odbiciową, obrotową i translacyjną.
- Symetria jest obecna w geometrii, algebrze oraz w wielu innych dziedzinach nauki.
- Przykłady symetrii można znaleźć w figurach geometrycznych, takich jak kwadraty i okręgi.
- Wizualizacje, takie jak diagramy, pomagają w zrozumieniu koncepcji symetrii.
Definicja symetrii w matematyce i jej znaczenie w nauce
Symetria w matematyce to fundamentalna właściwość, która odnosi się do figur, brył oraz ogólnie do dowolnych obiektów matematycznych. Oznacza to, że istnieje przekształcenie, które odwzorowuje dany obiekt na niego samego, a brak tej właściwości nazywamy asymetrią. W kontekście matematycznym, symetria jest kluczowa, ponieważ pozwala na zrozumienie i analizowanie struktur, które są niezmienne podczas różnych transformacji.
Znaczenie symetrii wykracza poza samą matematykę, wpływając na różne dziedziny nauki, takie jak fizyka, biologia czy chemia. Dzięki symetrii można lepiej zrozumieć zjawiska naturalne, a także projektować skomplikowane struktury i systemy. W matematyce, symetria jest nie tylko narzędziem analizy, ale również źródłem estetyki i harmonii w różnych dziedzinach, od geometrii po analizę funkcji.
Zrozumienie podstawowych pojęć związanych z symetrią
Aby w pełni zrozumieć, czym jest symetria, warto zapoznać się z podstawowymi pojęciami, które ją definiują. Kluczowe terminy obejmują przekształcenie, które odnosi się do operacji, która zmienia położenie lub kształt obiektu, oraz odwzorowanie, które jest funkcją przypisującą punkty jednego obiektu do punktów drugiego obiektu. Symetria może być również opisana w kontekście grup symetrii, które stanowią zbiór wszystkich przekształceń, które zachowują daną strukturę.
Ważne jest także zrozumienie, że symetria może być lokalna lub globalna. Symetria lokalna dotyczy konkretnych części obiektu, podczas gdy symetria globalna odnosi się do całego obiektu jako całości. Te podstawowe pojęcia stanowią fundament dla dalszych badań i zrozumienia bardziej skomplikowanych typów symetrii.
Rola symetrii w różnych dziedzinach matematyki
Symetria odgrywa istotną rolę w wielu dziedzinach matematyki, w tym w geometrii, algebrze oraz analizie matematycznej. W geometrii, symetria jest kluczowa dla zrozumienia kształtów i ich właściwości, co pozwala na klasyfikację figur według ich symetrii. W algebrze, symetria pomaga w analizie równań i funkcji, umożliwiając zrozumienie ich zachowania.
W analizie matematycznej, symetria jest wykorzystywana do badania zachowania funkcji oraz ich wykresów. Dzięki zrozumieniu symetrii, matematycy mogą przewidywać, jak zmiany w jednym elemencie systemu wpłyną na inne elementy. W ten sposób, symetria staje się nie tylko narzędziem do analizy, ale również sposobem na odkrywanie nowych zjawisk i tworzenie innowacyjnych rozwiązań w matematyce i naukach ścisłych.
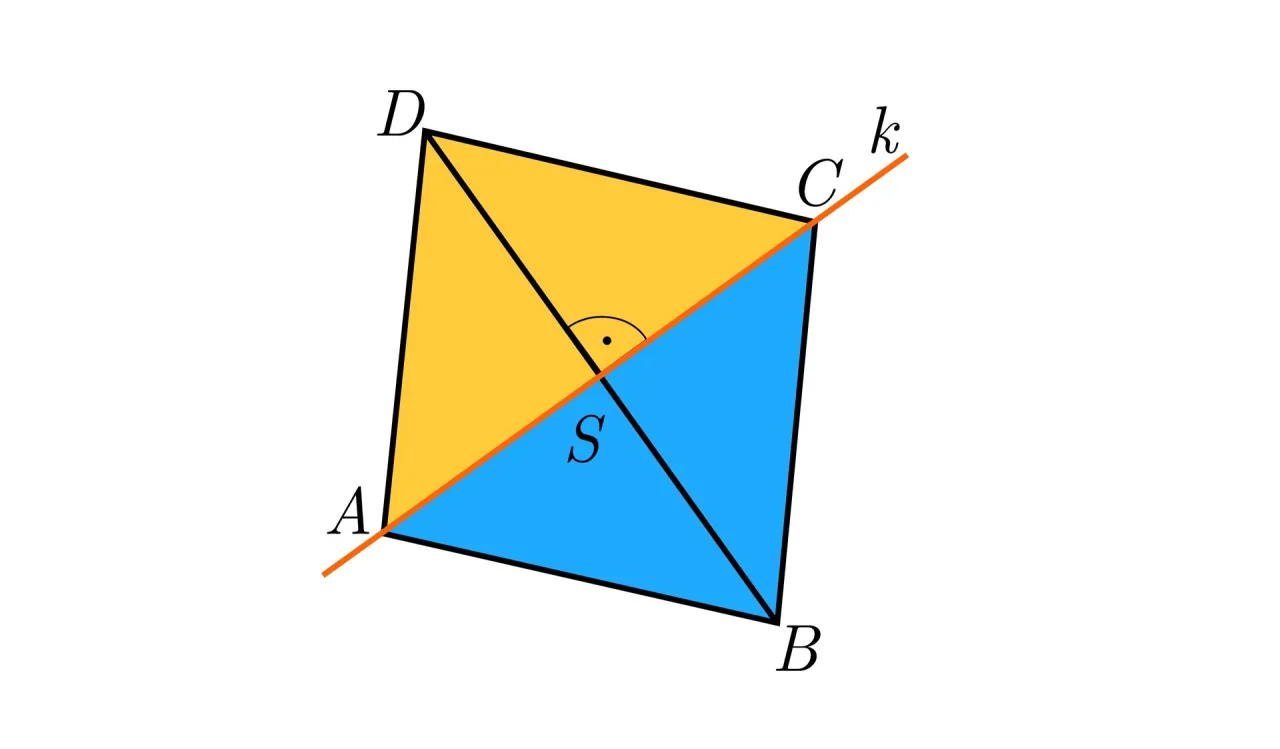
Rodzaje symetrii i ich właściwości w matematyce
W matematyce wyróżniamy różne rodzaje symetrii, które są kluczowe dla zrozumienia właściwości figur i obiektów. Główne typy to symetria odbiciowa, symetria obrotowa oraz symetria translacyjna. Każdy z tych typów ma swoje unikalne cechy i zastosowania, które wpływają na sposób, w jaki analizujemy i interpretujemy różne struktury matematyczne. W tej sekcji przyjrzymy się im bliżej, aby zrozumieć, jak działają i jakie mają właściwości.
Symetria odbiciowa polega na tym, że obiekt może być odzwierciedlony w lustrze, zachowując swoje właściwości. Symetria obrotowa oznacza, że obiekt wygląda tak samo po obrocie wokół określonego punktu. Z kolei symetria translacyjna polega na przesunięciu obiektu w przestrzeni, przy czym jego kształt i rozmiar pozostają niezmienne. Zrozumienie tych rodzajów symetrii jest kluczowe dla dalszej analizy ich zastosowań w matematyce.
Symetria odbiciowa: definicja i przykłady
Symetria odbiciowa, znana również jako symetria lustrzana, to typ symetrii, w którym obiekt jest niezmienny po odbiciu względem linii, zwanej osią symetrii. Przykłady symetrii odbiciowej można znaleźć w przyrodzie, na przykład w ludzkiej twarzy, gdzie lewa i prawa strona są lustrzanym odbiciem siebie. Inny przykład to skrzydła motyla, które są niemal identyczne po obu stronach ciała, co czyni je doskonałym przykładem symetrii odbiciowej.
Właściwości symetrii odbiciowej obejmują nie tylko estetykę, ale także funkcjonalność w biologii i naukach przyrodniczych. Wiele organizmów, takich jak ryby czy ptaki, wykazuje symetrię odbiciową, co wpływa na ich zdolności do poruszania się i przetrwania. Ta forma symetrii jest również wykorzystywana w sztuce i architekturze, gdzie harmonia i równowaga są kluczowe dla kompozycji.
Symetria obrotowa: jak działa i gdzie ją spotkać
Symetria obrotowa to rodzaj symetrii, w której obiekt pozostaje niezmienny po obrocie wokół określonego punktu, zwanym centrum obrotu. Na przykład, gwiazda morska ma symetrię obrotową, ponieważ wygląda tak samo po obrocie o pewien kąt. Innym przykładem są płatki śniegu, które mają sześć ramion, a ich kształt pozostaje niezmienny, gdy są obracane wokół środka.
Właściwości symetrii obrotowej są istotne w wielu dziedzinach, takich jak inżynieria i projektowanie. W inżynierii, zrozumienie symetrii obrotowej pozwala na tworzenie stabilnych struktur, które są bardziej odporne na siły działające w różnych kierunkach. Symetria obrotowa jest także kluczowa w naukach przyrodniczych, gdzie wiele organizmów wykazuje tę formę symetrii, co może wpływać na ich zachowanie i interakcje z otoczeniem.
Symetria translacyjna: zrozumienie i zastosowania
Symetria translacyjna to typ symetrii, w którym obiekt pozostaje niezmienny po przesunięciu w przestrzeni. Oznacza to, że jeśli obiekt jest przesunięty o określoną odległość w jednym kierunku, jego kształt i rozmiar pozostają takie same. Przykłady symetrii translacyjnej można znaleźć w wzornictwie tapet, gdzie powtarzające się motywy tworzą harmonijny i estetyczny efekt wizualny. Inny przykład to tessellacje, czyli pokrycia płaszczyzny figurami, które nie pozostawiają przerw ani nakładających się części.
Właściwości symetrii translacyjnej są istotne w różnych dziedzinach, takich jak sztuka, architektura czy nawet w biologii. Na przykład, wiele organizmów, takich jak niektóre gatunki ryb, wykazuje symetrię translacyjną w swoim wzorze ubarwienia, co może pełnić funkcję kamuflażu. Ponadto, w architekturze, zasady symetrii translacyjnej są wykorzystywane do projektowania budynków, które są zarówno funkcjonalne, jak i estetyczne.
Symetria w algebrze: wpływ na równania i funkcje
Symetria odgrywa ważną rolę w algebrze, wpływając na sposób, w jaki analizujemy równania i funkcje. Funkcje symetryczne są takie, które zachowują swoje właściwości po pewnych przekształceniach, co może ułatwiać ich rozwiązywanie. Na przykład, funkcje parzyste, takie jak f(x) = x², są symetryczne względem osi Y, co oznacza, że f(-x) = f(x). Z kolei funkcje nieparzyste, takie jak f(x) = x³, mają symetrię względem punktu (0,0), co oznacza, że f(-x) = -f(x).
Wykorzystanie symetrii w analizie funkcji pozwala na uproszczenie obliczeń oraz lepsze zrozumienie ich zachowania. Dzięki symetrii można przewidzieć, jak zmiany w jednym elemencie równania wpłyną na inne jego części. Dodatkowo, identyfikacja symetrii w równaniach może prowadzić do szybszego znalezienia miejsc zerowych oraz ekstremów funkcji, co jest kluczowe w wielu zastosowaniach matematycznych.
Przykłady wizualizacji różnych typów symetrii
Wizualizacje są kluczowe dla zrozumienia różnych typów symetrii, ponieważ pomagają w zobrazowaniu koncepcji, które mogą być trudne do uchwycenia tylko w formie tekstowej. Na przykład, symetria odbiciowa może być przedstawiona za pomocą obrazów lustrzanych, które pokazują, jak obiekt wygląda po odbiciu w lustrze. Symetria obrotowa jest często ilustrowana za pomocą diagramów, które pokazują obiekty po obrocie wokół centralnego punktu, co pozwala dostrzec ich powtarzalność. Z kolei symetria translacyjna może być efektywnie wizualizowana poprzez wzory, takie jak te stosowane w tapetach lub tessellacjach, które pokazują, jak obiekty są rozmieszczone w przestrzeni.
| Typ symetrii | Przykład wizualizacji | Opis |
|---|---|---|
| Symetria odbiciowa |  |
Obrazek przedstawiający obiekt i jego lustrzane odbicie. |
| Symetria obrotowa |  |
Diagram ilustrujący obiekt po obrocie o 90 stopni. |
| Symetria translacyjna |  |
Wzór przedstawiający powtarzające się motywy w tessellacji. |
Jak wykorzystać symetrię w sztuce i projektowaniu
Symetria nie tylko odgrywa kluczową rolę w matematyce, ale również ma ogromne znaczenie w sztuce i projektowaniu. Artyści i projektanci często wykorzystują zasady symetrii, aby tworzyć harmonijne i estetyczne kompozycje. Na przykład, w architekturze, budynki zaprojektowane z uwzględnieniem symetrii odbiciowej mogą przyciągać uwagę i wywoływać pozytywne emocje u obserwatorów. Przykłady to klasyczne budowle, takie jak Parlament w Budapeszcie, które zachwycają swoją symetryczną formą.
W przyszłości, technologie projektowania, takie jak programy do modelowania 3D i sztuczna inteligencja, mogą jeszcze bardziej zrewolucjonizować sposób, w jaki wykorzystujemy symetrię. Dzięki tym narzędziom, projektanci będą mogli szybko generować i testować różne symetryczne wzory, co pozwoli na tworzenie bardziej innowacyjnych i złożonych struktur. W miarę jak technologia się rozwija, symetria może stać się kluczowym elementem w tworzeniu zrównoważonych i funkcjonalnych przestrzeni, które odpowiadają na potrzeby współczesnego społeczeństwa.

