W artykule przedstawimy szczegółowe definicje tych funkcji, ich zastosowania oraz wizualizacje, które pomogą lepiej zrozumieć ich działanie. Dzięki zrozumieniu sinusów, cosinusów i tangensów, czytelnicy będą mogli lepiej wykorzystać te pojęcia w różnych dziedzinach, takich jak inżynieria, nauki ścisłe czy codzienne życie.
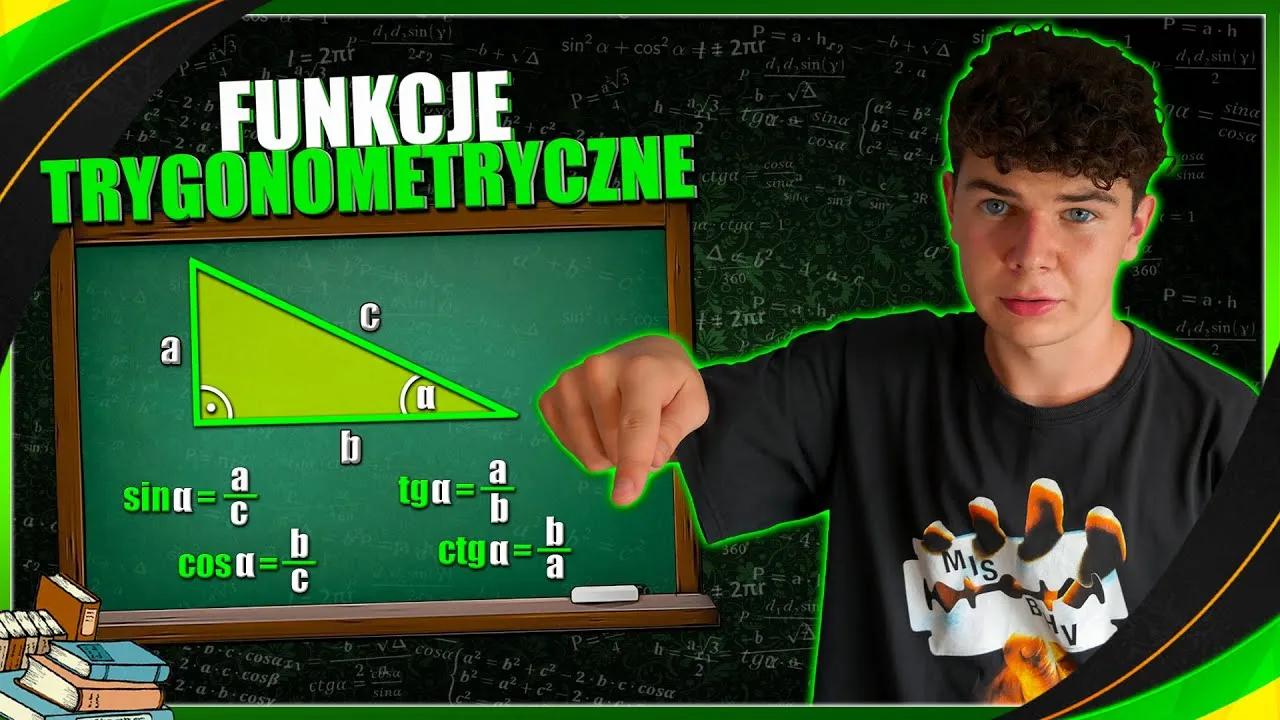
Najważniejsze informacje:- Sinus (sin α) to stosunek długości przeciwprostokątnej do długości przyprostokątnej naprzeciw kąta α.
- Cosinus (cos α) to stosunek długości przeciwprostokątnej do długości przyprostokątnej przyległej do kąta α.
- Tangens (tg α) to stosunek długości przyprostokątnej przeciwległej do kąta α do długości drugiej przyprostokątnej.
- Wizualizacje funkcji trygonometrycznych pomagają w ich lepszym zrozumieniu i zastosowaniu w praktyce.
- Funkcje trygonometryczne są szeroko stosowane w inżynierii, fizyce oraz w codziennych sytuacjach, takich jak nawigacja czy budownictwo.
Definicja sinus, cosinus i tangens: Podstawowe pojęcia matematyczne
Sinus, cosinus i tangens to podstawowe funkcje trygonometryczne, które odgrywają kluczową rolę w matematyce, zwłaszcza w geometrii i trigonometrii. Sinus kąta ostrego α (sin α) definiuje się jako stosunek długości przyprostokątnej leżącej naprzeciw kąta α do długości przeciwprostokątnej. Oznacza to, że jeśli mamy trójkąt prostokątny, sinus kąta α pomoże nam znaleźć relację między tymi dwiema długościami. Cosinus kąta ostrego (cos α) to z kolei stosunek długości przyprostokątnej przyległej do kąta α do długości przeciwprostokątnej. Dzięki temu, cosinus dostarcza informacji o innej relacji w trójkącie prostokątnym.
Na koniec, tangens kąta ostrego α (tg α) definiuje się jako stosunek długości przyprostokątnej przeciwległej do kąta α do długości drugiej przyprostokątnej. Tangens jest szczególnie przydatny, gdy chcemy obliczyć wysokość obiektów lub odległości w sytuacjach, gdy nie możemy bezpośrednio zmierzyć tych wartości. Wszystkie te funkcje są ze sobą powiązane i stanowią fundament dla wielu bardziej złożonych zagadnień matematycznych oraz zastosowań praktycznych.
Sinus: Zrozumienie funkcji i jej zastosowań w geometrii
Sinus jest jedną z podstawowych funkcji trygonometrycznych, która odgrywa ważną rolę w analizie kątów w trójkątach prostokątnych. Wartość sin α można obliczyć, dzieląc długość boku naprzeciw kąta α przez długość przeciwprostokątnej. Na przykład, w trójkącie prostokątnym o kącie α równym 30 stopni, sinus wynosi 0,5, co oznacza, że długość boku naprzeciw kąta α wynosi połowę długości przeciwprostokątnej.
W geometrii, sinus jest używany do obliczania wysokości trójkątów oraz w wielu zastosowaniach praktycznych, takich jak obliczenia związane z falami dźwiękowymi czy światłem. Dzięki funkcji sinus możemy także modelować zjawiska cykliczne, co znajduje zastosowanie w inżynierii i naukach przyrodniczych.
Cosinus: Kluczowe aspekty i znaczenie w trigonometrii
Cosinus kąta ostrego α (cos α) to jedna z podstawowych funkcji trygonometrycznych, która odgrywa istotną rolę w matematyce. Cosinus definiuje się jako stosunek długości przyprostokątnej przyległej do kąta α do długości przeciwprostokątnej. Na przykład, w trójkącie prostokątnym, jeśli mamy kąt α równy 60 stopni, cos α wynosi 0,5, co oznacza, że długość boku przyległego do kąta α stanowi połowę długości przeciwprostokątnej. Ta relacja jest niezwykle ważna w różnych obliczeniach geometrycznych.
W trigonometrii, cosinus jest używany do obliczania wartości kątów oraz długości boków w trójkątach. Zastosowanie cosinusa jest szerokie, obejmując wiele dziedzin, takich jak inżynieria, architektura czy fizyka. Dzięki funkcji cosinus możemy również analizować zjawiska cykliczne, takie jak fale dźwiękowe czy świetlne, co czyni ją niezwykle przydatną w naukach przyrodniczych.
Tangens: Jak wykorzystać tę funkcję w praktyce
Tangens kąta ostrego α (tg α) to kolejna funkcja trygonometryczna, która jest definiowana jako stosunek długości przyprostokątnej przeciwległej do kąta α do długości przyprostokątnej przyległej do tego kąta. Obliczamy tangens, dzieląc długość boku przeciwległego przez długość boku przyległego. Na przykład, w trójkącie prostokątnym o kącie α równym 45 stopni, tg α wynosi 1, co oznacza, że długości boków przeciwległego i przyległego są równe.
W praktyce, tangens jest niezwykle przydatny w różnych zastosowaniach, takich jak obliczenia wysokości obiektów, odległości w geodezji, czy nawet w architekturze. Funkcja ta pozwala na łatwe przekształcanie pomiarów kątowych na konkretne wartości długości, co jest nieocenione w wielu dziedzinach. Warto jednak pamiętać, że przy obliczaniu wartości tangensa, łatwo popełnić błędy, zwłaszcza przy kątach bliskich 90 stopni, gdzie tangens staje się nieskończony.
Wizualizacja funkcji: Diagramy i wykresy dla lepszego zrozumienia
Wizualizacja funkcji trygonometrycznych, takich jak sinus, cosinus i tangens, jest kluczowym elementem w nauce o tych pojęciach. Diagramy i wykresy pozwalają na lepsze zrozumienie, jak te funkcje działają oraz jak zmieniają się w zależności od wartości kątów. Dzięki graficznym reprezentacjom, uczniowie oraz profesjonaliści mogą łatwiej dostrzegać wzorce i relacje między różnymi funkcjami. Wizualizacje są szczególnie przydatne w kontekście zjawisk cyklicznych, które są często związane z tymi funkcjami, na przykład w analizie fal dźwiękowych i elektromagnetycznych.
Wykresy funkcji trygonometrycznych pomagają również w rozwiązywaniu problemów matematycznych, umożliwiając wizualne przedstawienie zjawisk, które w przeciwnym razie mogłyby być trudne do zrozumienia. Umożliwiają one także identyfikację kluczowych punktów, takich jak maksima, minima oraz punkty przecięcia z osią X, co jest nieocenione w wielu zastosowaniach praktycznych.
Jak interpretować wykresy sinusoidy, cosinusa i tangensa
Interpretacja wykresów funkcji sinus, cosinus i tangens wymaga zrozumienia ich kluczowych cech. Wykres sinusoidy jest falowy i oscyluje między wartościami -1 a 1, z określonym okresem. Amplituda fali sinusoidalnej pokazuje, jak daleko od osi X wznosi się i opada. Z kolei wykres cosinusa jest podobny do wykresu sinusa, ale przesunięty w lewo o 90 stopni, co oznacza, że jego maksimum występuje przy kącie 0 stopni. Wykres tangensa ma zupełnie inną strukturę, z wartościami rosnącymi do nieskończoności w punktach, gdzie funkcja jest niezdefiniowana, co prowadzi do tzw. asymptot w określonych miejscach.- Wykres sin α ma okres równy 360 stopni (2π radianów) i oscyluje między -1 a 1.
- Wykres cos α również ma okres 360 stopni, ale osiąga maksimum przy 0 stopniach.
- Wykres tg α ma okres 180 stopni (π radianów) i nie ma ograniczeń, co prowadzi do asymptot.
| Funkcja | Okres | Amplituda | Zakres |
| Sinus | 360 stopni | 1 | -1 do 1 |
| Cosinus | 360 stopni | 1 | -1 do 1 |
| Tangens | 180 stopni | Brak (nieskończoność) | Całe liczby rzeczywiste |
Przykłady zastosowań wykresów w rozwiązywaniu problemów
Wykresy funkcji sinus, cosinus i tangens są niezwykle przydatne w rozwiązywaniu różnych problemów matematycznych. Na przykład, można wykorzystać wykres sinusoidy do określenia wartości sin α dla konkretnego kąta, co jest pomocne w obliczeniach związanych z falami akustycznymi. W przypadku wykresu cosinusa, można łatwo znaleźć wartości cos α, co jest przydatne przy projektowaniu budynków, aby zapewnić odpowiednie kąty nachylenia dachów. Z kolei wykres tangensa może być użyty do obliczenia wysokości obiektów, takich jak wieże czy budynki, poprzez pomiar kątów widzenia z określonej odległości.
Przykładowo, jeśli chcemy obliczyć wysokość budynku, możemy użyć tangensa kąta, pod jakim obserwujemy szczyt budynku. Korzystając z wykresu tangensa, możemy szybko znaleźć wartość tg α, a następnie użyć tej wartości do obliczenia wysokości budynku na podstawie znanej odległości od niego. Takie zastosowania wykresów funkcji trygonometrycznych są nieocenione w praktyce, ponieważ pozwalają na szybkie i efektywne rozwiązywanie problemów.
Czytaj więcej: Jak się liczy skalę w matematyce? Proste przykłady i wyjaśnienia
Zastosowania praktyczne: Gdzie sinus, cosinus i tangens są używane?
Funkcje sinus, cosinus i tangens mają szerokie zastosowanie w różnych dziedzinach życia oraz nauki. W inżynierii, są one wykorzystywane do obliczania kątów i długości w projektach budowlanych, takich jak konstrukcja mostów czy budynków. W fizyce, funkcje te pomagają w opisie zjawisk falowych, takich jak dźwięk czy światło. Oprócz tego, w nawigacji, sinus i cosinus są używane do obliczania pozycji statków i samolotów na podstawie kątów oraz odległości.
W codziennym życiu, funkcje trygonometryczne mogą być stosowane w takich sytuacjach jak obliczanie kątów w projektach DIY, planowanie przestrzeni w ogrodach, czy nawet w sporcie, gdzie precyzyjne obliczenia kątów mogą wpłynąć na technikę wykonywania ruchów. Dzięki tym zastosowaniom, zrozumienie pojęć takich jak sinus, cosinus i tangens staje się nie tylko teoretyczne, ale również praktyczne, co czyni je istotnymi w wielu aspektach życia.
Trigonometryczne zastosowania w inżynierii i naukach ścisłych
Funkcje trygonometryczne, takie jak sinus, cosinus i tangens, mają kluczowe znaczenie w inżynierii i naukach ścisłych. W inżynierii mechanicznej, te funkcje są używane do analizy sił działających na obiekty, co pozwala inżynierom na projektowanie stabilnych konstrukcji. Na przykład, w obliczeniach związanych z mostami, sinus i cosinus pomagają w określeniu kątów nachylenia oraz sił działających na poszczególne elementy konstrukcji. W elektrotechnice, funkcje te są niezbędne do analizy obwodów prądu zmiennego, gdzie sinusoidalne przebiegi napięcia i prądu są standardem.
W geodezji, funkcje trygonometryczne są stosowane do określania wysokości i odległości w terenie. Na przykład, przy pomocy tangensa można obliczyć wysokość góry, znając kąt widzenia oraz odległość od jej podstawy. W naukach przyrodniczych, takich jak fizyka, funkcje te są używane do opisu ruchu falowego i drgań, co jest fundamentalne w badaniach akustycznych i optycznych. Te zastosowania pokazują, jak ważne są sinus, cosinus i tangens w różnych dziedzinach inżynieryjnych i naukowych.
- Inżynieria mechaniczna - analiza sił i kątów w konstrukcjach.
- Elektrotechnika - analiza obwodów prądu zmiennego z użyciem funkcji sinusoidalnych.
- Geodezja - obliczanie wysokości i odległości w terenie z użyciem tangensa.
- Nauki przyrodnicze - opis ruchu falowego i drgań w akustyce i optyce.
Sinus, cosinus i tangens w codziennym życiu: Przykłady i sytuacje
Funkcje trygonometryczne, takie jak sinus, cosinus i tangens, znajdują zastosowanie w wielu codziennych sytuacjach, które mogą być zaskakujące. Na przykład, w budownictwie, przy planowaniu dachów, inżynierowie używają tych funkcji do obliczania kątów nachylenia, co wpływa na efektywność odprowadzania wody. W nawigacji, zarówno morskiej, jak i lotniczej, sinus i cosinus są wykorzystywane do obliczania kursów i pozycji na mapach, co jest kluczowe dla bezpieczeństwa podróży.
W sporcie, funkcje te pomagają w analizie ruchu zawodników, na przykład w gimnastyce, gdzie precyzyjne obliczenia kątów mogą wpłynąć na wykonanie skoków i akrobacji. Nawet w codziennym życiu, podczas planowania ogrodu, można wykorzystać tangens do określenia odpowiednich kątów dla nasadzeń, aby zapewnić optymalne nasłonecznienie. Te przykłady pokazują, jak funkcje trygonometryczne są integralną częścią naszego codziennego funkcjonowania.
Nowe technologie w zastosowaniach funkcji trygonometrycznych
W miarę jak technologia się rozwija, funkcje trygonometryczne znajdują nowe zastosowania w zaawansowanych dziedzinach, takich jak analiza danych czy sztuczna inteligencja. Na przykład, w kontekście analizy danych, sinus i cosinus mogą być używane do modelowania zjawisk cyklicznych w zbiorach danych, co pozwala na przewidywanie trendów w czasie. Dzięki zastosowaniu algorytmów uczenia maszynowego, funkcje trygonometryczne mogą być wykorzystywane do analizy danych z czujników w czasie rzeczywistym, co jest kluczowe w systemach monitorowania i automatyzacji.Dodatkowo, w obszarze rzeczywistości rozszerzonej (AR) i rzeczywistości wirtualnej (VR), funkcje sinusoidalne odgrywają istotną rolę w symulacji ruchu i interakcji w wirtualnych środowiskach. Poprzez precyzyjne obliczenia kątów i odległości, twórcy gier i aplikacji mogą stworzyć bardziej realistyczne doświadczenia dla użytkowników. W przyszłości możemy spodziewać się jeszcze większego połączenia funkcji trygonometrycznych z technologią, co otworzy nowe możliwości w różnych branżach, od medycyny po rozrywkę.





