Pierwiastek w matematyce to fundamentalne pojęcie, które odgrywa kluczową rolę w wielu dziedzinach matematyki i nauk ścisłych. W najprostszych słowach, pierwiastek to liczba, która, podniesiona do określonej potęgi, daje inną liczbę. Najczęściej spotykanym rodzajem pierwiastka jest pierwiastek kwadratowy, który oznaczamy symbolem $$\sqrt{}$$. Na przykład, pierwiastek kwadratowy z liczby 16 to 4, ponieważ $$4^2 = 16$$. Istnieją również pierwiastki sześcienne oraz pierwiastki wyższych stopni, które są istotne w rozwiązywaniu równań i modelowaniu zjawisk w różnych dziedzinach nauki.
W artykule przyjrzymy się bliżej definicji pierwiastków, ich rodzajom oraz praktycznym zastosowaniom. Zrozumienie tych pojęć jest nie tylko ważne dla uczniów i studentów, ale także dla każdego, kto chce lepiej poznać matematykę i jej zastosowania w życiu codziennym.
Kluczowe wnioski:
- Pierwiastek to liczba, która, podniesiona do określonej potęgi, daje inną liczbę.
- Najczęściej spotykanym pierwiastkiem jest pierwiastek kwadratowy, oznaczany symbolem $$\sqrt{}$$.
- Pierwiastek sześcienny to liczba, która podniesiona do potęgi trzeciej daje określoną wartość.
- Pierwiastki są kluczowe w rozwiązywaniu równań, szczególnie równań kwadratowych.
- Pierwiastki mają zastosowanie w wielu dziedzinach, takich jak fizyka, inżynieria i ekonomia.
Co to jest pierwiastek w matematyce i jego definicja?
Pierwiastek w matematyce to liczba, która, podniesiona do określonej potęgi, daje inną liczbę. To działanie odwrotne do potęgowania, co oznacza, że pierwiastek pozwala nam znaleźć wartość, która, pomnożona przez siebie, daje określony wynik. Najczęściej spotykanym typem pierwiastka jest pierwiastek kwadratowy, oznaczany symbolem $$\sqrt{}$$. Na przykład, pierwiastek kwadratowy z liczby 16 to 4, ponieważ $$4^2 = 16$$. Wynikiem pierwiastkowania jest zawsze liczba nieujemna, co oznacza, że pod pierwiastkiem może stać tylko liczba nieujemna.
Warto zauważyć, że istnieją także inne rodzaje pierwiastków, takie jak pierwiastek sześcienny, który jest pierwiastkiem trzeciego stopnia. Pierwiastki są kluczowe w rozwiązywaniu równań matematycznych, szczególnie równań kwadratowych, gdzie pomagają określić miejsca zerowe funkcji. W praktyce, pierwiastki znajdują zastosowanie w różnych dziedzinach nauki, takich jak fizyka, inżynieria czy ekonomia, gdzie są wykorzystywane do obliczeń geometrycznych i analizy danych.
Zrozumienie podstawowych pojęć związanych z pierwiastkami
Pierwiastki są fundamentalnym pojęciem w matematyce, które łączy się z pojęciem potęgowania. Pierwiastek kwadratowy to liczba, która, podniesiona do drugiej potęgi, daje określoną wartość. Na przykład, $$\sqrt{25}$$ to 5, ponieważ $$5^2 = 25$$. Z kolei pierwiastek sześcienny to liczba, która, podniesiona do trzeciej potęgi, daje określoną wartość, jak w przypadku $$\sqrt[3]{8}$$, co równa się 2, ponieważ $$2^3 = 8$$.
W matematyce, pierwiastki są używane do rozwiązywania równań oraz w obliczeniach dotyczących różnych zjawisk. Zrozumienie tych podstawowych pojęć jest kluczowe dla dalszego zgłębiania tematów związanych z pierwiastkami, ich rodzajami i zastosowaniami. Ogólnie rzecz biorąc, pierwiastki stanowią ważny element matematyki, który ma szerokie zastosowanie w wielu dziedzinach.
Różnice między pierwiastkiem kwadratowym a sześciennym
Pierwiastki kwadratowe i sześcienne to dwa podstawowe typy pierwiastków w matematyce, które różnią się zarówno definicjami, jak i właściwościami. Pierwiastek kwadratowy to liczba, która, podniesiona do drugiej potęgi, daje zadaną wartość. Na przykład, $$\sqrt{9}$$ wynosi 3, ponieważ $$3^2 = 9$$. Z kolei pierwiastek sześcienny to liczba, która, podniesiona do trzeciej potęgi, również daje określoną wartość, jak w przypadku $$\sqrt[3]{27}$$, co równa się 3, ponieważ $$3^3 = 27$$.
Ważne jest, aby zrozumieć, że pierwiastki kwadratowe są używane głównie w kontekście liczb nieujemnych, podczas gdy pierwiastki sześcienne mogą być stosowane zarówno dla liczb dodatnich, jak i ujemnych. To sprawia, że pierwiastki sześcienne są bardziej uniwersalne w zastosowaniach. Poniższa tabela ilustruje kluczowe różnice między tymi dwoma typami pierwiastków, w tym ich definicje oraz przykłady wartości.
| Typ pierwiastka | Definicja | Przykład | Wynik |
| Pierwiastek kwadratowy | Liczba, która podniesiona do drugiej potęgi daje określoną wartość | $$\sqrt{16}$$ | 4 |
| Pierwiastek sześcienny | Liczba, która podniesiona do trzeciej potęgi daje określoną wartość | $$\sqrt[3]{27}$$ | 3 |
Rodzaje pierwiastków i ich charakterystyka
W matematyce wyróżniamy różne rodzaje pierwiastków, z których dwa najczęściej spotykane to pierwiastek kwadratowy i pierwiastek sześcienny. Oba typy mają swoje unikalne definicje oraz właściwości, które są kluczowe dla ich zrozumienia. Pierwiastek kwadratowy, oznaczany symbolem $$\sqrt{}$$, jest pierwiastkiem drugiego stopnia, co oznacza, że jego wartość to liczba, która, podniesiona do drugiej potęgi, daje daną liczbę. Z kolei pierwiastek sześcienny, również oznaczany symbolem $$\sqrt{}$$, jest pierwiastkiem trzeciego stopnia, co oznacza, że jego wartość to liczba, która, podniesiona do trzeciej potęgi, daje określoną wartość.
Pierwiastek kwadratowy jest stosowany głównie w kontekście liczb nieujemnych, a jego wynik zawsze będzie liczbą nieujemną. Na przykład, pierwiastek kwadratowy z liczby 25 to 5, ponieważ $$5^2 = 25$$. Z kolei pierwiastek sześcienny może być zarówno dodatni, jak i ujemny, co czyni go bardziej uniwersalnym. Na przykład, pierwiastek sześcienny z liczby -8 to -2, ponieważ $$(-2)^3 = -8$$. Zrozumienie tych dwóch typów pierwiastków jest kluczowe dla dalszego zgłębiania zagadnień matematycznych.
Pierwiastek kwadratowy – definicja i przykłady
Pierwiastek kwadratowy to liczba, która, podniesiona do drugiej potęgi, daje określoną wartość. Oznaczany jest symbolem $$\sqrt{}$$. Na przykład, $$\sqrt{16}$$ wynosi 4, ponieważ $$4^2 = 16$$. Wynikiem pierwiastkowania jest zawsze liczba nieujemna, co oznacza, że pierwiastek kwadratowy z liczby nieujemnej $$a$$ to taka liczba $$b$$, której kwadrat jest równy $$a$$. Wartością pierwiastka kwadratowego z liczby 0 jest 0, a pierwiastek kwadratowy z liczby ujemnej nie jest liczbą rzeczywistą.
- $$\sqrt{1} = 1$$
- $$\sqrt{4} = 2$$
- $$\sqrt{9} = 3$$
- $$\sqrt{16} = 4$$
- $$\sqrt{25} = 5$$
Pierwiastek sześcienny – definicja i zastosowania
Pierwiastek sześcienny to liczba, która, podniesiona do potęgi trzeciej, daje określoną wartość. Oznaczany jest symbolem $$\sqrt[3]{}$$. Na przykład, pierwiastek sześcienny z liczby 27 wynosi 3, ponieważ $$3^3 = 27$$. Wartością pierwiastka sześciennego z liczby -8 jest -2, ponieważ $$(-2)^3 = -8$$. To sprawia, że pierwiastki sześcienne mogą być zarówno dodatnie, jak i ujemne, co czyni je bardziej uniwersalnymi niż pierwiastki kwadratowe.
Pierwiastki sześcienne mają wiele zastosowań w różnych dziedzinach. Na przykład, w geometrii używa się ich do obliczania objętości sześcianów. Jeśli mamy sześcian o objętości 64 jednostek sześciennych, możemy obliczyć długość krawędzi, biorąc pierwiastek sześcienny z tej objętości: $$\sqrt[3]{64} = 4$$, co oznacza, że długość każdej krawędzi sześcianu wynosi 4 jednostki. Takie zastosowania są istotne w inżynierii oraz architekturze, gdzie precyzyjne obliczenia objętości są kluczowe.
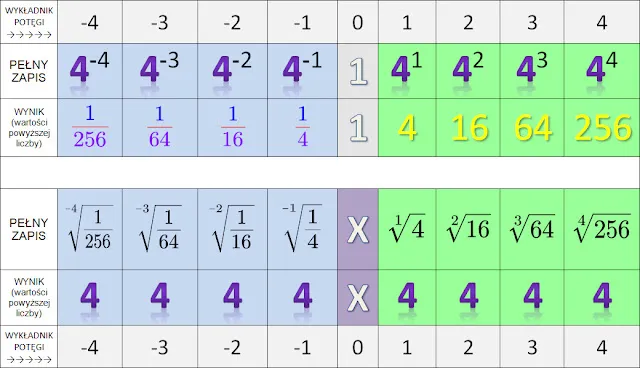
Praktyczne zastosowania pierwiastków w matematyce
Pierwiastki mają istotne znaczenie w rozwiązywaniu równań matematycznych, zwłaszcza w kontekście równań kwadratowych. W takich równaniach, pierwiastki są używane do określenia miejsc zerowych funkcji. Na przykład, w równaniu kwadratowym postaci $$ax^2 + bx + c = 0$$, aby znaleźć wartości $$x$$, które spełniają to równanie, można skorzystać z wzoru kwadratowego, który wykorzystuje pierwiastki. Wzór ten ma postać $$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$, gdzie pierwiastek kwadratowy odgrywa kluczową rolę w obliczaniu wartości funkcji.
Pierwiastki są również szeroko stosowane w naukach ścisłych i inżynierii. Na przykład, w fizyce pierwiastki sześcienne są wykorzystywane do obliczania objętości brył, takich jak sześciany czy prostopadłościany. W inżynierii, pierwiastki pomagają w analizie danych oraz modelowaniu zjawisk, takich jak przepływ cieczy czy obliczenia związane z materiałami budowlanymi. W każdej z tych dziedzin, umiejętność obliczania pierwiastków jest niezbędna do dokładnych i efektywnych rozwiązań.
Jak pierwiastki pomagają w rozwiązywaniu równań?
Pierwiastki są kluczowe w rozwiązywaniu równań, szczególnie tych kwadratowych. Na przykład, aby rozwiązać równanie $$x^2 - 9 = 0$$, można przekształcić je do postaci $$x^2 = 9$$. Następnie, biorąc pierwiastek kwadratowy z obu stron, otrzymujemy $$x = \pm 3$$. To pokazuje, jak pierwiastki pozwalają znaleźć rozwiązania równań, co jest fundamentalne w matematyce.
Zastosowanie pierwiastków w naukach ścisłych i inżynierii
Pierwiastki mają wiele zastosowań w różnych dziedzinach nauki i inżynierii. Na przykład, w fizyce pierwiastek sześcienny jest używany do obliczania objętości sześcianów i innych brył. W inżynierii, pierwiastki są istotne w analizie strukturalnej, gdzie obliczenia objętości materiałów są kluczowe dla projektowania. Dodatkowo, w statystyce pierwiastki są używane do obliczania odchyleń standardowych, co jest istotne w analizie danych.
- Obliczanie objętości sześcianów w inżynierii budowlanej.
- Analiza danych statystycznych przy użyciu pierwiastków do obliczania odchyleń standardowych.
- Obliczenia w fizyce związane z przepływem cieczy i ich objętościami.
Nowoczesne techniki obliczania pierwiastków w praktyce
W miarę jak technologia się rozwija, pojawiają się nowoczesne techniki obliczania pierwiastków, które mogą znacznie ułatwić pracę w matematyce, inżynierii i naukach ścisłych. Jednym z takich podejść jest wykorzystanie algorytmów komputerowych do szybkiego i precyzyjnego obliczania pierwiastków, co jest szczególnie przydatne w przypadku dużych zbiorów danych lub bardziej złożonych równań. Dzięki technologiom takim jak uczenie maszynowe, można stworzyć modele, które przewidują wartości pierwiastków na podstawie wcześniejszych danych, co oszczędza czas i zwiększa dokładność obliczeń.
Dodatkowo, aplikacje mobilne i oprogramowanie matematyczne, takie jak Wolfram Alpha czy GeoGebra, oferują funkcje, które umożliwiają użytkownikom łatwe obliczanie pierwiastków i wizualizację wyników. Te narzędzia nie tylko przyspieszają proces obliczeń, ale także pomagają w lepszym zrozumieniu koncepcji matematycznych, co jest szczególnie cenne dla studentów i profesjonalistów. W przyszłości można oczekiwać dalszego rozwoju takich technologii, co z pewnością wpłynie na sposób, w jaki uczymy się i stosujemy pierwiastki w matematyce.

