Pole trójkąta to kluczowy element geometrii, który można obliczyć na kilka sposobów. Najpopularniejszym z nich jest wzór oparty na długości podstawy i wysokości, który pozwala na szybkie i efektywne obliczenie powierzchni tego kształtu. Warto znać również inne metody, takie jak wzór Herona, który umożliwia obliczenie pola na podstawie długości wszystkich boków trójkąta.
W artykule przyjrzymy się różnym typom trójkątów, takim jak trójkąty równoboczne, równoramienne i prostokątne, a także ich specyficznym właściwościom wpływającym na obliczenia. Zrozumienie tych metod pomoże w praktycznym zastosowaniu wiedzy o polu trójkąta w codziennym życiu, na przykład w architekturze czy przy planowaniu przestrzeni. Zapraszamy do zapoznania się z naszym przewodnikiem po skutecznych metodach obliczania pola trójkąta.
Najważniejsze informacje:- Podstawowy wzór na pole trójkąta to \( P = \frac{1}{2} \cdot a \cdot h \).
- Wzór Herona pozwala obliczyć pole trójkąta na podstawie długości wszystkich trzech boków.
- Trójkąty dzielimy na różne typy, w tym równoboczne, równoramienne i prostokątne, z unikalnymi wzorami dla każdego z nich.
- Trójkąt równoboczny ma wzór \( P = \frac{a^2 \cdot \sqrt{3}}{4} \), gdzie \( a \) to długość boku.
- Trójkąt prostokątny można obliczyć za pomocą wzoru \( P = \frac{1}{2} \cdot a \cdot b \), gdzie \( a \) i \( b \) to długości boków tworzących kąt prosty.
Jak obliczyć pole trójkąta w prosty sposób i skutecznie
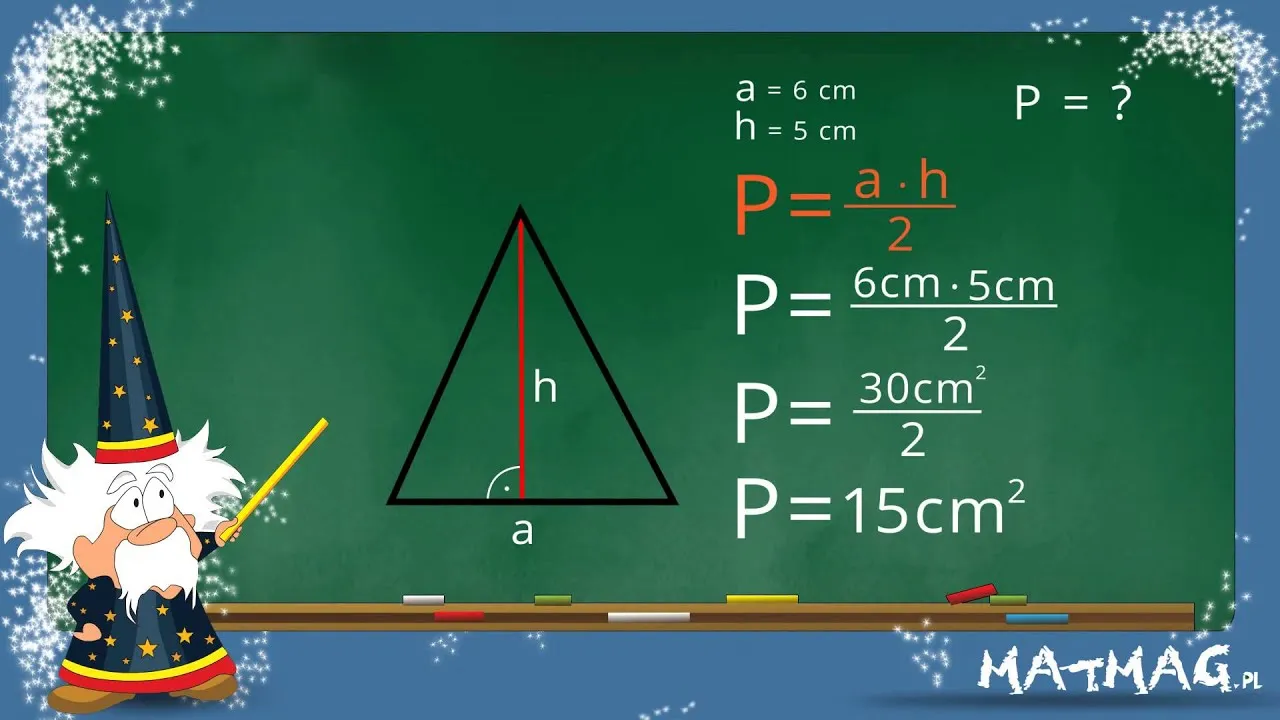
Aby obliczyć pole trójkąta, najczęściej wykorzystujemy wzór oparty na podstawie i wysokości. Podstawowy wzór to P = \frac{1}{2} \cdot a \cdot h, gdzie a to długość podstawy, a h to wysokość trójkąta opuszczona na tę podstawę. Dzięki temu prostemu wzorowi możemy szybko uzyskać wynik, co czyni go najpopularniejszą metodą obliczania pola trójkąta.
W praktyce, aby skorzystać z tego wzoru, musimy znać długość podstawy oraz wysokość. Na przykład, jeśli mamy trójkąt o podstawie 10 cm i wysokości 5 cm, obliczamy pole w następujący sposób: P = \frac{1}{2} \cdot 10 \cdot 5 = 25 cm². To oznacza, że pole tego trójkąta wynosi 25 centymetrów kwadratowych. Metoda ta jest niezwykle prosta i efektywna, co czyni ją idealnym rozwiązaniem dla uczniów oraz osób zajmujących się geometrią.
Wzór na pole trójkąta: podstawy i wysokość w praktyce
Wzór na pole trójkąta, czyli P = \frac{1}{2} \cdot a \cdot h, jest kluczowy w geometrii. Dzięki niemu możemy szybko i skutecznie obliczyć powierzchnię trójkąta, znając jedynie długość jego podstawy oraz wysokości. Wysokość jest mierzona prostopadle do podstawy, co jest istotne dla poprawności obliczeń.Na przykład, rozważmy trójkąt, którego podstawa wynosi 8 cm, a wysokość 4 cm. Aby obliczyć pole, stosujemy wzór: P = \frac{1}{2} \cdot 8 \cdot 4 = 16 cm². To oznacza, że pole tego trójkąta wynosi 16 centymetrów kwadratowych. Takie obliczenia są nie tylko proste, ale także niezwykle przydatne w wielu dziedzinach, takich jak architektura czy inżynieria.
Wzór Herona: obliczanie pola na podstawie boków trójkąta
Wzór Herona to doskonała metoda obliczania pola trójkąta, gdy znamy długości wszystkich trzech boków. Wzór ten jest szczególnie przydatny, gdy nie mamy wysokości trójkąta, a jedynie długości jego boków. Aby skorzystać z tego wzoru, najpierw obliczamy półobwód trójkąta, korzystając z formuły: s = \frac{a + b + c}{2}, gdzie a, b i c to długości boków trójkąta.
Po obliczeniu półobwodu możemy użyć wzoru Herona do obliczenia pola: P = \sqrt{s \cdot (s - a) \cdot (s - b) \cdot (s - c)}. Na przykład, jeśli mamy trójkąt o bokach długości 5 cm, 6 cm i 7 cm, najpierw obliczamy półobwód: s = \frac{5 + 6 + 7}{2} = 9 cm. Następnie obliczamy pole: P = \sqrt{9 \cdot (9 - 5) \cdot (9 - 6) \cdot (9 - 7)} = \sqrt{9 \cdot 4 \cdot 3 \cdot 2} = \sqrt{216} \approx 14.7 cm². To oznacza, że pole tego trójkąta wynosi około 14.7 centymetrów kwadratowych.
Różne typy trójkątów i ich specyfika w obliczeniach
Trójkąty dzielimy na kilka typów, z których każdy ma swoje unikalne właściwości wpływające na sposób obliczania pola trójkąta. Do najważniejszych typów należą trójkąty równoboczne, równoramienne oraz prostokątne. Każdy z tych typów różni się długością boków oraz kątami, co ma bezpośredni wpływ na obliczenia.
Trójkąty równoboczne mają wszystkie boki równej długości, co pozwala na użycie specjalnych wzorów do obliczania pola. Trójkąty równoramienne mają dwa boki tej samej długości, a ich wysokość można łatwo obliczyć. Natomiast w trójkątach prostokątnych jedna z kątów wynosi 90 stopni, co umożliwia zastosowanie prostych wzorów bazujących na podstawie i wysokości. Zrozumienie tych różnic jest kluczowe dla skutecznego obliczania pola różnych typów trójkątów.
Trójkąt równoboczny: unikalne podejście do obliczania pola
Trójkąt równoboczny to szczególny przypadek trójkąta, w którym wszystkie boki mają tę samą długość. Aby obliczyć jego pole, stosujemy wzór: P = \frac{a^2 \cdot \sqrt{3}}{4}, gdzie a to długość boku trójkąta. Ten wzór wynika z właściwości równobocznych boków oraz kątów, co sprawia, że obliczenia są znacznie prostsze w porównaniu do innych typów trójkątów.
Na przykład, jeśli mamy trójkąt równoboczny o boku długości 6 cm, obliczamy pole w następujący sposób: P = \frac{6^2 \cdot \sqrt{3}}{4} = \frac{36 \cdot \sqrt{3}}{4} = 9\sqrt{3} \approx 15.59 cm². Oznacza to, że pole tego trójkąta wynosi około 15.59 centymetrów kwadratowych. Taka metoda jest niezwykle efektywna, gdyż pozwala na szybkie uzyskanie wyniku bez konieczności znajomości wysokości trójkąta.
Trójkąt prostokątny: jak wykorzystać kąty do obliczeń
Trójkąt prostokątny to inny typ trójkąta, w którym jeden z kątów wynosi 90 stopni. Aby obliczyć jego pole, wykorzystujemy wzór: P = \frac{1}{2} \cdot a \cdot b, gdzie a i b to długości boków, które tworzą kąt prosty. Ta metoda jest bardzo intuicyjna, ponieważ pole prostokątnego trójkąta można porównać do obliczania pola prostokąta, dzieląc je przez dwa.
Na przykład, jeśli mamy trójkąt prostokątny z długościami boków 4 cm i 3 cm, obliczamy pole w następujący sposób: P = \frac{1}{2} \cdot 4 \cdot 3 = \frac{12}{2} = 6 cm². To oznacza, że pole tego trójkąta wynosi 6 centymetrów kwadratowych. Taki sposób obliczeń jest szczególnie przydatny w praktyce, na przykład w budownictwie czy projektowaniu, gdzie często spotykamy się z kątami prostymi.
Trójkąt równoramienny: specyficzne wzory i ich zastosowanie
Trójkąt równoramienny to trójkąt, w którym dwa boki mają tę samą długość. Aby obliczyć jego pole, możemy skorzystać z wzoru, który jest podobny do tego stosowanego dla trójkątów ogólnie, ale uwzględnia specyfikę równoramiennych boków. W przypadku trójkąta równoramiennego, pole można obliczyć na podstawie długości boku oraz wysokości opuszczonej na podstawę. Wzór na pole trójkąta równoramiennego to: P = \frac{1}{2} \cdot a \cdot h, gdzie a to długość podstawy, a h to wysokość.Na przykład, rozważmy trójkąt równoramienny, w którym długość podstawy wynosi 8 cm, a wysokość 5 cm. Obliczamy pole w następujący sposób: P = \frac{1}{2} \cdot 8 \cdot 5 = 20 cm². To oznacza, że pole tego trójkąta wynosi 20 centymetrów kwadratowych. Dzięki tej metodzie można szybko i efektywnie obliczyć pole trójkąta równoramiennego, co jest przydatne w różnych zastosowaniach, takich jak projektowanie czy budownictwo.
Czytaj więcej: Symbol sumy w matematyce: jak poprawnie stosować notację sigma
Praktyczne przykłady obliczania pola trójkąta i ich zastosowania
Obliczanie pola trójkąta ma wiele praktycznych zastosowań w codziennym życiu. Na przykład, w architekturze często wykorzystuje się trójkąty do obliczeń powierzchni dachów, które mają kształt trójkątny. W takich przypadkach znajomość odpowiednich wzorów na pole trójkąta jest niezbędna do określenia ilości materiałów budowlanych potrzebnych do pokrycia dachu. Ponadto, w ogrodnictwie, obliczanie pola trójkąta może pomóc w planowaniu przestrzeni na rabaty kwiatowe czy trawniki.
Innym przykładem zastosowania obliczeń pola trójkąta jest projektowanie przestrzeni publicznych, takich jak parki czy place zabaw. Znajomość powierzchni, jaką zajmują różne elementy, pozwala na lepsze zaplanowanie układu i funkcjonalności przestrzeni. Dzięki tym praktycznym zastosowaniom, umiejętność obliczania pola trójkąta staje się nie tylko teoretyczną wiedzą, ale również cenną umiejętnością w wielu dziedzinach życia.
- Architektura: obliczanie powierzchni dachów trójkątnych.
- Ogród: planowanie rabat kwiatowych w kształcie trójkąta.
- Projektowanie przestrzeni publicznych: optymalizacja układów parków i placów zabaw.
Przykłady z życia codziennego: kiedy potrzebujemy obliczeń
Obliczanie pola trójkąta jest niezwykle przydatne w wielu codziennych sytuacjach. Na przykład, architekci często muszą obliczać powierzchnię trójkątnych dachów, aby dokładnie oszacować ilość materiałów potrzebnych do budowy. W ogrodnictwie, obliczanie pola trójkąta może być użyteczne przy planowaniu rabat kwiatowych czy układów ścieżek, co pozwala na efektywne wykorzystanie przestrzeni. Ponadto, w edukacji, nauczyciele mogą wykorzystywać te obliczenia do nauki geometrii w praktyczny sposób, co pomaga uczniom lepiej zrozumieć temat.
Ćwiczenia do samodzielnego rozwiązania: sprawdź swoje umiejętności
Aby skutecznie przyswoić wiedzę na temat obliczania pola trójkąta, warto regularnie ćwiczyć. Przygotowaliśmy kilka praktycznych zadań, które pomogą w utrwaleniu umiejętności. Na przykład, oblicz pole trójkąta o bokach 5 cm, 12 cm i 13 cm, oraz pole trójkąta równobocznego o boku 10 cm. Takie ćwiczenia pozwalają na samodzielne sprawdzenie wiedzy i umiejętności, a także na lepsze zrozumienie zastosowań wzorów w praktyce.
Jak wykorzystać obliczenia pola trójkąta w projektowaniu 3D
W dzisiejszych czasach, obliczanie pola trójkąta ma ogromne znaczenie nie tylko w tradycyjnych dziedzinach, takich jak architektura czy ogrodnictwo, ale także w nowoczesnym projektowaniu 3D. W programach do modelowania 3D, takich jak AutoCAD czy SketchUp, umiejętność precyzyjnego obliczania pól trójkątów jest kluczowa do tworzenia skomplikowanych struktur i form. Dzięki tym obliczeniom, projektanci mogą lepiej planować przestrzeń, optymalizować materiały oraz przewidywać koszty, co jest istotne w kontekście zrównoważonego rozwoju i efektywności kosztowej.
Co więcej, w kontekście technologii druku 3D, zrozumienie geometrii trójkątów może pomóc w tworzeniu bardziej zaawansowanych modeli, które są zarówno estetyczne, jak i funkcjonalne. Wykorzystując algorytmy, które bazują na obliczeniach pola trójkąta, projektanci mogą generować unikalne kształty, które są zoptymalizowane pod kątem wytrzymałości i wagi. W przyszłości, w miarę rozwoju technologii, umiejętność ta stanie się jeszcze bardziej istotna, a jej zastosowanie w różnych branżach może przynieść znaczące oszczędności i innowacje.