Teoria potrzebna do zadania:
Wykres funkcji y=sin x
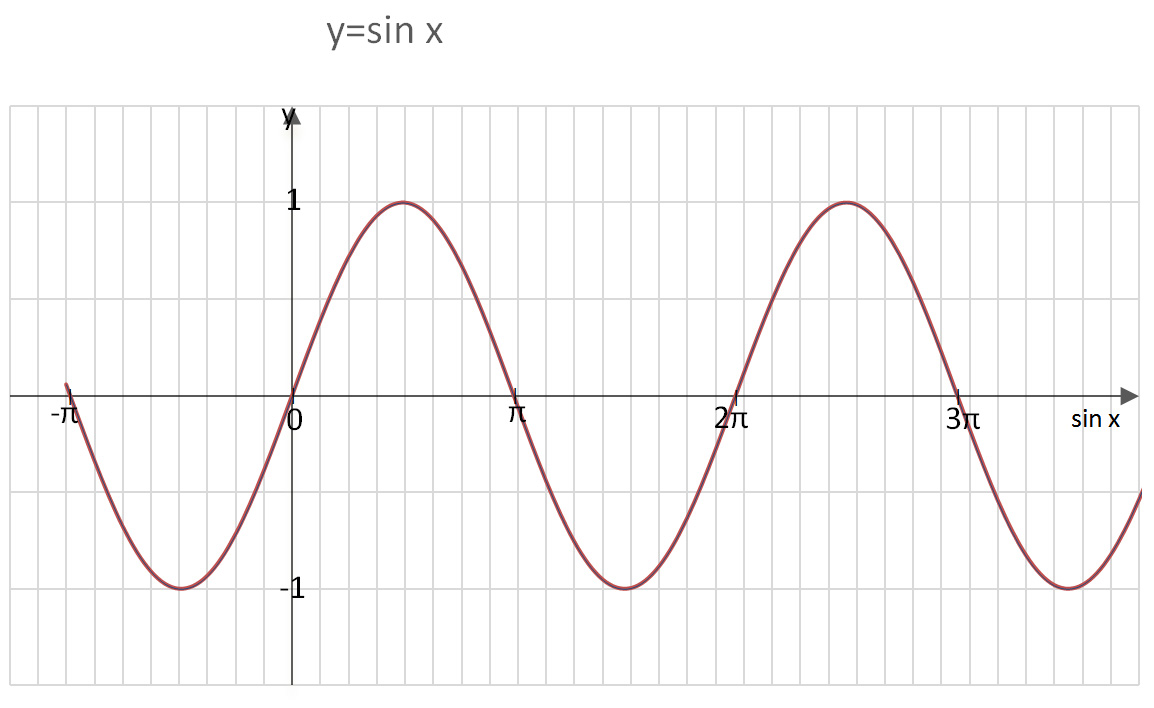
Zadanie:
Zadanie:Rozwiąż równanie sin(2x – 4π/3) =-√3/2Rozwiązanie:
W pierwszej kolejności sprawdzamy dla jakich x funkcja trygonometryczna sinx jest równa√3/2.
Z tablic trygonometrycznych odczytujemy, że sinx =√3/2 dla x =π/3. Tyle, że nas interesuje kiedy sinx =-√3/2
Popatrzmy na wykres:
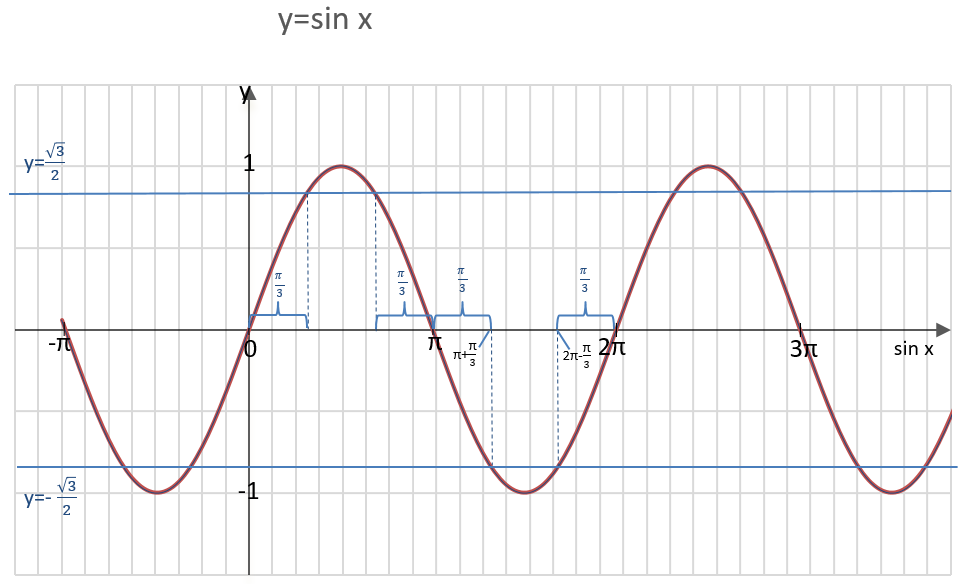
Z wykresu wynika, że sinx =-√3/2 dla x = π + π/3 oraz dla x = 2π – π/3
Pamiętając o tym, że okres funkcji sinus wynosi 2π mamy:
$$sinx = \frac{-\sqrt3}2, \textrm{dla x}=π +\fracπ3 + \textrm{2kπ lub x}=2π – \fracπ3 + \textrm{2kπ, k∈C}$$
Zapis k∈C oznacza, że zamiast k możesz wstawić dowolną liczbę całkowitą
Wracamy do naszego równania: sin(2x – 4π/3) =-√3/2
Zamiast -√3/2 podstawiamy wynik z punktu 2 i mamy dwa równania:
$$\textrm{sin(2x} – \frac{4π}3) =\textrm{sin(π+}\fracπ3 + \textrm{2kπ) lub sin(2x} – \frac{4π}3)=\textrm{sin(}2π – \fracπ3 + \textrm{2kπ), k∈C}$$
„Opuszczamy” funkcję sinus i mamy:
$$\textrm{2x} – \frac{4π}3 =\textrm{π+}\fracπ3 + \textrm{2kπ lub 2x} – \frac{4π}3=\textrm{}2π – \fracπ3 + \textrm{2kπ, k∈C}$$
Wyliczamy x przenosząc -4π/3 na drugą stronę równania i dzieląc wszystko przez 2
Pamiętajmy o zmianie znaku przy przenoszeniu liczby na drugą stronę równania. Dzielenie przez 2 to to samo co mnożenie przez 1/2
$$\textrm{2x} =\textrm{π+}\fracπ3 + \frac{4π}3+ \textrm{2kπ lub 2x} =\textrm{}2π – \fracπ3 + \frac{4π}3+ \textrm{2kπ, k∈C}$$
$$\textrm{2x} =\frac{3π}3 + \fracπ3 + \frac{4π}3+ \textrm{2kπ lub 2x} =\frac{6π}3 – \fracπ3 + \frac{4π}3+ \textrm{2kπ, k∈C}$$
$$\textrm{2x} =\frac{8π}3 + \textrm{2kπ lub 2x} =\frac{9π}3+ \textrm{2kπ, k∈C} /:2$$
$$\textrm{x} =\frac{8π}6 + \textrm{kπ lub x} =\frac{9π}6+ \textrm{kπ, k∈C} $$
Skracamy jeszcze powstałe ułamki i mamy wynik:
$$\textrm{x} =\frac{4π}3 + \textrm{kπ lub x} =\frac{3π}2+ \textrm{kπ, k∈C} $$